t-SNE算法解析与简单代码实现
t-SNE算法解析与简单代码实现
-
- t-SNE
-
- SNE基本原理和介绍
- SNE原理推导
- t-SNE的引入
-
- Symmetric SNE
- 拥挤现象
- 关于 σ \sigma σ的求法
- 代码解析
-
- 参数说明
- Reference
t-SNE
t-SNE感觉就是将两个数据点的相似度转换为实际距离的算法
t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法,是由 Laurens van der Maaten 和 Geoffrey Hinton在08年提出来。此外,t-SNE 是一种非线性降维算法,非常适用于**高维数据降维到2维或者3维**,进行可视化。
t-SNE是由SNE(Stochastic Neighbor Embedding, SNE; Hinton and Roweis, 2002)发展而来。我们先介绍SNE的基本原理,之后再扩展到t-SNE。
SNE基本原理和介绍
SNE是通过仿射(affinitie)变换将数据点映射到概率分布上,主要包括两个步骤:
- SNE构建一个高维对象之间的概率分布,使得相似的对象有更高的概率被选择,而不相似的对象有较低的概率被选择。
- SNE在低维空间里在构建这些点的概率分布,使得这两个概率分布之间尽可能的相似。
我们看到t-SNE模型是非监督的降维,他跟k-means等不同,他不能通过训练得到一些东西之后再用于其它数据(比如k-means可以通过训练得到k个点,再用于其它数据集,而t-SNE只能单独的对数据做操作,也就是说用k-means训练好的模型我们可以直接用于其他数据集来得到正确的分类结果,但是t-SNE只能在单独一个数据集中使用,如果换数据集就需要重新训练。
SNE原理推导
SNE是先将欧几里得距离转换为条件概率来表达点与点之间的相似度。具体来说,给定一个N个高维的数据 x 1 , . . . , x N x_1,...,x_N x1,...,xN(注意N不是维度),SNE首先计算概率 p i j p_{ij} pij,正比于 x i x_i xi和 x j x_j xj之间的相似度。
p j ∣ i = exp ( − ∥ x i − x j ∥ 2 / ( 2 σ i 2 ) ) ∑ k ≠ i exp ( − ∥ x i − x k ∥ 2 / ( 2 σ i 2 ) ) p_{j \mid i}=\frac{\exp \left(-\left\|x_{i}-x_{j}\right\|^{2} /\left(2 \sigma_{i}^{2}\right)\right)}{\sum_{k \neq i} \exp \left(-\left\|x_{i}-x_{k}\right\|^{2} /\left(2 \sigma_{i}^{2}\right)\right)} pj∣i=∑k=iexp(−∥xi−xk∥2/(2σi2))exp(−∥xi−xj∥2/(2σi2))
这里的有一个参数是 σ i \sigma_i σi,对于不同的点 x i x_i xi取值不一样,后续会讨论如何设置。此外设置 p x ∣ x = 0 p_{x|x}=0 px∣x=0,因为我们关注的是两两之间的相似度。等式的分母是数据集中所有的点到 x i x_i xi的距离之和,因此这个式子和softmax公式很相似,结果都是概率,等式的分子相当于一个高斯分布, σ \sigma σ就是方差, μ \mu μ其实就是 x j x_j xj。
那对于低维度下的 y i y_i yi,我们可以指定高斯分布为方差为 1 2 \frac{1}{\sqrt2} 21,因此它们之间的相似度如下:
q j ∣ i = exp ( − ∥ x i − x j ∥ 2 ) ∑ k ≠ i exp ( − ∥ x i − x k ∥ 2 ) q_{j \mid i}=\frac{\exp \left(-\left\|x_{i}-x_{j}\right\|^{2}\right)}{\sum_{k \neq i} \exp \left(-\left\|x_{i}-x_{k}\right\|^{2}\right)} qj∣i=∑k=iexp(−∥xi−xk∥2)exp(−∥xi−xj∥2)
同样的 q i ∣ i = 0 q_{i|i}=0 qi∣i=0
如果降维的效果比较好,局部特征保留完整,那么 p i ∣ j = q i ∣ j p_{i|j}=q_{i|j} pi∣j=qi∣j , 因此我们优化两个分布之间的距离-KL散度(Kullback-Leibler divergences),那么目标函数(cost function)如下:
C = ∑ i K L ( P i ∥ Q i ) = ∑ i ∑ j p j ∣ i log p j ∣ i q j ∣ i C=\sum_{i} K L\left(P_{i} \| Q_{i}\right)=\sum_{i} \sum_{j} p_{j \mid i} \log \frac{p_{j \mid i}}{q_{j \mid i}} C=i∑KL(Pi∥Qi)=i∑j∑pj∣ilogqj∣ipj∣i
这里的 P i P_i Pi表示了给定点 x i x_i xi下,其他所有数据点的条件概率分布。需要注意的是KL散度具有不对称性
这里的不对称性我看到有两种解释:
-
我们都知道 p j ∣ i p_{j|i} pj∣i代表的是j到i的距离, p i ∣ j p_{i|j} pi∣j代表的是i到j的距离,按照常识来说这两个距离应该是相等的,但是在我们带入上面的公式很容易发现他们的分母并不是相等的, p j ∣ i p_{j|i} pj∣i的分母中有 − ∣ ∣ x i − x k ∣ ∣ 2 -||x_i-x_k||^2 −∣∣xi−xk∣∣2,但是 p i ∣ j p_{i|j} pi∣j的分母中则是 − ∣ ∣ x j − x k ∣ ∣ 2 -||x_j-x_k||^2 −∣∣xj−xk∣∣2。
-
在低维映射中不同的距离对应的惩罚权重是不同的,具体来说:距离较远的两个点来表达距离较近的两个点会产生更大的cost,相反,用较近的两个点来表达较远的两个点产生的cost相对较小(注意:类似于回归容易受异常值影响,但效果相反)。即用较小的 q j ∣ i = 0.2 q_{j|i}=0.2 qj∣i=0.2来建模较大的 p j ∣ i = 0.8 p_{j|i}=0.8 pj∣i=0.8, c o s t = p l o g ( p q ) = 1.11 cost=plog(\frac{p}{q})=1.11 cost=plog(qp)=1.11,同样用较大的 q j ∣ i = 0.8 q_{j|i}=0.8 qj∣i=0.8来建模较大的 p j ∣ i = 0.2 p_{j|i}=0.2 pj∣i=0.2, cost=-0.277, 因此,SNE会倾向于保留数据中的局部特征
t-SNE的引入
尽管SNE提供了很好的可视化方法,但是他很难优化,而且存在”crowding problem”(拥挤问题)。后续中,Hinton等人又提出了t-SNE的方法。与SNE不同,主要如下:
- 使用对称版的SNE,简化梯度公式
- 低维空间下,使用t分布替代高斯分布表达两点之间的相似度
Symmetric SNE
优化 p i ∣ j p_{i\mid j} pi∣j和 q i ∣ j q_{i\mid j} qi∣j的KL散度的一种替换思路是,使用联合概率分布来替换条件概率分布,即P是高维空间里各个点的联合概率分布,Q是低维空间下的,目标函数为:
C = K L ( P ∥ Q ) = ∑ i ∑ j p i j log p i j q i j C=K L(P \| Q)=\sum_{i} \sum_{j} p_{i j} \log \frac{p_{i j}}{q_{i j}} C=KL(P∥Q)=i∑j∑pijlogqijpij
概率分布改写为:
p i j = exp ( − ∥ x i − x j ∥ 2 / 2 σ 2 ) ∑ k ≠ l exp ( − ∥ x k − x l ∥ 2 / 2 σ 2 ) q i j = exp ( − ∥ y i − y j ∥ 2 ) ∑ k ≠ l exp ( − ∥ y k − y l ∥ 2 ) p_{i j}=\frac{\exp \left(-\left\|x_{i}-x_{j}\right\|^{2} / 2 \sigma^{2}\right)}{\sum_{k \neq l} \exp \left(-\left\|x_{k}-x_{l}\right\|^{2} / 2 \sigma^{2}\right)} \quad q_{i j}=\frac{\exp \left(-\left\|y_{i}-y_{j}\right\|^{2}\right)}{\sum_{k \neq l} \exp \left(-\left\|y_{k}-y l\right\|^{2}\right)} pij=∑k=lexp(−∥xk−xl∥2/2σ2)exp(−∥xi−xj∥2/2σ2)qij=∑k=lexp(−∥yk−yl∥2)exp(−∥yi−yj∥2)
这里可以看到如果用联合分布替换条件分布后,分母就能保持一致了,不论是 p i j p_{ij} pij还是 p j i p_{ji} pji他们的分母都是一样的,消除了SNE的不对称性 。
具体实现如下:
- 先根据条件概率求出联合概率 p i j p_{ij} pij,这个式子保证了对称性
p i j = p i ∣ j + p j ∣ i p_{i j}=p_{i \mid j}+p_{j \mid i} pij=pi∣j+pj∣i
- 将得到的联合概率再除以其他所有的联合概率,保证了归一化
p i j = p i j ∑ i ∑ j p i j p_{i j}=\frac{p_{i j}}{\sum_{i} \sum_{j} p_{i j}} pij=∑i∑jpijpij
拥挤现象
对称的SNE容易产生拥挤现象,数据从高维到低维进行转换的过程中会出现在高维上分得开的数据映射到低维上,距离变得非常小并且不同簇拥挤在一起。
那么怎么解决这个问题呢?我们需要将相似的点的距离缩小,不相似的点的距离变大
为了解决这个问题,我们使用student-t分布给低维的数据进行建模。
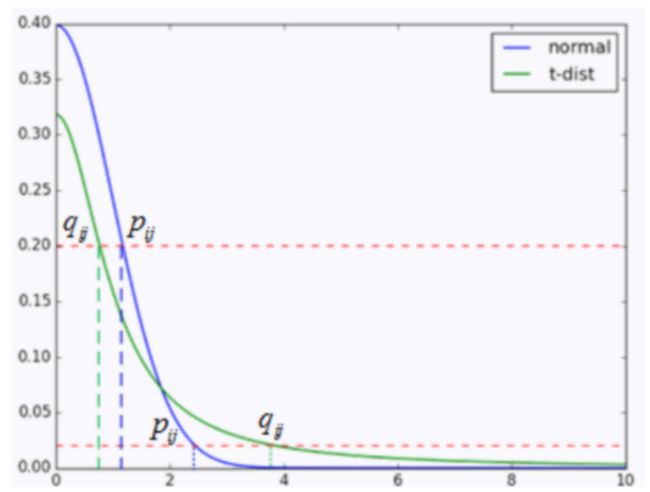
如上面的图所示,横坐标是距离,纵坐标是概率(两点的相似度)。
蓝色表示的是高维数据的高斯分布的曲线,绿色的是低维的t分布的曲线,首先看上面两个点 q i j , p i j q_{ij},p_{ij} qij,pij,p是0.2概率下在高维空间的距离,q是低维空间下0.2概率的距离,模型训练其实就是用p去接近q,因此模型在训练的时候,从高维映射到低维数据时,距离会减小。而对于**下面两个点p和q(概率好像为0.02,这个概率非常小了,说明i和j不相似),从p映射到q时,距离则会增大。上面已经介绍过了,p和q实际上就是两点的相似度。**通过学生t分布,我们就能实现,从高维映射到低维后,相似的点距离缩小,不相似的点距离变大了。
所以更改公式为:
q i j = ( 1 + ∥ y i − y j ∥ 2 ) − 1 ∑ k ≠ l ( 1 + ∥ y k − y l ∥ 2 ) − 1 q_{i j}=\frac{\left(1+\left\|y_{i}-y_{j}\right\|^{2}\right)^{-1}}{\sum_{k \neq l}\left(1+\left\|y_{k}-y_{l}\right\|^{2}\right)^{-1}} qij=∑k=l(1+∥yk−yl∥2)−1(1+∥yi−yj∥2)−1
t-SNE的一般步骤:
计算 p i ∣ j p_{i \mid j} pi∣j和 p j ∣ i p_{j \mid i} pj∣i
p j ∣ i = exp ( − ∥ x i − x j ∥ 2 / ( 2 σ i 2 ) ) ∑ k ≠ i exp ( − ∥ x i − x k ∥ 2 / ( 2 σ i 2 ) ) p_{j \mid i}=\frac{\exp \left(-\left\|x_{i}-x_{j}\right\|^{2} /\left(2 \sigma_{i}^{2}\right)\right)}{\sum_{k \neq i} \exp \left(-\left\|x_{i}-x_{k}\right\|^{2} /\left(2 \sigma_{i}^{2}\right)\right)} pj∣i=∑k=iexp(−∥xi−xk∥2/(2σi2))exp(−∥xi−xj∥2/(2σi2))
利用上面的结果计算 p i j p_{i j} pij
p i j = p i ∣ j + p j ∣ i p i j = p i j ∑ i ∑ j p i j p_{i j}=p_{i \mid j}+p_{j \mid i} \qquad \quad p_{i j}=\frac{p_{i j}}{\sum_{i} \sum_{j} p_{i j}} pij=pi∣j+pj∣ipij=∑i∑jpijpij
随机生成低维随机数分布:
q i j = ( 1 + ∥ y i − y j ∥ 2 ) − 1 ∑ k ≠ l ( 1 + ∥ y k − y l ∥ 2 ) − 1 q_{i j}=\frac{\left(1+\left\|y_{i}-y_{j}\right\|^{2}\right)^{-1}}{\sum_{k \neq l}\left(1+\left\|y_{k}-y_{l}\right\|^{2}\right)^{-1}} qij=∑k=l(1+∥yk−yl∥2)−1(1+∥yi−yj∥2)−1
利用梯度下降,另C最小:
C = K L ( P ∥ Q ) = ∑ i ∑ j p i j log p i j q i j C=K L(P \| Q)=\sum_{i} \sum_{j} p_{i j} \log \frac{p_{i j}}{q_{i j}} C=KL(P∥Q)=i∑j∑pijlogqijpij
梯度公式为:
δ C δ y i = 4 ∑ j ( p i j − q i j ) ( y i − y j ) ( 1 + ∥ y i − y j ∥ 2 ) − 1 \frac{\delta C}{\delta y_{i}}=4 \sum_{j}\left(p_{i j}-q_{i j}\right)\left(y_{i}-y_{j}\right)\left(1+\left\|y_{i}-y_{j}\right\|^{2}\right)^{-1} δyiδC=4j∑(pij−qij)(yi−yj)(1+∥yi−yj∥2)−1
关于 σ \sigma σ的求法
我们都知道公式为:
p j ∣ i = exp ( − ∥ x i − x j ∥ 2 / ( 2 σ i 2 ) ) ∑ k ≠ i exp ( − ∥ x i − x k ∥ 2 / ( 2 σ i 2 ) ) p_{j \mid i}=\frac{\exp \left(-\left\|x_{i}-x_{j}\right\|^{2} /\left(2 \sigma_{i}^{2}\right)\right)}{\sum_{k \neq i} \exp \left(-\left\|x_{i}-x_{k}\right\|^{2} /\left(2 \sigma_{i}^{2}\right)\right)} pj∣i=∑k=iexp(−∥xi−xk∥2/(2σi2))exp(−∥xi−xj∥2/(2σi2))
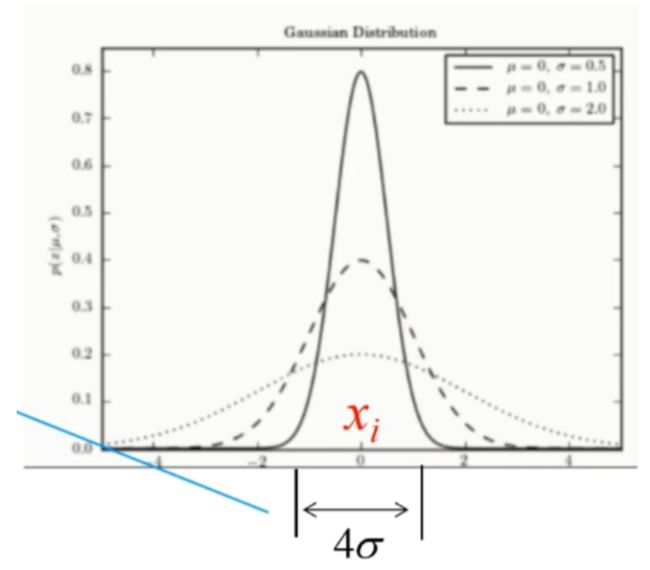
公式上面的部分可以看作一个高斯分布, x i x_i xi对应了高斯分布中的 μ \mu μ, σ \sigma σ控制图像的宽度
因为距离 x i x_i xi小于 2 σ 2 \sigma 2σ的点对P的计算起到了决定性的作用。因此我们可以根据 σ \sigma σ的取值来控制这些点的数量。
- 当 x i x_i xi附近的临近点较多时,我们减小 σ \sigma σ以此来减少临近点
- 当 x i x_i xi附近的临近点较少时,我们增大 σ \sigma σ以此来增加临近点
我们保证 x i x_i xi附近的临近点尽可能的一致,有点类似于KNN,而t-SNE的stochastic neighbor随机近邻就有这个意思
定义一个困惑值(perplexity),用二分搜索的方式来寻找一个最佳的 σ \sigma σ。其中困惑度指:
Perp ( P i ) = 2 H ( P i ) \operatorname{Perp}\left(P_{i}\right)=2^{H\left(P_{i}\right)} Perp(Pi)=2H(Pi)
这里的 H ( P i ) H(P_i) H(Pi)是 P i P_i Pi的熵,即:
H ( P i ) = − ∑ j p j ∣ i log 2 p j ∣ i H\left(P_{i}\right)=-\sum_{j} p_{j \mid i} \log _{2} p_{j \mid i} H(Pi)=−j∑pj∣ilog2pj∣i
整理以后可以写为:
log ( P e r p ) = − ∑ j p j ∣ i log ( p j ∣ i ) \log (\mathrm{Perp})=-\sum_{j} p_{j \mid i} \log \left(p_{j \mid i}\right) log(Perp)=−j∑pj∣ilog(pj∣i)
个人理解补充:
上面的公式可以拆开来写为:
log ( P e r p ) = − ( ∑ j p j ∣ i ∑ j log ( p j ∣ i ) ) \log (\mathrm{Perp})=-\left(\sum_{j} p_{j \mid i} \sum_{j}\log \left(p_{j \mid i}\right)\right) log(Perp)=−(j∑pj∣ij∑log(pj∣i))
而 ∑ j p j ∣ i \sum_{j} p_{j \mid i} ∑jpj∣i 的值则为1那么公式就变为:
log ( P e r p ) = − ∑ j log ( p j ∣ i ) \log (\mathrm{Perp})=- \sum_{j}\log \left(p_{j \mid i}\right) log(Perp)=−j∑log(pj∣i)
把log去掉可以简单写为:
P e r p = − ∑ j p j ∣ i \mathrm{Perp}=- \sum_{j} p_{j \mid i} Perp=−j∑pj∣i
因此我们可以把困惑度可以解释为一个点附近的有效近邻点个数(我水平有限,不知道怎么解释,欢迎大家讨论 //笑哭)困惑值一般选择5-50之间,表示的是聚类出来之后,每个集群的大小。例如设perplexity为2,那么就很有可能得到很多两个一对的小集群。
在上面的介绍中,我们得到了如下的式子,并且知道Perp的取值一般在5-50之间,所以我们就可以使用二分法去得到合适的 σ i \sigma_i σi了
log ( P e r p ) = − ∑ j p j ∣ i log ( p j ∣ i ) \log (\mathrm{Perp})=-\sum_{j} p_{j \mid i} \log \left(p_{j \mid i}\right) log(Perp)=−j∑pj∣ilog(pj∣i)
代码解析
使用sklearn库
参数说明
| parameters | description |
|---|---|
| n_components | int, 默认为2,嵌入空间的维度(嵌入空间的意思就是结果空间) |
| perplexity(困惑值) | float, 默认为30,数据集越大,需要参数值越大,建议值位5-50 |
| early_exaggeration | float, 默认为12.0,控制原始空间中的自然集群在嵌入式空间中的紧密程度以及它们之间的空间。 对于较大的值,嵌入式空间中自然群集之间的空间将更大。 再次,这个参数的选择不是很关键。 如果在初始优化期间成本函数增加,则可能是该参数值过高。 |
| learning_rate | float, default:200.0, 学习率,建议取值为10.0-1000.0 |
| n_iter | int, default:1000, 最大迭代次数 |
| n_iter_without_progress | int, default:300, 另一种形式的最大迭代次数,必须是50的倍数 |
| min_grad_norm | float, default:1e-7, 如果梯度低于该值,则停止算法 |
| metric | string or callable, 精确度的计量方式 |
| init | string or numpy array, default:”random”, 可以是’random’, ‘pca’或者一个numpy数组(shape=(n_samples, n_components)。 |
| verbose | int, default:0, 训练过程是否可视 |
| random_state | int, RandomState instance or None, default:None,控制随机数的生成 |
| method | string, default:’barnes_hut’, 对于大数据集用默认值,对于小数据集用’exact’ |
| angle | float, default:0.5, 只有method='barnes_hut'时可用 |
首先生成一堆原始数据
import matplotlib.pyplot as plt
from sklearn import manifold, datasets
"""对S型曲线数据的降维和可视化"""
# 生成1000个S型曲线数据
x, color = datasets.make_s_curve(n_samples=1000, random_state=0) # x是[1000,2]的2维数据,color是[1000,1]的一维数据
n_neighbors = 10
n_components = 2
# 创建自定义图像
fig = plt.figure(figsize=(15, 15)) # 指定图像的宽和高
plt.suptitle("Dimensionality Reduction and Visualization of S-Curve Data ", fontsize=14) # 自定义图像名称
# 绘制S型曲线的3D图像
ax = fig.add_subplot(211, projection='3d') # 创建子图
ax.scatter(x[:, 0], x[:, 1], x[:, 2], c=color, cmap=plt.cm.Spectral) # 绘制散点图,为不同标签的点赋予不同的颜色
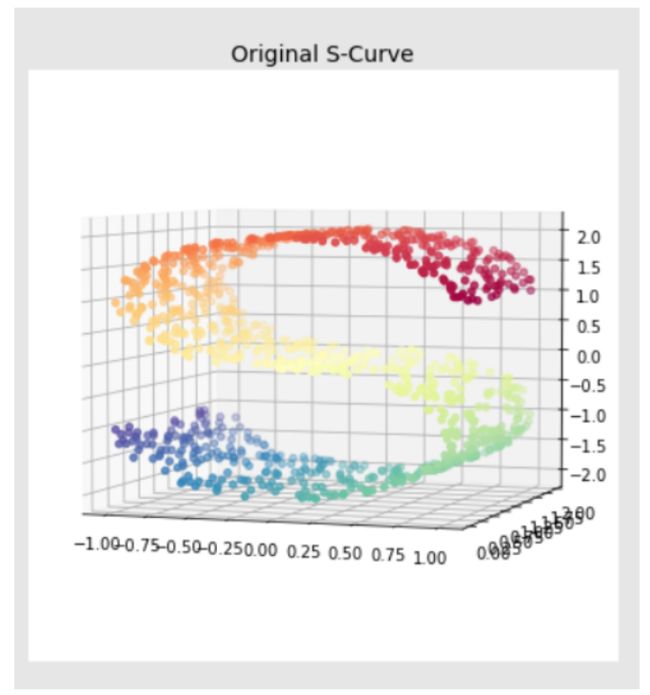
ax.set_title('Original S-Curve', fontsize=14)
ax.view_init(4, -72) # 初始化视角
# t-SNE的降维与可视化
ts = manifold.TSNE(n_components=n_components,perplexity=30)
# 训练模型
y = ts.fit_transform(x)
ax1 = fig.add_subplot(2, 1, 2)
plt.scatter(y[:, 0], y[:, 1], c=color, cmap=plt.cm.Spectral)
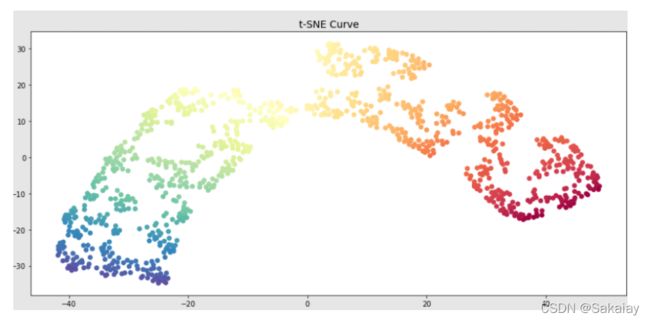
ax1.set_title('t-SNE Curve', fontsize=14)
plt.show()
Reference
http://www.datakit.cn/blog/2017/02/05/t_sne_full.html
https://www.bilibili.com/video/BV1cU4y1w74A?from=search&seid=12192893821701173088&spm_id_from=333.337.0.0
http://bindog.github.io/blog/2018/07/31/t-sne-tips/
https://towardsdatascience.com/t-sne-python-example-1ded9953f26
https://blog.csdn.net/hustqb/article/details/78144384