SVM模型

Python中提供了有关线性可分SVM或近似线性可分SVM的实现功能，只需要导入sklearn模块，并调用svm子模块中的LinearSVC类即可

LinearSVC(penalty='l2', loss='squared_hinge', dual=True, tol=0.0001, C=1.0,
	multi_class='ovr', fit_intercept=True, intercept_scaling=1,
	class_weight=None, verbose=0, random_state=None, max_iter=1000)
	
penalty：用于指定一范式或二范式的惩罚项，默认为二范式。

loss：用于指定某种损失函数，可以是合页损失函数（'hinge'），也可以是合页损失函数的平方（'squared_hinge'），后者是该参数的默认值。

dual：bool类型参数，是否对目标函数做对偶性转换，默认为True，即建模时需要利用拉格朗日函数的对偶性；但样本量超过变量个数时，该参数优先选择False。
tol：用于指定SVM模型迭代的收敛条件，默认为0.0001。

C：用于指定目标函数中松弛因子的惩罚系数值，默认为1。

multi_class：当因变量为多分类问题时，用于指定算法的分类策略。如为'ovr'，表示采用one-vs-rest策略；如果为'crammer_singer'，表示联合分类策略，尽管该策略具有更好的准确率，但是其运算过程将花费更多的时间。

fit_intercept：bool类型参数，是否拟合线性“超平面”的截距项，默认为True。

intercept_scaling：当参数fit_intercept为True时，该参数有效，通过给参数传递一个浮点值，就相当于在自变量X矩阵中添加一常数列，默认该参数值为1。

class_weight：用于指定因变量类别的权重，如果为字典，则通过字典的形式
{class_label:weight}传递每个类别的权重；如果为字符串'balanced'，则每个分类的权重与实际样本中的比例成反比，当各分类存在严重不平衡时，设置为'balanced'会比较好；如果为None，则表示每个分类的权重相等。

verbose：bool类型参数，是否输出模型迭代过程的信息，默认为0，表示不输出。

random_state：用于指定随机数生成器的种子。

max_iter：指定模型求解过程中的最大迭代次数，默认为1000。

在实际应用中，SVM模型对核函数的选择是非常敏感的，所以需要通过先验的领域知识或者交叉验证的方法选出合理的核函数。大多数情况下，选择
高斯核函数是一种相对偷懒而有效的方法，因为高斯核是一种指数函数，它的泰勒展开式可以是无穷维的，即相当于把原始样本点映射到高维空间中。

关于非线性可分SVM模型的功能实现，可以利用Python中的sklearn模块，可以通过调用svm子模块中的SVC类轻松搞定。接下来介绍一下该“类”的语法和参数含义：

SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True,
	probability=False, tol=0.001, cache_size=200, class_weight=None,
	verbose=False, max_iter=-1, decision_function_shape='ovr', random_state=None)
	
C：用于指定目标函数中松弛因子的惩罚系数值，默认为1。kernel：用于指定SVM模型的核函数，该参数如果为'linear'，就表示线性核函数；如果为'poly'，就表示多项式核函数，核函数中的r和p值分别使用degree参数和gamma参数指定；如果为'rbf'，表示径向基核函数，核函数中的r参数值仍然通过gamma参数指定；如果
为'sigmoid'，表示Sigmoid核函数，核函数中的r参数值需要通过gamma参数指定；如果为'precomputed'，表示计算一个核矩阵。

degree：用于指定多项式核函数中的p参数值。

gamma：用于指定多项式核函数或径向基核函数或Sigmoid核函数中的r参数值。

coef0：用于指定多项式核函数或Sigmoid核函数中的r参数值。

shrinking：bool类型参数，是否采用启发式收缩方式，默认为True。

probability：bool类型参数，是否需要对样本所属类别进行概率计算，默认为False。

tol：用于指定SVM模型迭代的收敛条件，默认为0.001。

cache_size：用于指定核函数运算的内存空间，默认为200M。

class_weight：用于指定因变量类别的权重，如果为字典，则通过字典的形式
{class_label:weight}传递每个类别的权重；如果为字符串'balanced'，则每个分类的权重与实际样本中的比例成反比，当各分类存在严重不平衡时，设置为'balanced'会比较好；如果为None，则表示每个分类的权重相等。

verbose：bool类型参数，是否输出模型迭代过程的信息，默认为0，表示不输出。

max_iter：指定模型求解过程中的最大迭代次数，默认为-1，表示不限制迭代次数。

decision_function_shape：用于指定SVM模型的决策函数形状，如果为'ovo'，即one-vs-one的分类策略，则决策函数形状的形状为[样本数量,类别个数*(类别个数-1)/2]；如果为'ovr'，即one-vs-rest的分类策略，则决策函数形状的形状为[样本数量,类别个数]；默认为None，在sklearn版本为0.18及以上时，None值对应的默认选项为'ovr'。

random_state：用于指定随机数生成器的种子。

SVM模型不仅可以解决分类问题，还可以用来解决连续数据的预测问题。相比于传统的线性回归，它具有几项优点，例如模型对数据的分布没有任何约束、模型不受多重共线性的影响、模型受异常点的影响力度远小于线性回归。
不论是线性SVM回归还是非线性SVM回归，都可以借助于Python的sklearn模块完成落地，只需调用svm子模块中的LinearSVR以及SVR类就可以轻松实现算法的运算。

svm.LinearSVR(epsilon=0.0, tol=0.0001, C=1.0, loss='epsilon_insensitive',
	fit_intercept=True, intercept_scaling=1.0 ,dual=True,
	verbose=0, random_state=None, max_iter=1000)

svm.SVR(kernel='rbf', degree=3, gamma='auto', coef0=0.0, tol=0.001,C=10.,
	epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=-1)


epsilon：用于指定损失函数中的r值，在线性SVR中默认为0，在非线性SVR中默认为0.1。

tol：用于指定SVM模型迭代的收敛条件，在线性SVR中默认为0.0001，在非线性SVR中默认为0.001。

C：用于指定目标函数中松弛因子的惩罚系数值，默认为1。

loss：用于指定线性SVR的损失函数，如果为'epsilon_insensitive'，则表示使用|yi-f(xi)|-ξ(∗)≤ε的损失判断；如果为'squared_epsilon_insensitive'则表示使用(yi-f(xi))2-ξ(∗)≤ε的损失判断。

fit_intercept：bool类型参数，是否拟合线性SVR的截距项，默认为True。

intercept_scaling：当参数fit_intercept为True时，该参数有效，通过给参数传递一个浮点值，就相当于在自变量X矩阵中添加一常数列，默认该参数值为1。

dual：bool类型参数，是否对目标函数做对偶性转换，默认为True，即建模时需要利用拉格朗日函数的对偶性；但样本量超过变量个数时，该参数优先选择False。

verbose：bool类型参数，是否输出模型迭代过程的信息，默认为0，表示不输出。

random_state：用于指定随机数生成器的种子。

max_iter：指定模型求解过程中的最大迭代次数，在线性SVR中默认为1000，在非线性SVR中默认为-1。

kernel：用于指定常用的核函数，如径向基核函数、多项式核函数、Sigmoid核函数和线性核函数。

degree：用于指定多项式核函数中的p参数值。

gamma：用于指定多项式核函数或径向基核函数或Sigmoid核函数中的γ参数值。

coef0：用于指定多项式核函数或Sigmoid核函数中的r参数值。

shrinking：bool类型参数，是否采用启发式收缩方式，默认为True。

cache_size：用于指定核函数运算的内存空间，默认为200M。

分类问题的解决

本节所使用的数据集是关于手体字母的识别，当一个用户在设备中写入某个字母后，该设备就需要准确地识别并返回写入字母的实际值。很显然，这是一个分类问题，即根据写入字母的特征信息（如字母的宽度、高度、边际等）去判断其属于哪一种字母。该数据集一共包含20000个观测和17个变量，其中变量letter为因变量，具体的值就是20个英文字母。接下来利用
SVM模型对该数据集的因变量做分类判断。
v首先使用线性可分SVM对手体字母数据集建模，由于该模型会受到惩罚系数C的影响，故应用交叉验证的方法，从给定的几种C值中筛选出一个相对合理的

# 导入第三方模块
from sklearn import svm
import pandas as pd
from sklearn import model_selection
from sklearn import metrics

# 读取外部数据
letters = pd.read_csv(r'letterdata.csv')
# 数据前5行
letters.head()


out:
	letter	xbox	ybox	width	height	onpix	xbar	ybar	x2bar	y2bar	xybar	x2ybar	xy2bar	xedge	xedgey	yedge	yedgex
0	T		2	8	3	5	1	8	13	0	6	6	10	8	0	8	0	8
1	I		5	12	3	7	2	10	5	5	4	13	3	9	2	8	4	10
2	D		4	11	6	8	6	10	6	2	6	10	3	7	3	7	3	9
3	N		7	11	6	6	3	5	9	4	6	4	4	10	6	10	2	8
4	G		2	1	3	1	1	8	6	6	6	6	5	9	1	7	5	10

# 将数据拆分为训练集和测试集
predictors = letters.columns[1:]
X_train,X_test,y_train,y_test = model_selection.train_test_split(letters[predictors], letters.letter, 
                                                                 test_size = 0.25, random_state = 1234)

# 使用网格搜索法，选择线性可分SVM“类”中的最佳C值
C=[0.05,0.1,0.5,1,2,5]
parameters = {'C':C}
grid_linear_svc = model_selection.GridSearchCV(estimator = svm.LinearSVC(max_iter=10000),param_grid =parameters,scoring='accuracy',cv=5,verbose =1)
# 模型在训练数据集上的拟合
grid_linear_svc.fit(X_train,y_train)
# 返回交叉验证后的最佳参数值
print(grid_linear_svc.best_params_, grid_linear_svc.best_score_)

out:
{'C': 1} 0.6967333333333333

# 模型在测试集上的预测
pred_ linear_svc = grid_linear_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test, pred_linear_svc)

经过5重交叉验证后，发现最佳的惩罚系数C为0.1，模型在训练数据集上
的平均准确率只有69.2%，同时，其在测试数据集的预测准确率也不足72%，说明线性可分SVM模型并不太适合该数据集的拟合和预测。接下来，使用非线性SVM模型对该数据集进行重新建模

# 使用网格搜索法，选择非线性SVM“类”中的最佳C值
kernel=['rbf','linear','poly','sigmoid']
C=[0.1,0.5,1,2,5]
parameters = {'kernel':kernel,'C':C}
grid_svc = model_selection.GridSearchCV(estimator = svm.SVC(max_iter=10000),param_grid =parameters,scoring='accuracy',cv=5,verbose =1)
# 模型在训练数据集上的拟合
grid_svc.fit(X_train,y_train)
# 返回交叉验证后的最佳参数值
print(grid_svc.best_params_, grid_svc.best_score_)

{'C': 5, 'kernel': 'rbf'} 0.9516666666666665

# 模型在测试集上的预测
pred_svc = grid_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test,pred_svc)

# 模型在测试集上的预测
pred_svc = grid_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test,pred_svc)
# 模型在测试集上的预测
pred_svc = grid_svc.predict(X_test)
# 模型的预测准确率
metrics.accuracy_score(y_test,pred_svc)
0.9596

经过5重交叉验证后，发现最佳的惩罚系数C为5，最佳的核函数为径向基
核函数。相比于线性可分SVM模型来说，基于核技术的SVM表现了极佳的效果，模型在训练数据集上的平均准确率高达97.34%，而且其在测试数据集的预测准确率也接近98%，说明利用非线性可分SVM模型拟合及预测手体字母数据集是非常理想的。

预测问题的解决

本节实战部分所使用的数据集来源于UCI网站，是一个关于森林火灾方面的预测，该数据集一共包含517条火灾记录和13个变量，其中变量area为因变量，表示火灾产生的森林毁坏面积，其余变量主要包含火灾发生的坐标位置、时间、各项火险天气指标、气温、湿度、风力等信息。接下来利用SVM模型对该数据集的因变量做预测分析：

# 读取外部数据
forestfires = pd.read_csv(r'forestfires.csv')
# 数据前5行
forestfires.head()

	X	Y	month	day	FFMC	DMC	DC	ISI	temp	RH	wind	rain	area
0	7	5	mar	fri	86.2	26.2	94.3	5.1	8.2	51	6.7	0.0	0.0
1	7	4	oct	tue	90.6	35.4	669.1	6.7	18.0	33	0.9	0.0	0.0
2	7	4	oct	sat	90.6	43.7	686.9	6.7	14.6	33	1.3	0.0	0.0
3	8	6	mar	fri	91.7	33.3	77.5	9.0	8.3	97	4.0	0.2	0.0
4	8	6	mar	sun	89.3	51.3	102.2	9.6	11.4	99	1.8	0.0	0.0

火灾发生的时间（month和day）为字符型的变量，如果将这样的变量带入模
型中，就必须对其做数值化转换。考虑到月份可能是火灾发生的一个因素，故将该变量做保留处理，而将day变量删除

# 删除day变量
forestfires.drop('day',axis = 1, inplace = True)
# 将月份作数值化处理
forestfires.month = pd.factorize(forestfires.month)[0]
# 预览数据前5行
forestfires.head()

	X	Y	month	FFMC	DMC	DC	ISI	temp	RH	wind	rain	area
0	7	5	0	86.2	26.2	94.3	5.1	8.2	51	6.7	0.0	0.0
1	7	4	1	90.6	35.4	669.1	6.7	18.0	33	0.9	0.0	0.0
2	7	4	1	90.6	43.7	686.9	6.7	14.6	33	1.3	0.0	0.0
3	8	6	0	91.7	33.3	77.5	9.0	8.3	97	4.0	0.2	0.0
4	8	6	0	89.3	51.3	102.2	9.6	11.4	99	1.8	0.0	0.0

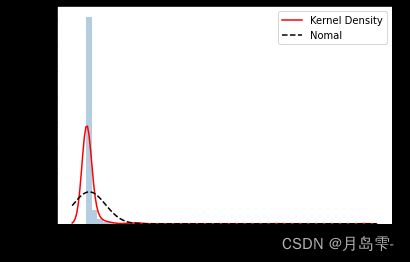
表中的应变量为area，是一个数值型变量，通常都需要对连续型的因变量做分布的探索性分析，如果数据呈现严重的偏态，而不做任何的修正时，直接带入到模型将会产生很差的效果。不妨这里使用直方图直观感受area变量的分布形态

# 导入第三方模块
import seaborn as sns
import matplotlib.pyplot as plt
from scipy.stats import norm
# 绘制森林烧毁面积的直方图
sns.distplot(forestfires.area, bins = 50, kde = True, fit = norm, hist_kws = {'color':'steelblue'}, 
             kde_kws = {'color':'red', 'label':'Kernel Density'}, 
             fit_kws = {'color':'black','label':'Nomal', 'linestyle':'--'})
# 显示图例
plt.legend()
# 显示图形
plt.show()

从分布来看，数据呈现严重的右偏。建模时不能够直接使用该变量，一般
都会将数据做对数处理

# 导入第三方模块
from sklearn import preprocessing
import numpy as np
from sklearn import neighbors
# 对area变量作对数变换
y = np.log1p(forestfires.area)
# 将X变量作标准化处理
predictors = forestfires.columns[:-1]
X = preprocessing.scale(forestfires[predictors])

在建模时必须对参数C、ε和y做调优处理，因为默认的SVM模型参数并不一定是最好的

# 将数据拆分为训练集和测试集
X_train,X_test,y_train,y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234)

# 构建默认参数的SVM回归模型
svr = svm.SVR()
# 模型在训练数据集上的拟合
svr.fit(X_train,y_train)
# 模型在测试上的预测
pred_svr = svr.predict(X_test)
# 计算模型的MSE
metrics.mean_squared_error(y_test,pred_svr)

out：
1.9268192310372871

# 使用网格搜索法，选择SVM回归中的最佳C值、epsilon值和gamma值
epsilon = np.arange(0.1,1.5,0.2)
C= np.arange(100,1000,200)
gamma = np.arange(0.001,0.01,0.002)
parameters = {'epsilon':epsilon,'C':C,'gamma':gamma}
grid_svr = model_selection.GridSearchCV(estimator = svm.SVR(max_iter=10000),param_grid =parameters,
                                        scoring='neg_mean_squared_error',cv=5,verbose =1, n_jobs=2)
# 模型在训练数据集上的拟合
grid_svr.fit(X_train,y_train)
# 返回交叉验证后的最佳参数值
print(grid_svr.best_params_, grid_svr.best_score_)


out：
Fitting 5 folds for each of 175 candidates, totalling 875 fits
{'C': 300, 'epsilon': 1.1000000000000003, 'gamma': 0.001} -1.9946668196316413

# 模型在测试集上的预测
pred_grid_svr = grid_svr.predict(X_test)
# 计算模型在测试集上的MSE值
metrics.mean_squared_error(y_test,pred_grid_svr)

out：
1.7455012238826288

经过5重交叉验证后，非线性SVM回归的最佳惩罚系数C为300、最佳的ε值
为1.1、最佳的Y值为0.001，而且模型在训练数据集上的负MSE值为-1.994。为了实现模型之间拟合效果的对比，构建了一个不做任何参数调整的SVM回归模型，并计算得到该模型在测试数据集上的MSE值为1.926，相比于经过调参之后的模型来说，这个值要高于1.746。进而可以说明，在利用SVM模型解决分类或预测问题时，需要对模型的参数做必要的优化。