Logistic回归-分类模型和梯度下降算法
Logistic回归
1. Logistc回归模型
回归:用一条直线对给定数据进行拟合(最佳拟合直线)
Logistic 回归:根据现有数据对分类边界建立回归方程,以此直线进行分类
给定数据集 \( [(x_{1},y_{1}),(x_{2},y_{2}),…,(x_{m},y_{m})] \) ,每个样本 x 有 d 个属性 \( x=[x_{1},x_{2},…,x_{d}] \) 。
对于给定数据集,该数据集的线性拟合公式为:
f ( x ) = w 0 x 0 + w 1 x 1 + w 2 x 2 + . . . + w d x d f(x) = w_{0}x_{0}+w_{1}x_{1}+w_{2}x_{2}+...+w_{d}x_{d} f(x)=w0x0+w1x1+w2x2+...+wdxd
f ( x ) = w T x f(x) = w^{T}x f(x)=wTx
其中 \( w^{T}=[w_{0},w_{1},w_{2},…,w_{d}] \)
若要进行分类任务(以二分类为例),需要找到一个单调可微的函数将分类任务的真实标记 y 和线性回归模型的预测值关联起来。
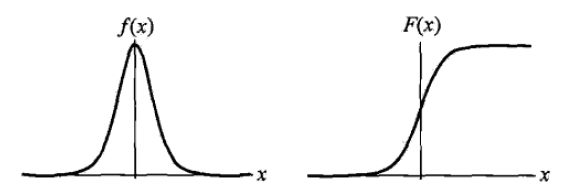
分类输出标记 y = {0 , 1} , 回归模型的预测值 \( z = w^{T}x \) , 因此需要一个函数将 z 转化为 0 / 1 值。 最理想的函数是 “ 单位阶跃函数 ”,但是这个函数是不连续的函数,它的跳跃点从0到1的跳跃过程很难处理。需要一个近似单位阶跃的函数,更容易处理且单调可微,这就是 “ 对几率函数(logistic function) ” 函数 ,它是“Sigmoid函数”的一种 。
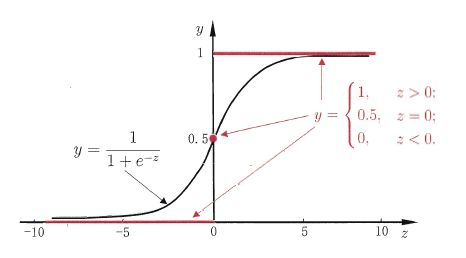
y w ( x ) = 1 1 + z − 1 = 1 1 + ( w T x ) − 1 y_{w}(x) = \frac{1}{1+z^{-1} }= \frac{1}{1+(w^{T}x)^{-1}} yw(x)=1+z−11=1+(wTx)−11
y = { 1 if z > 0 0.5 if z = 0 0 if z < 0 y = \begin{cases} 1 & \text{ if } z>0 \\ 0.5 & \text{ if } z=0 \\ 0 & \text{ if } z<0 \end{cases} y=⎩⎪⎨⎪⎧10.50 if z>0 if z=0 if z<0
y = 1 1 + e − ( w T x + b ) y = \frac{1}{ 1 + e^{-(w^{T}x+b)} } y=1+e−(wTx+b)1
l n y 1 − y = w T x + b ln\frac{y}{1-y}=w^{T}x+b ln1−yy=wTx+b
将上式中y作为样本为正例的可能性,1-y表示样本为负例的可能性,两者的比值 y/1-y 称为“几率”(odds),表示样本是正例的相对可能性,对“几率”取对数得到 ln(y/1-y) 称为“对数几率”(log odds/logit)。由此可见Logistic回归实际是在用线性回归模型的预测结果去逼近真实标记的对数几率。
我们将 ln(y/1-y)中的y视为类后验概率 P( y = 1 | x )于是将 对几率函数重写为
l n p ( y = 1 ∣ x ) p ( y = 0 ∣ x ) = w T x + b ln\frac{p(y=1|x)}{p(y=0|x)}=w^{T}x+b lnp(y=0∣x)p(y=1∣x)=wTx+b
在Logistic回归中,输出y=1的对数几率是输入x的线性函数,于是得到二项Logistic回归模型的条件概率:
p ( y = 1 ∣ x ) = e w T + b 1 + e w T + b p(y=1|x)=\frac{e^{w^{T}+b}}{1+e^{w^{T}+b}} p(y=1∣x)=1+ewT+bewT+b
p ( y = 0 ∣ x ) = 1 1 + e w T + b p(y=0|x)=\frac{1}{1+e^{w^{T}+b}} p(y=0∣x)=1+ewT+b1
对于任意给定的样本x,按照上两是计算得到 p(y=1|x) 和 P(y=0|x),比较两个条件概率的大小,将x分到概率较大的那一类。
考虑对样本进行分类的线性函数 \( w^{T}+b \),它的值域为实数域,通过Logistic回归条件概率将线性函数转化成概率,线性函数的值越接近正无穷,概率值就越接近1;线性函数值越接近负无穷,概率值就越接近0,这就是对几率函数的性质,这样的模型就是Logistic回归。
Logistic Regression虽然名字是回归,但它是一种分类学习算法,它的优点是分类时直接对分类可能性直接建模,无需事先假设数据分布,避免了假设分布不准确带来的问题;它不是仅预测出类别,而是类别的近似概率预测,这对很多需要概率辅助的分类任务很有用;对率函数是任意可导的凸函数,有很好的的数学性质,现有的很多数值优化算法都可直接用于求解最优解。
2. 模型参数估计
确定了分类器的函数形式,最终的问题就是如何确定最佳回归参数,向量 w 就是回归参数 ,使用极大似然估计来估计参数模型 w 和 b。
给定数据集 \( [(x_{1},y_{1}),(x_{2},y_{2}),…,(x_{m},y_{m})] \),将权值向量和特征向量扩充,仍记为w,x。
w = ( w 1 , w 2 , . . . , w d , b ) w = (w^{1},w^{2},...,w^{d},b) w=(w1,w2,...,wd,b)
x = ( x 1 , x 2 , . . . , x d , 1 ) x = (x^{1},x^{2},...,x^{d},1) x=(x1,x2,...,xd,1)
设 : \( p_{1}(x;w)=p(y=1|x;w) \), \( p_{0}(x;w)=p(y=0|x;w) \)
似然函数为:
∏ i = 0 m p ( x i ; w ) y i [ 1 − p ( x i ; w ) ] 1 − y i \prod_{i=0}^{m}p(x_{i};w)^{y_{i}}[1-p(x_{i};w)]^{1-y_{i}} i=0∏mp(xi;w)yi[1−p(xi;w)]1−yi
对数似然函数为:
L n ( w ) = ∑ i = 0 m [ y i l o g ( p ( x i ; w ) ) + ( 1 − y i ) l o g ( 1 − p ( x i ; w ) ) ] = ∑ i = 0 m [ y i l o g ( p ( x i ; w ) 1 − p ( x i ; w ) ) + l o g ( 1 − p ( x i ; w ) ) ] = ∑ i = 0 m [ y i ( w T x ) − l o g ( 1 + e w T x ) ] Ln(w) = \sum_{i=0}^{m}[y_{i}log(p(x_{i};w))+(1-y_{i})log(1-p(x_{i};w))]=\sum_{i=0}^{m}[y_{i}log(\frac{p(x_{i};w)}{1-p(x_{i};w)})+log(1-p(x_{i};w))]=\sum_{i=0}^{m}[y_{i}(w^{T}x)-log(1+e^{w^{T}x})] Ln(w)=i=0∑m[yilog(p(xi;w))+(1−yi)log(1−p(xi;w))]=i=0∑m[yilog(1−p(xi;w)p(xi;w))+log(1−p(xi;w))]=i=0∑m[yi(wTx)−log(1+ewTx)]
对Ln(w)求极大值,可以得到w的估计值。问题变成了对似然函数的最优化问题,Logistic回归常用的方法是梯度下降法和拟牛顿法。
3. 误差评估
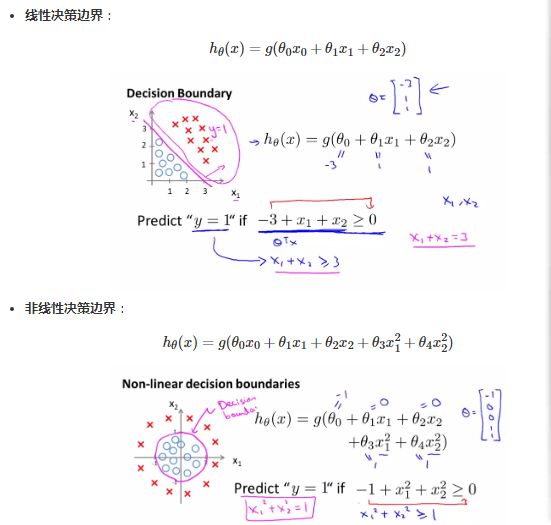
在logistic回归中明确了分类预测函数,其中\( z = w^{T}x \)是分类边界,即决策边界就是划分样本类别的边界,可以是点,可以是线,可以是面,"决策边界是预测分类函数的 \( y_{w}(x) \)的属性,不是训练集的属性,因为能够划分类别界限的是\( y_{w}(x) \),而训练集是用来训练调节参数"
在前面确定了 logistic regression的分类原理和方法,接下来要要评估分类效果,即评估\( y_{i} \) 和 \( f(x_{i}) \) 之间的误差,通过均方误差来描述误差,误差评估的函数又称为代价函数,均方误差是回归任务中常用的度量标准:
J ( w ) = 1 2 m ∑ i = 1 m ( f ( x i ) − y i ) 2 J(w)=\frac{1}{2m}\sum_{i=1}^{m}(f(x_{i})-y_{i})^{2} J(w)=2m1i=1∑m(f(xi)−yi)2
我们的目标就是通过调节参数 w 使 J(w)能够达到最小,
4. 优化算法-梯度下降法Gradient Descent
训练学习的目标就是不断调节参数w来使J(w)达到最小,通常使用梯度下降方法来调节w:
w j = w j − α ∂ ∂ w J ( w ) w_{j}=w_{j}-\alpha \frac{\partial }{\partial w}J(w) wj=wj−α∂w∂J(w)
梯度方向是函数值下降最为剧烈的方向。那么,沿着 J(w) 的梯度方向走,我们就能接近其最小值,或者极小值,从而接近更高的预测精度。学习率 α 是个相当玄乎的参数,其标识了沿梯度方向行进的速率,步子大了,很可能这一步就迈过了最小值。而步子小了,又会减缓我们找到最小值的速率。在实际编程中,学习率可以以 3 倍,10 倍这样进行取值尝试:α=0.001,0.003,0.01…0.3,1
4.1 批量梯度下降法(Batch Gradient Descent)
对一个大小为m的训练集,w的迭代过程如下,重复迭代直到收敛:
w j = w j + α 1 m ∑ i = 1 m ( y i − f ( x i ) ) x j i w_{j}=w_{j}+\alpha \frac{1}{m}\sum_{i=1}^{m}(y_{i}-f(x_{i}))x_{j}^{i} wj=wj+αm1i=1∑m(yi−f(xi))xji
矩阵表示如下:
w j = w j + α 1 m ( y − f ( x ) ) T x j w_{j}=w_{j}+\alpha \frac{1}{m}(y-f(x))^{T}x_{j} wj=wj+αm1(y−f(x))Txj
这种方法是批量梯度下降法,每次更新一次系数就要完整遍历一次数据集,如果训练集体积巨大,那么计算的复杂度太高。
4.2 随机梯度下降法(Stochastic Gradient Descent)
由于批量梯度下降法计算开销太大,一种改进方法是一次仅用一个样本点来更新回归系数,该方法称为随机梯度下降算法。由于可以在新样本到来时对分类器进行增量式更新,因而随机梯度下降算法是一个在线学习算法。与“在线学习”相对应,一次处理所有数据被称作是“批处理”。
重复迭代直至收敛:for i = 1 to m
w j = w j + α 1 m ( y i − f ( x i ) ) x j i w_{j}=w_{j}+\alpha \frac{1}{m}(y_{i}-f(x_{i}))x_{j}^{i} wj=wj+αm1(yi−f(xi))xji