78、Points2NeRF: Generating Neural Radiance Fields from 3D point cloud
简介
github:https://github.com/gmum/points2nerf
由于点云的大小和复杂性,处理这些点云具有挑战性,现有的方法通过将网格拟合到点云并渲染来解决这个问题,这种方法导致结果可视化的保真度降低,并遗漏了在计算机图形应用中至关重要的对象的颜色信息
论文利用超网络范式,训练模型使用相关颜色值获取3D点云,并返回从输入的2D图像重建3D对象的NeRF网络的权重,提供了有效的3D对象表示,并提供了一些优于现有方法的优点,包括调节nerf的能力和改进的泛化超出训练中看到的对象

采用具有相关颜色值的 3D 点云,并返回 NeRF 网络的权重,该网络以高保真度和连贯着色重建 3D 对象。
贡献点:
- 提出了一种名为Points2NeRF的新方法,该方法将超网络框架适应于NeRF架构,从而允许从3D点云生成辐射场
- 支持条件化nerf,这反过来又允许将模型推广到训练中看到的3D对象之外。
- 提供了一个生成模型,可以以连续的方式将3D对象表示为NeRF参数,从而实现对象空间内的插值。
实现流程
在Points2NeRF超网络是一种用于3D点云的自动编码器类型架构。构建一个自动编码器,它将输入3D点云并生成目标网络的权重- NeRF
超网络被定义为为解决特定任务的独立目标网络生成权重的神经模型,通过设计具有更少参数的超网络来减少可训练参数的数量
X = { X i } i = 1 , . . . , n = { ( x i , y i , z i , r i , g i , b i ) } i = 1 , . . . , n X = \{X_i\}_{i=1,...,n} = \{(x_i, y_i, z_i, r_i, g_i, b_i)\}_{i=1,...,n} X={Xi}i=1,...,n={(xi,yi,zi,ri,gi,bi)}i=1,...,n 是包含颜色点云的给定数据集,前三个元素编码位置,后三个编码RGB颜色。
自编码器的基本目标是通过一个典型的,但不一定是低维潜在空间 Z ⊆ R D Z⊆R^D Z⊆RD传输数据,同时最小化重构误差。寻找一个编码器 E : X → Z E: X→Z E:X→Z 和解码器 D : Z → X D: Z→X D:Z→X 函数,最小化了 X i X_i Xi 与其重建 D ( ε X i ) D(\varepsilon X_i) D(εXi)之间的重建误差。为此,使用一个基于PointNet架构的排列不变编码器和一个改进的解码器来产生权重而不是 row points,对于点云表示,关键的一步是定义合适的重构损失,可以在自动编码框架中使用。这里,使用了NeRF体渲染函数
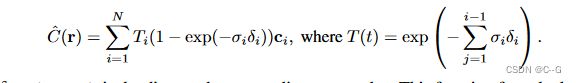

NeRF的架构相对简单,但使用了很多权重。因此,Hypernetwork必须生成许多参数。因此使用分块机制。在实践中,通过想要生成的层的索引来调节超网络来生成单个层的权重
Points2NeRF
Points2NeRF由三部分组成:hypernetwork, autoencoder and NeRF
将3D对象的参数化为函数 F Θ : R 5 → R 4 F_Θ: R^5→R^4 FΘ:R5→R4,给出位置(x, y, z)和观看方向(θ, ψ),返回颜色 c = (r, g, b)和体积密度 σ,不生成3D对象,而是想生成许多神经网络(每个对象都有不同的神经网络)来建模
使用超网络 H Φ : R 3 ⊃ X → Θ H_Φ: R^3⊃X→Θ HΦ:R3⊃X→Θ,对于点云 X ⊂ R 3 X \subset R^3 X⊂R3,它将权重 Θ 返回到对应的目标网络(NeRF) F Θ F_Θ FΘ
![]()
取一个输入点云 X ⊂ R 6 X\subset R^6 X⊂R6 (前三个元素编码位置,后三个编码RGB颜色),并将其传递给 H Φ H_Φ HΦ。因此,超网络将权重Θ 返回到目标网络 F Θ F_Θ FΘ。接下来,将2D图像集与目标网络 F Θ F_Θ FΘ生成的渲染图进行比较.
作为一个超网络,使用一个基于PointNet架构的置换不变编码器和一个改进的解码器来产生权重而不是原始点。
H Φ H_Φ HΦ 的架构包括:编码器(E)是一个类似PointNet的网络,将数据传输到低维潜在空间 Z ∈ R D Z∈R^D Z∈RD;解码器(D)(全连接网络),将潜在空间传输到目标网络的权重向量
超网络 H Φ ( X ) H_Φ(X) HΦ(X) 表示的自编码器结构 D ( ε X ) D(\varepsilon X) D(εX)
Mesh representation
利用体积密度 σ,得到体素表示。可以从网格(x, y, z)中预测点的内/外类别,然后可以通过等面提取方法(如Marching Cubes)渲染对象。当有网格表示时,可以预测所有顶点的颜色。通过在网格的顶点中使用颜色,可以为图形的面添加颜色

Generative model
基于自动编码器的生成模型是一种经典的自动编码器模型,其代价函数经过了修改,强制模型具有生成性,即确保传输到潜在空间的数据来自先验分布(典型的高斯分布)。因此,为了构建生成式自动编码器模型,将其代价函数添加到测量给定样本与先验分布的距离。
变分自动编码器(VAE)是能够通过应用变分推理来学习近似数据分布的生成模型。确保传输到潜伏空间Z的数据按标准法向密度分布。将与标准多元正态密度的距离相加。通过将Kullback-Leibler散度添加到成本函数中来获得生成模型,将其冷却为生成Point2nerf。


Voxel representation
NeRF网络是超网络的输出,它可以描述三维空间中给定点的占用情况。利用移动立方体算法可以对给定的点云进行网格重构。
为了将重建网格与原始网格进行比较,使用倒角距离(Chamfer Distance)定义为两个点 P 1 P_1 P1 和 P 2 P_2 P2 云之间的距离,这样:
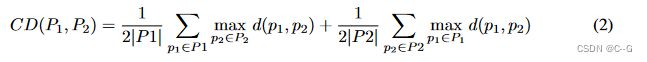
此外,在两个点云之间使用 F-Score 度量,其中一些阈值 t 定义为:

对于F-Score和倒角距离的计算,从原始网格和重建网格中随机采样3000点,使用阈值 t = 0.01来寻找F-Score的匹配点。
Limitations
Points2NeRF的主要限制是构建和存储NeRF架构所需的计算成本。在实际应用中,超网络必须产生大量的输出权值,因此训练时间占用了大量的时间。