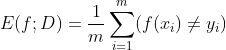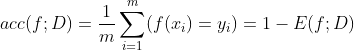吃瓜教程——DATAWHALE3月组队学习Task01
写在前面的话:
本系列文章旨在对本人21年3月参加机器学习组队学习所学到的的知识以及心得体会进行记录,文章知识性内容皆总结于周志华老师所著的《机器学习》("西瓜书")以及datawhale出版的教辅书"PUMPKIN BOOK"("南瓜书")。
本人为计算机专业大三在读,对机器学习、深度学习等人工智能相关领域兴趣颇深的小白一枚,所以在准备考研初期拿出一部分时间对机器学习进行初步的了解,为以后的学习或工作打基础,很荣幸能和队里的大佬们一起进步。
Task01:概览西瓜书+南瓜书第1、2章
由于前面两章公式类的知识较少,且一些美容现在理解起来较为困难,所以根据学习建议,在本篇文章中我只对一些概念性的基本知识和术语进行总结。
第一章:绪论
基本术语
(色泽 = 青绿; 根蒂 = 蜷缩; 敲声 = 浊响)
这里每对括号内是一条记录,"="的意思是"取值为"。
记录是关于对象或事件的描述,称为:"示例"(instance)或"样本"(sample);
数据集:一组记录的集合。
"色泽"、"根蒂"称为:属性(attribute)、特征(feature);
属性的取值: 属性值(attribute value);
属性张成的空间:样本空间(attribute space)、属性空间(sample space);
所以一个示例也可以称作:特征向量;
D = {x1,x2,...,xm}:包含m个示例的数据集;
xi = (xi1,xi2,...,xi3):用d个属性描述;组成d维的样本空间 ,d称为维数;
(色泽 = 青绿; 根蒂 = 蜷缩; 敲声 = 浊响, 好瓜)
"好瓜"称为标记(关于示例结果的信息);
拥有标记信息的示例称为:"样例"(example);
(xi, yi)表示第i个样例,yi是示例xi的标记;
所有标记的集合称为:标记空间(label space)、"输出空间";
学习任务:
预测离散值("好瓜"、"怀瓜")的学习任务称为:"分类"(classification);
对于只涉及两个类别的分类任务("二分类"(binary classification)),通常一个为正类一个为反类
预测连续值("瓜的成熟度:0.97")的学习任务:"回归"(regression);
预测任务希望通过对训练集进行学习,来建立一个从输入空间到输出空间的映射;
学习任务分类:
根据训练数据是否有标记信息分为:
监督学习(supervised learning)
无监督学习(unsupervised learning)
第二章:模型评估与选择
2.1经验误差与过拟合
错误率:样本分类错误数量在总样本中占的比率
![]()
精度:"1 - 错误率",通常用百分比形式
![]()
误差(error):学习器的实际预测输出与样本的真实输出之间的差异;
"在很多情况下,我们可以学得一个经验误差很小、在训练集上表现很好的学习器,例如甚至对所有训练样本都分类正确,即分类错误率为零,分类精度为100%,但这是不是我们想的的学习器呢?遗憾的是,这样的学习器在多数情况下都不好。"
训练误差(training error):在训练集上的误差;
泛化误差(generalization error):在新样本上的误差;
过拟合(overfitting):将训练样本自身的特点当作一般性质;
欠拟合(underfitting):训练样本的一半性质尚未学好;
2.2模型评估
测试集(testing test):测试学习器对新样本的判别能力,以新样本上的测试误差作为泛化误差的近似;
留出法(hold-out)
将数据集D划分为两个互斥的集合,训练集S和测试集T。即![]() ,
, ![]() ;
;
分层采样(stratified sampling):例如通过对 D进行分层采样而获得含 70% 样本的训练集S和含30% 样本的测试集T,若D包含500个正例、500 个反例,则分层采样得到S应包含350个正例、350个反例,而工则包含150个正例和 150 个反例;若S、T中样本类别比例差别很大,则误差估计将由于训练/测试数据分布的差异而产生偏差。
需要注意的问题:单次使用留出法得到的估计结果往往不够可靠,一般采用若干次随机划分、重复进行试验评估后取平均值作为评估结果。
常见做法:将2/3~4/5的样本用于训练,剩余的样本进行测试;
交叉验证法(cross validation)
将数据集 DD划分为k个大小相似的互斥子集。每次用k-1个子集的并作为训练集,剩下的1个作为测试集。通过k次训练和测试,返回k个测试结果的均值。
特例——留一法:假定数据集D中包含m个样本,令k=m。 优点:评估结果往往被认为比较准确;缺点:数据及较大时计算开销较大
自助法(boostrapping)
对数据集D,每次随机挑选一个样本将其放入D'中,再放回去,使其下一次采样时仍有可能被采到,整个过程重复m次(有放回随机采样)。
样本在m次采样中始终不被采集到的概率(求极限)
优点:在数据集较小,难以有效划分训练/测试集时很有用;此外,自助法能从初识数据集中产生多个不同的训练集;
缺点:会引入偏差;
因此,在数据量足够时,留出法和交叉验证法更常用。
调参与最终模型(parameter tuning)
现实中的做法是:对每个参数选定一个范围和变化步长;
验证集(validation set):模型评估与选择中用于评估测试的数据;
2.3 性能度量
性能度量(performance measure):反映了任务需求,模型的好坏不但取决于算法和数据,还决定于任务需求。
均方误差(mean squared error):回归任务最常用的性能度量;
错误率与精度
错误率
精度
查准率、查全率与F1
查准率P,查全率R分别定义为
![]()
其中TP为真正例,FP为假正例,NP为假反例,此外还有TN为真反例;
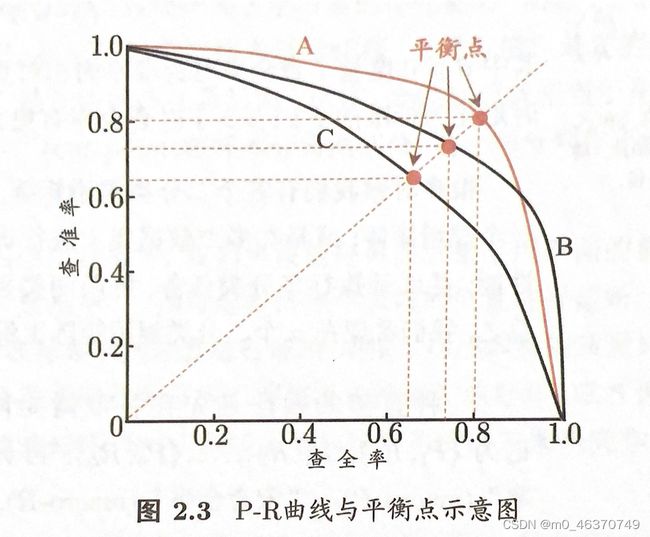
P-R曲线(图源 周志华 《机器学习》p31 图2.3)
若一个学习器的P-R曲线被另一个学习器的曲线完全包住,则可以断言后者的性能高于前者;
平衡点(BEP ,Break-Even Point)
查全率 = 查准率时的取值;
F1 度量
BEP还是过于简化了些,最常用的是F1度量;(total表示样例总数)