Datawhale组队学习之西瓜书task1

前言

本篇内容 Datawhale 2023年1月吃瓜教程组队学习 task1 的学习打卡，很开心能参加 Datawhale 的组队学习，希望这个寒假可以收获满满！

2.3.3 ROC与AUC及之后的内容看的不是很懂，先不放在笔记里了，等后续学完了回来补上！

数学符号问题

我发现周老师在西瓜书中并没有对一些数学符号做出说明，尤其是对我这种数学小白来说，有些符号都不知道该怎么查（汗颜），所以我查阅了一些资料，将常用数学符号列在最前面，方便后续查看。

写着写着突然发现一件很坑的事情，纸质版的书有符号表，手上电子版的书没有…不管了，不改了，就这样，反正大差不差（哭）

数字

• $x$：标量
• $\mathbf{x}$：向量
• $\mathbf{X}$：矩阵
• $\mathsf{X}$：张量
• $\mathbf{I}$：单位矩阵
• $x_i$, $[\mathbf{x}{]}_i$：向量$\mathbf{x}$第$i$个元素
• $x_{ij}$, $[\mathbf{X}{]}_{ij}$：矩阵$\mathbf{X}$第$i$行第$j$列的元素

集合论

• $\mathcal{X}$：集合
• $\mathbb{Z}$：整数集合
• $\mathbb{R}$：实数集合
• ${\mathbb{R}}^n$：$n$维实数向量集合
• ${\mathbb{R}}^{a\times b}$：包含$a$行和$b$列的实数矩阵集合
• $\mathcal{A}\cup \mathcal{B}$：集合$\mathcal{A}$和$\mathcal{B}$的并集
• $\mathcal{A}\cap \mathcal{B}$：集合$\mathcal{A}$和$\mathcal{B}$的交集
• $\mathcal{A}\setminus \mathcal{B}$：集合$\mathcal{A}$与集合$\mathcal{B}$相减，$\mathcal{B}$关于$\mathcal{A}$的相对补集

函数和运算符

• $f(\cdot )$：函数
• $\log (\cdot )$：自然对数
• $\exp (\cdot )$：指数函数
• $\mathbb{I}(\cdot )$：指示函数
• ${(\cdot )}^{\top }$：向量或矩阵的转置
• ${\mathbf{X}}^{-1}$：矩阵的逆
• $\odot$：按元素相乘
• $[\cdot ,\cdot ]$：连结
• $|\mathcal{X}|$：集合的基数
• $\Vert \cdot {\Vert }_p$：$L_p$ 正则
• $\Vert \cdot \Vert$：$L_2$正则
• $⟨\mathbf{x},\mathbf{y}⟩$：向量$\mathbf{x}$和$\mathbf{y}$的点积
• $\sum$：连加
• $\prod$：连乘
• $\stackrel{\mathrm{def}}{=}$：定义

微积分

• $\frac{dy}{dx}$：$y$关于$x$的导数
• $\frac{\partial y}{\partial x}$：$y$关于$x$的偏导数
• ${\nabla }_{\mathbf{x}}y$：$y$关于$x$的梯度
• ${\int }_a^{b}f(x)dx$：$f$在$a$到$b$区间上关于$x$的定积分
• $\int f(x)dx$：$f$关于$x$的不定积分

概率与信息论

• $P(\cdot )$：概率分布
• $z\sim P$：随机变量$z$具有概率分布$P$
• $P(X\mid Y)$：$X\mid Y$的条件概率
• $p(x)$：概率密度函数
• $E_x[f(x)]$：函数$f$对$x$的数学期望
• $X\perp Y$：随机变量$X$和$Y$是独立的
• $X\perp Y\mid Z$：随机变量$X$和$Y$在给定随机变量$Z$的条件下是独立的
• $\mathrm{Var}(X)$：随机变量$X$的方差
• ${\sigma }_X$：随机变量$X$的标准差
• $\mathrm{Cov}(X,Y)$：随机变量$X$和$Y$的协方差
• $\rho (X,Y)$：随机变量$X$和$Y$的相关性
• $H(X)$：随机变量$X$的熵
• $D_{\mathrm{KL}}(P\Vert Q)$：$P$和$Q$的KL-散度

---

第一章

1.1 一些纯概念

数据集（data set）：关于某个事件 / 对象的数据（记录）的集合

示例（instance）/ 样本（sample）：数据集中的一条记录

属性（attribute）/ 特征（feature）：反映事件或对象在某方面的表现或性质

属性值（attribute value）：属性的取值

属性空间（attribute space）/ 样本空间（sample space）/ 输入空间（input space）：属性张成的空间

特征向量（feature vector）：属性空间中的一个点，即一个样本

维数（dimensionality）：一个样本的属性数量

训练（training）：从数据中学得模型的过程

训练数据（training data）：训练中使用的数据

训练样本（training sample）：训练数据中的样本

训练集（training set）：训练样本组成的集合

假设（hypothesis）：模型学得的数据中某种潜在规律

学习器（learner）：即模型

标记（label）：关于样本结果的信息

样例（example）：拥有标记的样本

标记空间（label space）/ 输出空间（output space）：所有标记的集合

分类（classification）：预测离散值的学习任务

回归（regression）：预测连续值的学习任务

测试（testing）：使用模型进行预测的过程

测试样本（testing sample）：被预测的样本

聚类（clustering）：将训练集分为一些组，同组之内含有潜在的联系

簇（cluster）：聚类所形成的组，每组都称为一个簇

监督学习（supervised learning）：训练数据具有标记信息

无监督学习（unsupervised learning）：训练数据不具有标记信息

泛化（generalization）/ 归纳（induction）：从具体的事实归结出一般性规律，泛化能力尤其指模型适用于新样本的能力

特化（specialization）/ 演绎（deduction）：从基础原理推演出具体情况

归纳学习（inductive learning）：广义上指从样例中学习，狭义上指从训练数据中学得概念

概念学习（concept learning）：狭义的归纳学习

1.2 假设空间&版本空间

首先给出一个比较抽象的例子：

编号	属性1	属性2	属性3	好？
1	A	a	1	好
2	B	b	2	坏
3	A	c	1	好

假设空间（hypothesis space）是所有假设的集合，以表格中的数据来说，属性1有两种可能，属性2有三种可能，属性3有两种可能，再考虑到属性存在任意取值都合适的情况（用通配符 * 表示）和不存在“好”这一假设（用$\varnothing$表示），那么假设空间的大小便为 3*4*3+1=37

在假设空间中搜索的过程中，不断删除与正例不一致的假设和与反例一致的假设，得到了所谓的版本空间（version space），即与训练集一致的“假设集合”

以上述表格举例，由编号1可以得到（A, a, 1）,（*, a, 1）,（A, *, 1）,（A, a, *）,（*, *, 1）,（*, a, *）,（A, *, *）,（*, *, *）这些假设成立，再由编号3得到（A, c, 1）,（*, c, 1）,（A, *, 1）,（A, c, *）,（*, *, 1）,（*, c, *）,（A, *, *）,（*, *, *）假设成立，取两者交集，得（A, *, 1）,（*, *, 1）,（A, *, *）,（*, *, *）成立，由编号2得（*, *, *）不成立，因此此例的版本空间为（A, *, 1）,（*, *, 1）,（A, *, *）

不难看出，一般数据越多，能完全拟合数据的假设就越少，因此版本空间越小

1.3 归纳偏好

任何一个模型都需要也一定具有归纳偏好（inductive bias），即偏好某一种数据分布或者问题，否则将无法产生确定的结果。

根据“没有免费的午餐”定理（NFL定理），无论两个学习算法是怎样实现的，它们的期望性能相同，数学表达式如下：
$$\sum _f{E}_{ote}({\mathfrak{L}}_a|X,f)=\sum _f{E}_{ote}({\mathfrak{L}}_b|X,f)=2^{|\mathcal{X}|-1}\sum _{\mathbf{x}\in \mathcal{X}-X}P(\mathbf{x})\cdot 1$$
但是要指出的是，我们在训练一个模型时，并不是想让它同时能完成所有的任务，我们只需要让它完成某一种或者某一类任务即可。

因此NFL定理的意义就是：脱离具体问题谈算法优劣毫无意义，我们要做的就是让算法的偏好与我们想解决的问题更加相配。

---

第二章：

2.1 新概念

误差（error）：模型的实际输出与样本真实输出的差异

错误率（error rate）：$E=a/m$，指m个样本中有a个分类错误（在分类问题中）

精度（accuracy）：即正确率，精度=1-错误率

训练误差（training error）/ 经验误差（empirical error）：模型在训练集上的误差

泛化误差（generalization error）：模型在新样本上的误差

过拟合（overfitting）：训练误差小，泛化误差大，即模型学习了过多训练数据的特殊特性

欠拟合（underfitting）：训练误差和泛化误差都大，即模型还没学会训练数据的一般特性

2.2 测试集的选择

首先，测试集（testing set）是从原有数据集中划分出来，用来测试模型的集合，目的是用测试误差（testing error）来近似泛化误差。

选取测试集的原则是不能出现在训练集中。（不能让模型做过一模一样的试卷

下面介绍三种方法从数据集$D$中产生训练集$S$与测试集$T$

2.2.1 留出法

留出法（hold-out）将数据集分成了两个互斥的集合，一个作为$S$，另一个作为$T$。

使用留出法应该注意两点：

1. 划分数据集时要尽可能保证数据的分布一致性。举个极端的例子，测试集中全为正例，那这显然是没有意义的。
2. 每次划分的结果不同，最后的模型也会有一些差异，因此最好多次使用留出法取平均值

最后，从划分数量上来说，一般划分出2/3~4/5给训练集，其余数据给测试集

2.2.2 交叉验证法

交叉验证法（cross validation），又称k折交叉验证（k-fold cross validation），将数据集分成了k个互斥集合，每次选取k-1个子集的并集作为训练集，剩下的一个子集作为测试集，重复k次。

当然，划分成k个子集时也需要考虑分布的一致性，更常见的，可以采取不同的划分来多次进行交叉验证，比如“10次10折交叉验证”，就是用十种不同的划分将原来的数据集划分成十个集合，总计进行了10*10=100次训练与测试。

2.2.3 自助法

对于数据量充足的情况，留出法和交叉验证法更加常用，但对于数据量较小的场合，则可以使用自助法（bootstrapping）

自助法：对于一个含有m个样本的数据集$D$，每次随机从$D$中复制一个样本到$D^{\prime }$中，重复m次，用$D^{\prime }$作为训练集，$D\setminus D^{\prime }$作为测试集

样本在m次采样中始终不被采到的概率是$(1-\frac{1}{m}{)}^m$，绘制函数图像如下，可以看出当m>3时，不被采到的概率就来到了30%，因此使用自助法，最终会有30%+的数据不出现在训练集中（对m取极限可知函数极限为36.8%）

2.3 性能度量

衡量模型泛化能力的评价标准，即为性能度量（performance measure）

2.3.1 如何度量回归任务

回归任务最常用的度量方式是使用均方误差（mean squared error, MSE）：
$$E(f;D)=\frac{1}{m}\sum _{i=1}^m(f({\mathbf{x}}_i)-y_i{)}^2$$
其中数据集$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),...,({\mathbf{x}}_m,y_m)\}$，$y_i$是${\mathbf{x}}_i$的真实标记，$f({\mathbf{x}}_i)$是模型对${\mathbf{x}}_i$的预测结果

2.3.2 如何度量分类任务

错误率与精度

本章开头已经用通俗的语言介绍过了错误率$E$与精度$acc$，这里给出数学定义：
$$\begin{array}{rl}E(f;D)& =\frac{1}{m}\sum _{i=1}^m\mathbb{I}(f({\mathbf{x}}_i)\ne y_i{)}^2\\ acc(f;D)& =\frac{1}{m}\sum _{i=1}^m\mathbb{I}(f({\mathbf{x}}_i)=y_i{)}^2\\ & =1-E(f;D)\end{array}$$

查准率、查全率、F1

考虑分类时的所有结果，可以绘制出下表：

查准率$P$（precision）与查全率$R$（recall）的定义为：
$$\begin{array}{r}P=\frac{TP}{TP+FP}\\ R=\frac{TP}{TP+FN}\end{array}$$
从现实意义上来说，查准率$P$体现预测出的好结果有多少是正确的，查全率$R$体现真正好的结果中有多少被预测出来了

为了直观体现查准率、查全率与模型的关系，可以绘制P-R图：

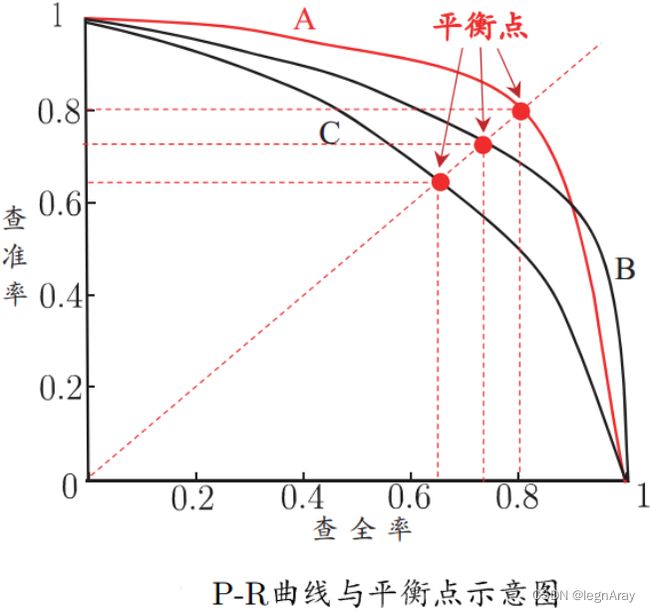
从图上可以看出，查准率与查全率是一对比较矛盾的度量，一者升高另一者就会下降。

当某个模型对应的P-R曲线完全包住另一模型时，可以认为该模型优于另一模型（比如上图的A与C），但如果曲线有相交，就不太好判断了，这时常用$F1$度量：
$$F1=\frac{2\times P\times R}{P+R}=\frac{2\times TP}{m+TP-TN}$$
因为有时人们对查准率与查全率的偏好不同，这时就常用$F_{\beta }$度量，当$\beta >1$时查全率影响更大，当$0<\beta <1$时查准率影响更大，$\beta =1$时即为$F1$度量：
$$F_{\beta }=\frac{(1+{\beta }^2)\times P\times R}{{\beta }^2\times P+R}$$