OBB的计算python实现

OBB的经典生成算法：使用PCA（主成分分析）。
主成分分析有一个关键的线性代数计算步骤，即求解协方差矩阵的特征值和特征向量，这一点必须使用数值分析算法而不能用解题用的基本行变换手段，因为现代程序最大的特点就是干一些枯燥重复的事情——迭代.

在这里主要介绍三维的思路，黑盒模型：

obb的参数（中心点、三轴向量、三轴半长，以确定一个空间中的矩形）= f（点集）

1. 实现步骤

步骤① 分解点集的xyz分量

即把所有点的 x、y、z 值分别放到独立的数组中

步骤② 对x、y、z这三个随机变量（一维数组）求协方差矩阵

步骤③ 对步骤②中的协方差矩阵求解特征值与特征向量，特征向量构造列向量矩阵M

步骤④ 将点集的几何中心平移至坐标系原点，并全部乘以M矩阵进行旋转变换

步骤⑤ 将旋转变换后的点的坐标，求xMax、xMin、yMax、yMin、zMax、zMin，进而求出obb中心坐标、obb半长

步骤⑥ 将obb中心坐标左乘M的逆，得到此中心坐标在原来坐标系的坐标值

步骤⑦ 将步骤⑥中得到的原坐标系下的obb中心坐标平移回原处（平移向量与步骤④的平移向量刚好是相反向量）

最后，得到：

特征向量作为obb的三个轴朝向
obb的三个方向的半长
obb的中心坐标
其中，计算难点在于步骤③，最经典的做法是使用 Jacobi 迭代计算算法，在数值分析课程中是一节基础，Jacobi 算法还是可以优化的。
还可以使用矩阵分解算法等进行优化。

参考：简述OBB算法：使用PCA计算

2. 代码实现OBB

2.1. OOBB in 2D

是之前讨论过的关于 bounding box，如果使用 AABB 也许不是最紧密的 bounding box，更紧密的有时候也叫 OBB oriented bounding-box 或者 OOBB Object Oriented Bounding Boxes，所以建议可以使用 PCA 来计算。

根据文章OBB generation via Principal Component Analysis，首先有一些例子点：

(3.7, 1.7), (4.1, 3.8), (4.7, 2.9), (5.2, 2.8), (6.0, 4.0), (6.3, 3.6), (9.7, 6.3), (10.0, 4.9), (11.0, 3.6), (12.5, 6.4)

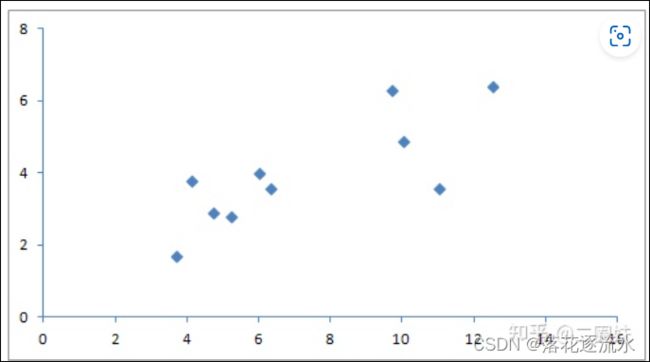
然后它算 covarience matrix 是：

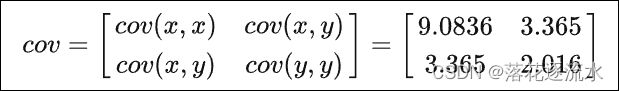
用 numpy 来处理：

points = np.asarray(  [ (3.7, 1.7), (4.1, 3.8), (4.7, 2.9), (5.2, 2.8), (6.0, 4.0), (6.3, 3.6), (9.7, 6.3), (10.0, 4.9), (11.0, 3.6), (12.5, 6.4) ] )
np.cov( points )
// 上面这个不对，形状都完全不对，然后看了一下，好像应该这么写：

>>> np.cov( points, rowvar = False )
array([[10.09288889,  3.73888889],
       [ 3.73888889,  2.24      ]])

这下形状对了，但是结果还是不一样啊，这个时候机智的我想到了在计算方差等等等老是出现的一个问题，那就是到底除以 N 还是除以 N-1，所以我来试验一下:

np.cov( points, rowvar = False ) / 10 * 9
array([[9.0836, 3.365 ],
       [3.365 , 2.016 ]])

cool! 跟上面的 covarience matrix 一致了， 下一步来计算 covarience matrix 的 eigenvector。Hmmm，既然是计算 eigenvector，那么乘以一个常数是没有影响的，继续使用 numpy:

>>> np.linalg.eig( np.cov( points, rowvar = False ))
(array([11.58827588,  0.74461301]), array([[ 0.92849112, -0.37135459],
       [ 0.37135459,  0.92849112]]))

出了一堆结果，根据这篇NumPy: Eigenvalues & Eigenvectors:

来解读，所以知道 eigenvector 是：

yep，又跟文章对上了， 根据文章，现在要继续的是

Projecting onto these vectors allow us to determine the OBB’s center and half-extent lengths, giving us the following image
文章就直接给出了结果，

然后突然发现了这里： Create the Oriented Bounding-box (OBB) with Python and NumPy

原来上面的除以 N 还是除以 N-1 是可以用 bias = 1 这个参数来描述的，完整的代码此处有：cool！

import matplotlib.pyplot as plt
import numpy as np

a  = np.array([(3.7, 1.7), (4.1, 3.8), (4.7, 2.9), (5.2, 2.8), (6.0,4.0), (6.3, 3.6), (9.7, 6.3), (10.0, 4.9), (11.0, 3.6), (12.5, 6.4)])
ca = np.cov(a,y = None,rowvar = 0,bias = 1)

v, vect = np.linalg.eig(ca)
tvect = np.transpose(vect)



fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111)
ax.scatter(a[:,0],a[:,1])

#use the inverse of the eigenvectors as a rotation matrix and
#rotate the points so they align with the x and y axes
ar = np.dot(a,np.linalg.inv(tvect))

# get the minimum and maximum x and y 
mina = np.min(ar,axis=0)
maxa = np.max(ar,axis=0)
diff = (maxa - mina)*0.5

# the center is just half way between the min and max xy
center = mina + diff

#get the 4 corners by subtracting and adding half the bounding boxes height and width to the center
corners = np.array([center+[-diff[0],-diff[1]],center+[diff[0],-diff[1]],center+[diff[0],diff[1]],center+[-diff[0],diff[1]],center+[-diff[0],-diff[1]]])

#use the the eigenvectors as a rotation matrix and
#rotate the corners and the centerback
corners = np.dot(corners,tvect)
center = np.dot(center,tvect)

ax.scatter([center[0]],[center[1]])    
ax.plot(corners[:,0],corners[:,1],'-')

plt.axis('equal')
plt.show()

关键在下面的这几行代码：

tvect = np.transpose(vect)
ar = np.dot(a,np.linalg.inv(tvect))
mina = np.min(ar,axis=0)
maxa = np.max(ar,axis=0)
diff = (maxa - mina)*0.5
corners = np.array([center+[-diff[0],-diff[1]],center+[diff[0],-diff[1]],center+[diff[0],diff[1]],center+[-diff[0],diff[1]],center+[-diff[0],-diff[1]]])
corners = np.dot(corners,tvect)
center = np.dot(center,tvect)

其实上面的 transpose inverse， 变换 corner， 再变换回来，是不是可以这样理解，这一整个其实在做的就是坐标变换。我们由上图的 xy坐标变换到了 PCA 的轴的方向，然后再变换回来，我们才能得到正确的 center 和 corner.

2.2. OBB in 3D

看见以上的代码，我想直接代入3D points感觉应该也是 ok 的，唯一需要注意的是 3D 的 corners 维度更多，上面的代码基本上可以直接套用到 3D 的情况，令我惊讶的是我用 bunny 看到的结果居然是这样

我好惊讶，然后我看到 Fitting Oriented Bounding Boxes 这篇里的例子跟我一样，当用 points 来 fit OBB 的话就会这样

参考：Fitting Oriented Bounding Boxes
参考：Bounding Box - OOBB
参考：Create the Oriented Bounding-box (OBB) with Python and NumPy
参考：OBB generation via Principal Component Analysis

3. 函数实现

# 应用于2D、3D
def PCA(points):
    pointArray = np.array(points)
    ca = np.cov(pointArray,y = None,rowvar = 0,bias = 1)
    v, vect = np.linalg.eig(ca)
    tvect = np.transpose(vect)
    #use the inverse of the eigenvectors as a rotation matrix and
    #rotate the points so they align with the x and y axes
    ar = np.dot(pointArray,np.linalg.inv(tvect))
    
    # get the minimum and maximum x and y 
    mina = np.min(ar,axis=0)
    maxa = np.max(ar,axis=0)
    diff = (maxa - mina)*0.5
    # the center is just half way between the min and max xy
    center = mina + diff
    
    #get the 8 corners by subtracting and adding half the bounding boxes height and width to the center
    pointShape = pointArray.shape
    if pointShape[1] == 2:
        corners = np.array([center+[-diff[0],-diff[1]],
                        center+[diff[0],-diff[1]],
                        center+[diff[0],diff[1]],
                        center+[-diff[0],diff[1]],
                        center+[-diff[0],-diff[1]]])
    if pointShape[1] == 3:
        #get the 8 corners by subtracting and adding half the bounding boxes height and width to the center
        corners = np.array([center+[-diff[0],-diff[1],-diff[2]],
                    center+[diff[0],-diff[1],-diff[2]],                    
                    center+[diff[0],diff[1],-diff[2]],
                    center+[-diff[0],diff[1],-diff[2]],
                    center+[-diff[0],diff[1],diff[2]],
                    center+[diff[0],diff[1],diff[2]],                    
                    center+[diff[0],-diff[1],diff[2]],
                    center+[-diff[0],-diff[1],diff[2]],
                    center+[-diff[0],-diff[1],-diff[2]]])   
    
    #use the the eigenvectors as a rotation matrix and
    #rotate the corners and the centerback
    corners = np.dot(corners,tvect)
    center = np.dot(center,tvect)
    radius = diff
    if pointShape[1] == 2:
        array0,array1 = np.abs(vect[0,:]),np.abs(vect[1,:])
        index0,index1 = np.argmax(array0),np.argmax(array1)
        radius[index0],radius[index1] = diff[0],diff[1]
    if pointShape[1] == 3:
        array0,array1,array2 = np.abs(vect[0,:]),np.abs(vect[1,:]),np.abs(vect[2,:])
        index0,index1,index2 = np.argmax(array0),np.argmax(array1),np.argmax(array2)
        radius[index0],radius[index1],radius[index2] = diff[0],diff[1],diff[2]
    eigenvalue = v
    eigenvector = vect
    return corners, center, radius,eigenvalue,eigenvector

调用测试

corners, pcaCenter, pcaRadius,eigenvalue,eigenvector = PCA(rasPts)
print("corners", corners)
print("center", center)
print("radius", radius)
print("eigenvalue", eigenvalue)
print("eigenvector", eigenvector)

输出

corners [[-214.08716255 -287.34124873  329.15531199]
 [-206.02520693 -222.36772698  349.92398594]
 [-155.32541073 -228.84508711  350.5074316 ]
 [-163.38736634 -293.81860887  329.73875765]
 [-165.25498872 -305.17224576  365.98288493]
 [-157.1930331  -240.19872401  386.75155889]
 [-207.8928293  -233.72136387  386.16811323]
 [-215.95478492 -298.69488563  365.39943928]
 [-214.08716255 -287.34124873  329.15531199]]
center [-185.64009782 -263.76998637  357.95343544]
radius [25.55761109 34.34345453 19.01334956]
eigenvalue [221.80978801 109.57123123  54.06473478]
eigenvector [[ 0.11737252  0.99187275 -0.04911345]
 [ 0.94593748 -0.12672077 -0.29857014]
 [ 0.30236728  0.01141432  0.95312315]]