Python 数据处理数据挖掘（六）：决策树模型 之 CART算法

声明：本文为学习笔记，侵权删

一、基尼系数&CART算法

CART（Classification And Regression Tree - 分类/回归树）是决策树算法的其中一种，依靠基尼系数进行分类。基尼系数描述的是：从一个系统中随机抽取两个样本，这两个样本不同类的概率。概率越大，基尼系数越大，反之基尼系数越小。基尼系数越小（即：几乎取不到不一样的，也就是说基本上都是一样的，那不同类的那个就容易被区分出来），系统的系统区分度越高（基尼系数越小），也就越适合做分类预测。决策树的目标就是缩小每个样本空间的基尼系数。

基尼系数公式：

T是样本空间

pi是该样本空间中每一个类所占总样本的比例

即：基尼指数是1减去各个类所占比例的平方和

如果有一个样本空间T，通过某种规则，分为了T1,T2两个子样本空间，这是gini(T)的公式：

p1,p2分别是T1，T2所占总样本空间T的比例。比如T1样本数=200，T2样本数=300，T样本数=500。则p1=0.4,p2=0.6

这个公式也可以推广到3,4个...多个子样本空间的情况。

CART算法描述：首先使用单个特征k和阈值(如：高度<2.5)将训练集分为两个子集。选中的k和也就是决策树的根节点。那怎么选出k和呢？当然是这么选能让某个成本函数最小啦~

CART的分类成本函数如下，本质上就是降低基尼系数（其实就是上面那个公式...）：

 代表左右子集的实例数，m就是父节点的总实例数。

 代表左右节点的基尼系数。

 根节点由此确立之后，按相同的逻辑，对子集进一步划分，直至达到最大深度，或找不到可以减小基尼系数的分割方式，递归停止。

注意一：CART算法是一种贪婪算法，从顶层开始搜索最优分裂，然后每层用相同的逻辑递归。但在这个过程中（比如递归到树的第三层的时候），算法并不会返回去看当前的解还有没有更优的划分方法（比如，根节点划分的阈值调一下，也许第二层的基尼系数会变大，但到第三层也许会比当前的好，CART并不会管这茬）。毫无疑问，当前解是一个不错的解，但CART不能保证这就是最优解。Unfortunately，寻找最优树是一个已知的NP完全问题，时间复杂度为O(exp(m))，强行要求最优解消耗太大，因此我们只能接受CART提供的不错的解。不过放心，这个解虽不一定是最好的，但一定是很值得信赖的。

注意二：CART算法默认使用基尼系数来衡量模型的，但也可以通过为超参数criterion赋值'entropy'，使用熵来衡量。熵越小，数据集中的实例越属于同一类。使用熵还是基尼系数并不会造成太大的差别，产生的树很相似。但基尼系数的计算速度更快，所以选为默认。基尼系数更倾向于从树枝中分裂出最常见的类型，而熵倾向于产生平衡的树。

参考：Hands-On Machine Learning  作者：Aurelien Geron

二、分类决策树

决策树分为分类决策树和回归决策树，这里更多讨论分类决策树。

同时要注意，这里的决策树使用的是CART算法。sklearn中的决策树模型都用的是CART算法。CART仅生成二叉树，非叶子节点只拥有两个子节点。当然也有非二叉树的模型，像J48这样的，但sklearn并不提供，因此这次不做讨论。

分类决策树树用来处理离散型数据，也就是数据种类有限的数据，它输出的是样本的类别。

回归树用来处理连续型数据，也就是数据在某段区间内的取值，输出是一个数值。

sklearn中的分裂决策树和回归决策树会自动尝试各种根节点的搭配组合，找到基尼系数最小的一种，并以此作为分类的依据。决策树分别计算数据属于每一类的概率，找到概率最大的一类，这个数据就会被分到这一类。

决策树有一个独特的性质，即它几乎不要求数据准备（注意是几乎，文末会提），完全不需要数据缩放，标准化，因此用决策树的时候数据预处理的过程简化了很多。

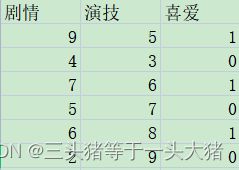
例如，这里有一部分用户对不同电影的喜爱程度，0是不喜欢，1是喜欢。评判标准为{剧情，演技}。显然，这里只有0,1两种情况，是离散的数据，因此想要判断用户是否喜欢电影，需要用的是分类决策树。

import pandas as pd
from sklearn.tree import DecisionTreeClassifier

data = pd.read_csv(r"D:\Python Code\dataMining\电影.csv",encoding="GBK")
#剧情与演技是自变量，喜爱与否是因变量
x=data[["剧情","演技"]]
y=data["喜爱"]
#生成一个深度为2的树
model = DecisionTreeClassifier(max_depth=2,random_state=1)
model.fit(x,y)
#预测4种电影是否受欢迎。每个列表中，前一项是剧情，后一项是演技
pre=model.predict([[8,6],[6,8],[6,7],[4,8]])
print(pre)

输出：
[1 1 1 0]

如果数据稍微复杂一些，也可以手动调整一下树的深度（这里还计算了模型预测的正确率）：

import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

data = pd.read_csv(r"D:\Python Code\dataMining\电影.csv",encoding="GBK")
#把数据集中年龄这一列的数据改为数值，便于处理
data["年龄"] = data["年龄"].replace({"轻":0,"中":1,"高":2})

x=data.drop(columns = "喜爱")
y=data["喜爱"]
#划分训练集与验证集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=1)
#生成一个深度为3的树
model = DecisionTreeClassifier(max_depth=3,random_state=1)
model.fit(x_train,y_train)

#求模型的正确率
y_pred = model.predict(x_test)
score = accuracy_score(y_pred,y_test,normalize=True)#normalize = True,返回正确分类的比例， false返回正确分类的样本数
print(score) #输出：1.0 评分满分，主要是因为我的数据集太小了，如果是大的数据集就基本上不会有这种情况了

前面提到，决策树分类其实是计算一个数据属于各个类的概率，找到最大概率的类。我们其实是可以看到每个数据属于每一类的概率的：

probability = model.predict_proba(x_test)
print(probability)
#print(probability[:,1])  一个小知识点：读取二维列表的某一列的完整数据, 这里读的是第二列

输出：
[[0. 1.]
 [1. 0.]]

输出的左列是分类为0（不喜欢），右列是分类为1（喜欢）。
这里的测试总共包含两组数据，第一组：0的概率为0, 1的概率为1。
还是数据集太小导致的，数据集大一点的话可能就是：0的概率是0.1,1的概率是0.9

三、模型参数的自动优化

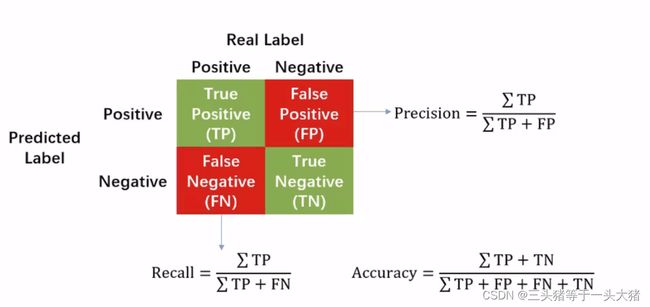
这里需要三个概念TPR,FPR,ROC,AUC，可以百度一下，挺好理解的哈~

一般在二分类问题中都会用到这些概念。

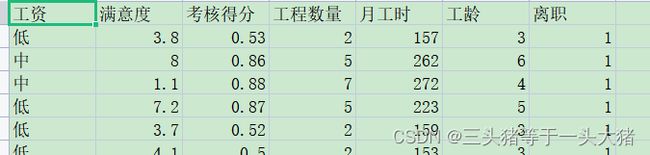
在本例中，离职为positive，未离职为negative。为了更好得演示，这里换一组更复杂的数据集：

 计算tpr,fpr。（其余部分和上面的例子一样）

#计算tpr,fpr,thres 其中thres是threshol的意思，是一个阈值，概率大于该阈值的时候才能分类为positive
fpr,tpr,thres = roc_curve(y_test,probability[:,1]) #因为本例中取离职（1）为positive
print(fpr)
print(tpr)
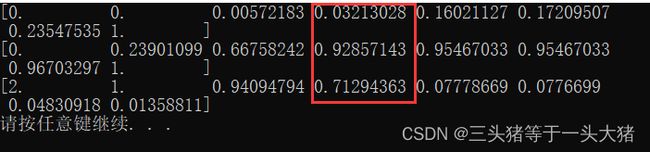
print(thres)

输出：

这个输出是啥意思呢？以红色框框里的数据为例：最下面的0.7129...是阈值，即：预测离职的概率大于0.7129的时候被判为离职，此时fpr=0.032,tpr=0.928。根据得到的fpr,tpr就可以画出ROC曲线：

 简单来说，ROC曲线越陡峭，模型越好，或者说，ROC曲线下的面积越大，模型越好，但这只能定性分析，判定ROC曲线的优劣有专门的判定规则：AUC值（其实就是曲线下面积）

 AUC = 0.5~0.7 效果较差

AUC = 0.7~0.85 效果较好

AUC = 0.85~1 效果很好

#计算AUC
from sklearn.metrics import roc_auc_score
AUC = roc_auc_score(y_test,probability[:,1])
print(AUC) #0.9684401481001393

3.1 K折交叉验证

关于K折交叉验证的概念，可以看这里。

注意：若数据集较小，可以适当提高K值，保证每次迭代有足够的数据用于训练。若数据集较大，可适当减小K值，减小程序运行成本。

#计算K折交叉验证
#scoring="roc_auc"代表以ROC曲线的AUC值作为评分标准
#cv=5 代表这是5折交叉验证（默认为3折交叉验证）
#得到的结果是长度为5的列表
AUC_score = cross_val_score(model,x_train,y_train,scoring="roc_auc",cv=5)
print(AUC_score) 输出[0.95820899 0.9693086  0.961101   0.96984419 0.9672071 ]
print(AUC_score.mean()) 输出0.9651339760890151

通过K折交叉验证得到的检验结果比前面只用一次AUC值更为准确。同时，K折交叉验证也常与Gridsearch网格搜索配合使用。

3.2 Gridsearch网格搜索

网格搜索是啥呢？是一个以K折交叉验证为底层逻辑的选择最佳参数的枚举机制。用大白话说，就是告诉机器我要选出哪些参数，且在什么范围里选。然后机器就一个个带进去试，同时会给机器提供一个判定的标准（比如标准是最高的AUC的值），从而找到最佳的参数。

举个例子就是：

x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.2,random_state=1)
#Gridsearch
model = DecisionTreeClassifier()
#需要选择的参数要通过字典格式输入Gridsearch
try_param = {"max_depth":[1,2,3,4,5,6,7,8,9]}
from sklearn.model_selection import GridSearchCV
#scoring 确定选择的标准
grid_search = GridSearchCV(model,try_param,scoring="roc_auc",cv=5)
grid_search.fit(x_train,y_train)
best_param = grid_search.best_params_
print(best_param)

输出：{'max_depth': 7}

这里想要知道最大深度为几的树分类效果最好，评价标准是auc, 然后创建一个Gridsearch的模型，让他自己跑就行了。最终就会得到最好的那个值。但Gridsearch有个缺陷就是：只能求出有限范围内的最佳值，比如，万一max_depth=11时候效果比7的时候要好，通过这个方法并不能得到max_depth=11。

当然，这里输出max_depth=7效果最好，那么就可以用max_depth=7建立分类决策树，然后接下来的步骤就很常规了。此外，还可以尝试调整更多的超参数，像min_samples_split(分裂前节点必须有的最小样本数)，min_samples_leaf（与前一个类似，但表现为加权实例总数的占比）、max_leaf_nodes（最大叶子节点的数量）、max_features（分裂每个节点评估的最大特征数量）。

最后，因为决策树模型喜欢正交的决策边界，即决策边界都垂直与坐标轴（不出现斜线），因此如果对数据集旋转一下，可能会导致模型变得很复杂。想象一下，原本两类数据可以用一条水平直线划分，但我把这个数据集的数据旋转45度，因为决策边界不为斜线，那决策树在旋转后的数据集熵训练出来的决策边界会由多条竖线和横线构成，像台阶那样。因此，还记得上面提到说决策树模型几乎不需要数据预处理吗？在数据集被旋转了之后，决策树依然可以搭建起合适的模型，但会变得复杂且泛化能力也许会变差。因此数据集可能在传入决策树训练之前，需要先进行PCA降维之类的操作。