自组织特征图（SOFM）详解
文章目录
- 1. SOM 简介
- 2. SOM 生物学基础
- 3. K-means
-
- 3.1 K-means 原理
- 3.2 聚类数量K的确定
- 3.3 随机初始化陷阱
- 4. SOM 图解
- 5. SOM 学习过程
- 6. SOM 应用
几种无监督学习算法及应用：
| 算法 | 应用 |
|---|---|
| Self-Organizing Map ，SOM | Feature Detection |
| Deep Boltzmann Machines | Recommendation Systems |
| AutoEncoders | Recommendation Systems |
1. SOM 简介
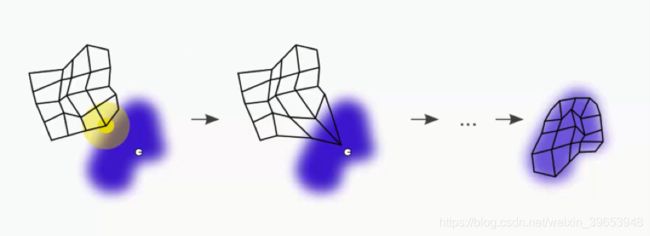
自组织映射（Self-Organizing Map ，SOM）或自组织特征映射（Self-Organizing Feature Map ，SOFM） 是一种类型的人工神经网络（ANN），其使用已训练的无监督学习以产生的一个低维（通常为二维），离散表示训练样本的输入空间（称为Map），因此是一种降维方法。下图示例显示了如何降低复杂数据集的维度。
自组织图不同于其他人工神经网络，因为它们应用竞争性学习而不是纠错学习（例如具有梯度下降的反向传播），并且从某种意义上说，它们使用邻域函数来保留输入空间的拓扑属性。
1980年，芬兰教授 T·Kohonen 提出一种自组织特征映射网 （ SOFM ）， 又称 Kohonen 网 。 Kohonen 认为 ，一个神经网络接受外界输入模式时， 将会分为不同的对应区域， 各区域对输入模式具有不同的响应特征，而且这个过程是自动完成的。 自组织特征映射正是根据这一看法提出来的 ，其特点与人脑的自组织特性相类似。
2. SOM 生物学基础
生物学研究表明，在人脑感觉通道上，神经元的组织原理是有序排列的，输入模式接近，对应的兴奋神经元也相近。大脑皮层中神经元这种相应特点不是先天形成的，而是后天的学习自组织形成的。
对于某一图形或某一频率的特定兴奋过程是自组织特征映射网中竞争机制的生物学基础。神经元的有序排列以及对外界信息的连续映像在自组织特征映射网中也有反映，当外界输入不同的样本时，网络中哪个位置的神经元兴奋在训练开始时时随机的。但自组织训练后会在竞争层形成神经元的有序排列，功能相近的神经元非常靠近，功能不同的神经元离的较远。这一特点与人脑神经元的组织原理十分相似。
3. K-means
K-means 是一个聚类算法，与SOM一样都属于无监督机器学习算法。下面以二维数据集为例介绍 K-means 的原理。
-
第一步：选择群集数。
在将数据集处理成类别之前，必须商定群集数。 -
第二步：随机选择 K 点作为质心。
需要选择一个随机 （x，y） 点。它不一定是数据集中的观察图之一， 任何 x - y 值都可以。最重要的是需要尽可能多的质心作为集群。 -
第三步：将每个数据点分配给离它最近的质心。
当数据点被分配给它们的质心时，这些中心周围会出现聚类。为了避免混淆，在本例中使用欧几里德距离。 -
第四步：计算并放置每个群集的新质心。
下面介绍。 -
第五步：将数据点重新分配给现在最接近它们的质心。
如果重新分配，则需要返回步骤 4 并重复，直到质心不再发生变化。如果没有，则意味着已经完成了该过程，模型训练停止，聚类完成。
3.1 K-means 原理
下面展示了该实例的可视化过程。
- 第一步：选取 K 值。
设置 K-means 的 cluster 数 K=2。有关 K 的选取有如下注意事项：
- K 值的选择大多数还是通过理解与洞察手动来选择；
- 可以通过 elbow method 来选择K值，但是它并不通用，因为很多情况下，肘部点并不明确；
- 大多数情况下，根据后续的目的来选择 K 值，看后续需求来决定；
- 第二步：随机选择 K 个聚类中心。
- 第三步：将每个数据点分配给离它最近的质心。
在两个质心之间画一条直线，然后在这条线中间画一条垂直线。
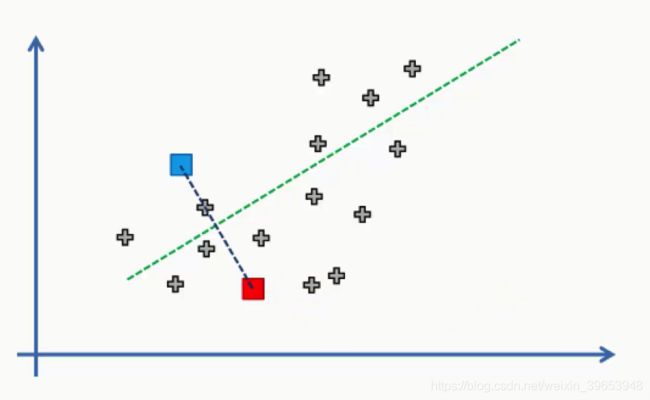
从上图中可以看到，落在绿线上方的任何数据点都更接近蓝色质心，而它下面的任何点更接近红色质心。然后，我们按数据点的质心颜色对数据点进行着色。
- 第四步：计算并放置每个集群的新质心（计算聚类内所有点的 x-y 坐标平均值）。
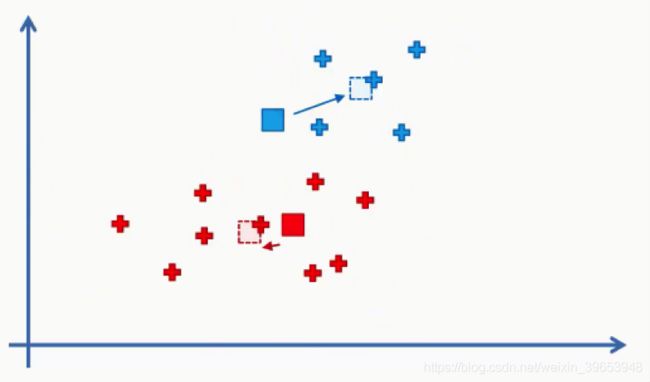
第五步：将数据点重新分配给现在离它们最近的质心，并重复步骤四和步骤五过程。
3.2 聚类数量K的确定
假设有如下数据分布，不同的K值对应不同的聚类结果。
聚类的目标是最小化 within-cluster sum of squares (WCSS)，其定义如下：
arg min S ∑ i = 1 k ∑ x ∈ S i ∥ x − μ i ∥ 2 = arg min S ∑ i = 1 k ∣ S i ∣ Var S i \underset{\mathbf{S}} {\operatorname{arg\,min}} \sum_{i=1}^{k} \sum_{\mathbf x \in S_i} \left\| \mathbf x - \boldsymbol\mu_i \right\|^2 = \underset{\mathbf{S}} {\operatorname{arg\,min}} \sum_{i=1}^k |S_i| \operatorname{Var} S_i Sargmini=1∑kx∈Si∑∥x−μi∥2=Sargmini=1∑k∣Si∣VarSi
这相当于最小化同一聚类中点的成对平方偏差：
arg min S ∑ i = 1 k 1 2 ∣ S i ∣ ∑ x , y ∈ S i ∥ x − y ∥ 2 \underset{\mathbf{S}} {\operatorname{arg\,min}} \sum_{i=1}^{k} \, \frac{1}{2 |S_i|} \, \sum_{\mathbf{x}, \mathbf{y} \in S_i} \left\| \mathbf{x} - \mathbf{y} \right\|^2 Sargmini=1∑k2∣Si∣1x,y∈Si∑∥x−y∥2
变量说明：
- x n x_n xn： d d d 维的 n n n 个观测值；
- k：聚类数量；
- S：聚类集合数量；
- μ i \mu_i μi：聚类集和 S i S_i Si 的均值；
上式进一步简化为：
∑ x ∈ S i ∥ x − μ i ∥ 2 = ∑ x ≠ y ∈ S i ( x − μ i ) ( μ i − y ) \sum_{\mathbf x \in S_i} \left\| \mathbf x - \boldsymbol\mu_i \right\|^2 =\sum_{\mathbf{x}\neq\mathbf{y} \in S_i}(\mathbf x - \boldsymbol\mu_i)(\boldsymbol\mu_i - \mathbf y) x∈Si∑∥x−μi∥2=x=y∈Si∑(x−μi)(μi−y)
上例中，三个聚类中心的WCSS计算为：
WCSS随聚类中心数量变化的关系图：
当聚类中心数量从 1 增加到 2 时，WCSS从8000减小到3000，从 2 增加到 3 时，WCSS 仍然大幅减少，从 3000 减小到 1000。但是，从该点开始，更改变得非常小，每个群集的 WCSS 仅下降 200 甚至更少。
elbow method 的意思是在此图上查找最后一个发生巨大变化且之后更改无关紧要的点。在这种情况下，在 3 个群集到达该点。
3.3 随机初始化陷阱
下面介绍 K-means 聚类算法中，聚类中心的选取。
两种不同的聚类中心选取结果。
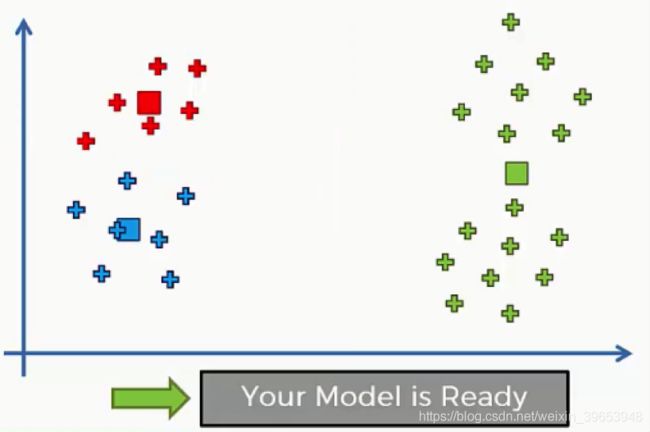
可以看出不同的聚类中心初始化，其聚类结果也不相同。无论使用 R 还是 Python，K-means 都是在后台实现的，只需要确保在创建 K-means 时使用正确的工具，它会自动处理这种情况。常用的算法为 K-means +。
4. SOM 图解
一个非常基本的自组织图。
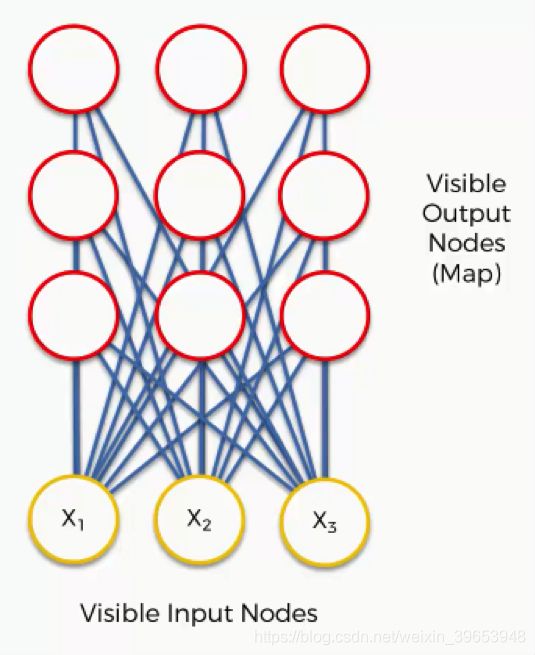
输入向量有三个输入节点，九个输出节点。SOM 旨在降低数据集的维度，三个输入节点表示数据集中的三个特征序列（维度），但每列可以包含数千行。SOM 中的输出节点始终为二维节点。
将上图转换为与传统的神经网络类似的结构如图所示。
它仍然是完全相同的网络，但节点的不同定位。它包含输入节点和输出节点之间的相同连接。SOM 与神经网络存在差异：
SOM中每个连接都分配了权重。
SOM中的权重与卷积神经网络中的权重不同。卷积神经网络中，将输入节点的值乘以权重，最后应用激活函数。而对于 SOM，没有激活函数。
权重与此处的节点不分离。在 SOM 中，权重属于输出节点本身。SOM 中的输出节点包含权重作为坐标，而不是添加权重的结果。
在此示例中为 3D 数据集，每个输入节点表示 x 坐标。SOM 将压缩到一个输出节点中，该节点具有三个权重。如果处理 20 维数据集，则在这种情况下，输出节点将有 20 个权重坐标。
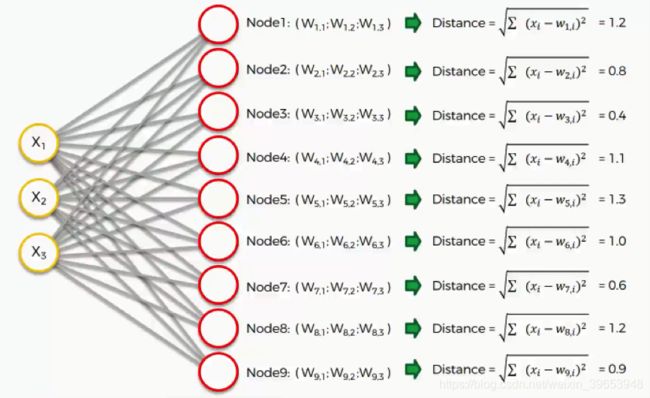
如图所示，节点 3 是最接近的，距离为 0.4。因此将此节点设置为最佳匹配单元（best-matching unit，BMU）。
假设有更大的数据集，某次求解出的BMU如图所示：
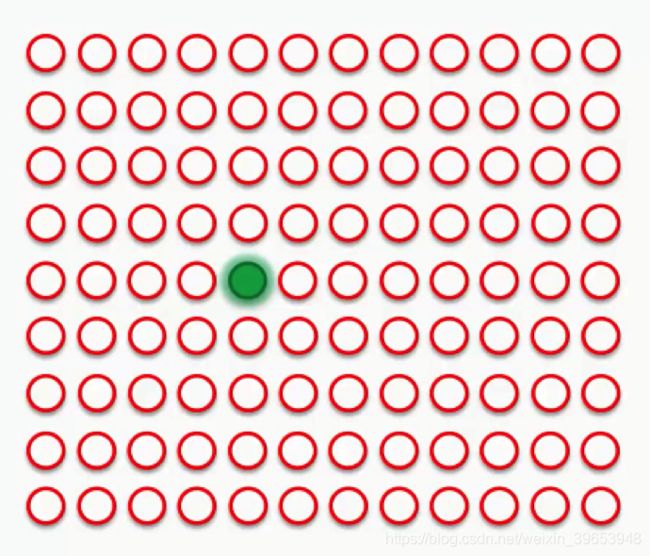
现在，新的 SOM 必须更新其权重，以便它更接近数据集的第一行。需要这样做的原因是，输入节点无法更新，而控制着输出节点。
简单地说，SOM 通过将 BMU 向数据点拉伸，越来越接近数据点。最终目标是让 Map 与数据集对齐。
BMU（黄色圆圈）最接近数据点（小白圆）。当我们将 BMU 拖近数据点时，附近的节点也会被拉近到该点。
下一步是在 BMU 周围绘制半径，任何属于该半径的节点都会更新其权重，以便将其拉近到匹配的数据点（行）。
节点离 BMU 越近，在其更新中要添加到的权重越大。
如果选择另一行匹配，将得到一个不同的 BMU。然后，使用新的 BMU 重复相同的过程。
有时，一个节点会落在两个半径上，一个在绿色BMU周围绘制，另一个在蓝色BMU周围绘制。 在这种情况下，该节点将受到其最近的BMU的影响更大，尽管它仍会受到较小程度的影响。
但是，如果该节点与两个BMU几乎等距，则其权重更新将来自两个的组合。
如果 Map 包含多个最佳匹配单位 （BBUS），而不是只有两个。
采取左上角的紫色节点。 已对其进行更新，以使其更接近与之匹配的行。 落入其半径的其他节点将进行相同的更新，以便与它们一起拖动。 其他BMU及其外围节点也是如此。
当然，在此过程中，外围节点要经历一些推拉操作，因为它们中的许多节点都落在一个以上BMU的半径之内。 这些BMU的联合力量会更新它们，最接近的BMU最具影响力。
随着重复此过程，每个BMU的半径都会缩小。 这是Kohonen算法的独特功能。 这意味着每个BMU将开始在更少的节点上施加压力。
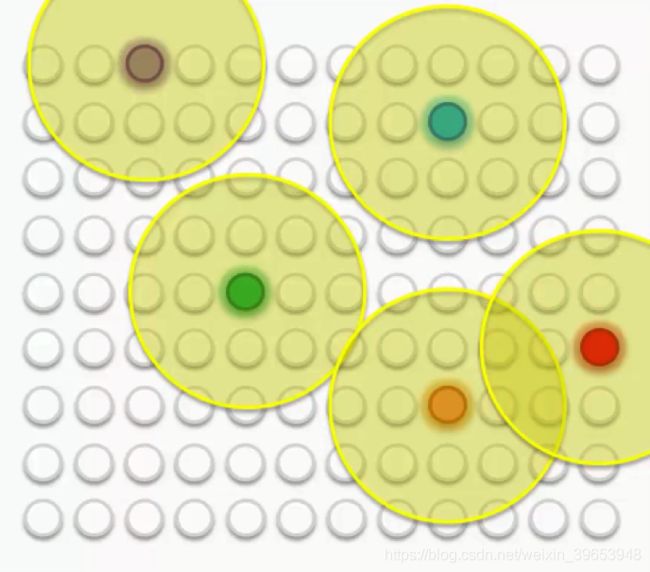
在继续进行过程中，从尝试仅让BMU接触数据点，转向尝试将整个地图与数据集更精确地对齐。
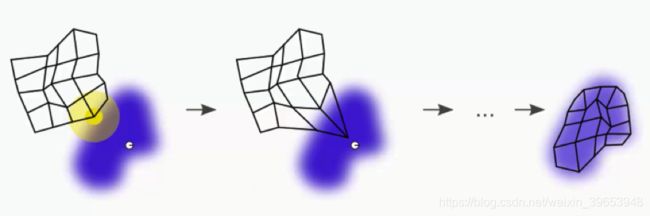
最终的 Map为：
在节点和不同 BMU 之间进行推送和拉取之后，每个节点都分配了一个 BMU。
5. SOM 学习过程
自组织地图的学习过程的第一步是初始化连接上的所有权重。之后，数据集中的随机样本用作网络的输入。然后，网络计算哪个神经元最像输入数据（输入向量）的权重。为此，使用以下公式：
D i s t a n c e 2 = ∑ i = 0 n ( i n p u t i − w e i g h t i ) 2 Distance^2 = \sum^n_{i=0} (input_i - weight_i)^2 Distance2=i=0∑n(inputi−weighti)2
其中 n n n 是连接数（权重）。具有最佳结果的映射神经元称为最佳匹配单元或 BMU。从本质上讲，这意味着输入向量可以用这个映射神经元表示。现在，自组织映射不仅在学习过程中计算这一点，还尝试使其与接收的输入数据"更近"。
这意味着此连接上的权重以计算距离更小的方式更新。不过，这并不是唯一能做到的事情。BMU 的邻域权重也会被修改，因此它们更接近此输入向量。这就是整个地图如何向这一点"拉"。为此，我们必须知道将更新的邻居的半径。此半径最初很大，但每次迭代（epoch）都会减少。因此，训练自组织地图的下一步实际上是计算提到的半径值。应用以下公式：
σ ( t ) = σ 0 e − t λ \sigma(t) = \sigma_0e^{- \frac{t}{\lambda}} σ(t)=σ0e−λt
其中 t t t 是当前迭代， σ 0 \sigma_0 σ0 是地图的半径。公式中的 λ \lambda λ 定义为：
λ = k / σ 0 \lambda = k/\sigma_0 λ=k/σ0
其中 k k k 是迭代次数。此公式利用指数衰减，使半径随着训练的进行而变小，这是最初的目标。简而言之，这意味着每次通过数据迭代都会使相关点更接近输入数据。自行组织地图用这种方式进行了微调。
当计算当前迭代的半径时，将更新半径内所有神经元的权重。神经元离 BMU 越近，其权重变化越大。这是通过使用此公式实现的：
W e i g h t ( t + 1 ) = W e i g h t ( t ) + θ ( t ) ⋅ L ( t ) ⋅ ( i n p u t ( t ) − W e i g h t ( t ) ) Weight(t + 1) = Weight(t) + \theta(t) \cdot L(t) \cdot (input(t) - Weight(t)) Weight(t+1)=Weight(t)+θ(t)⋅L(t)⋅(input(t)−Weight(t))
这是主要的学习公式， L ( t ) L(t) L(t) 表示学习率。与半径公式类似，它利用指数衰减，并且在每个迭代中越来越小：
L ( t ) = L 0 e − t λ L(t) = L_0e^{-\frac{t}{\lambda}} L(t)=L0e−λt
除此之外，我们提到，如果神经元更接近BMU，神经元的权重将更改变。在公式中，使用 θ ( t ) \theta(t) θ(t) 处理。此值的计算方式如下：
θ ( t ) = e − d i s t B M U / 2 σ ( t ) 2 \theta(t) = e^{-distBMU/2\sigma(t)^2} θ(t)=e−distBMU/2σ(t)2
显然，如果神经元更接近BMU，distBMU更小，并且 θ ( t ) \theta(t) θ(t) 值更接近1。这意味着这种神经元的权重值将改变更多。
整个过程会重复进行，SOM 学习过程中最重要的步骤：
- 权重初始化；
- 输入向量从数据集中选择，并用作网络的输入；
- 计算 BMU；
- 将计算更新的邻居的半径；
- 半径内神经元的每个权重都经过调整，使其更像输入向量；
- 对数据集的每个输入向量重复从 2 到 5 的步骤。
当然，在自组织地图的学习过程中，方程式有很多变化。事实上，已经做了很多研究，试图获得迭代次数、学习速率和邻域半径的最佳值。发明者特沃·科约宁建议，这个学习过程应该分为两个阶段。在第一阶段，学习率从0.9降低到0.1，邻域半径从晶格直径的一半降低到立即环绕的节点。
在第二阶段，学习率将进一步从0.1降低到0.0。但是，在第二阶段中会有双重或更多的迭代，邻域半径值应保持在 1，这意味着仅 BMU。这意味着第一阶段将用于学习，第二阶段将用于微调。
6. SOM 应用
自组织特征图是一个非常有趣的概念，与神经网络世界的其它部分非常不同。它使用无监督的学习为输入数据创建地图或掩码。它们为大型或难以解释的数据集提供了优雅的解决方案。由于这种高适应性，在许多领域应用，一般主要用于分类。最初，Kohonen使用它们进行语音识别，但今天它们也用于书目分类、图像浏览系统和图像分类、医学诊断、数据压缩等。
参考：
1.SOM简介：https://rubikscode.net/2018/08/20/introduction-to-self-organizing-maps/
2.SOM Python：https://rubikscode.net/2018/08/27/implementing-self-organizing-maps-with-python-and-tensorflow/
3.SOM简介：https://www.cnblogs.com/huty/p/8519246.html
4.SOM GitHub：https://github.com/alexarnimueller/som
5.SOM 系列介绍：https://www.superdatascience.com/blogs/self-organizing-maps-soms-plan-of-attack
6.SOM 介绍：http://www.ai-junkie.com/ann/som/som1.html
7.SOM词条：https://en.wikipedia.org/wiki/Self-organizing_map
8.如何选择K-means的cluster数：https://www.cnblogs.com/yan2015/p/5239970.html