nms、softnms、softernms
softnms:https://arxiv.org/abs/1704.04503 代码:http://bit.ly/2nJLNMu
softernms:https://arxiv.org/abs/1809.08545 代码:https://github.com/yihui-he/KL-Loss
1 NMS
目标检测的pipeline中,通过神经网络的处理,输出了一系列的预测框,为了保证检测的召回率,这些预测框一般都相互重叠(多个检测框对应同一个目标)。为了提升检测效果,一般会使用置信度过滤+NMS进行检测结果的后处理。
置信度过滤即人为设定置信度阈值,只保留超过阈值的检测框。
NMS用于消除同一目标上的多个重复框,一般是针对各类目标单独应用NMS,NMS的实现思路为:
- 设定两个数据集,B表示所有的预测框,D表示保留的检测框集合;
- 将置信度超过阈值的预测框按照置信度从高到底排序;
- 选取当前B中置信度最高的检测框M为基准,计算B中其余检测框和M之间的IOU,将B中和M的IOU大于阈值的检测框从B中移除,将M放入D中;
- 重复步骤3,直到B为空时停止迭代。最终,D中的检测框即为最终的检测结果。
NMS的计算复杂度为 O ( n 2 ) O(n^2) O(n2),n为起始阶段B中检测框的数量。
实现代码部分,摘抄自:https://blog.csdn.net/weixin_41665360/article/details/99818073
import numpy as np
def nms(dets, Nt):
x1 = dets[:,0]
y1 = dets[:,1]
x2 = dets[:,2]
y2 = dets[:,3]
scores = dets[:,4]
order = scores.argsort()[::-1]
#计算面积
areas = (x2 - x1 + 1)*(y2 - y1 + 1)
#保留最后需要保留的边框的索引
keep = []
while order.size > 0:
# order[0]是目前置信度最大的,肯定保留
i = order[0]
keep.append(i)
#计算窗口i与其他窗口的交叠的面积
xx1 = np.maximum(x1[i], x1[order[1:]])
yy1 = np.maximum(y1[i], y1[order[1:]])
xx2 = np.minimum(x2[i], x2[order[1:]])
yy2 = np.minimum(y2[i], y2[order[1:]])
#计算相交框的面积,不相交时用0代替
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
inter = w * h
#计算IOU:相交的面积/相并的面积
ovr = inter / (areas[i] + areas[order[1:]] - inter)
#inds为保留的检测框的索引
inds = np.where(ovr < thresh)[0]
#+1是为了跳过当前保留的检测框(索引0),因为计算重叠面积时的索引起点为1,x1[order[1:]]
order = order[inds + 1]
return keep
# test
if __name__ == "__main__":
dets = np.array([[30, 20, 230, 200, 1],
[50, 50, 260, 220, 0.9],
[210, 30, 420, 5, 0.8],
[430, 280, 460, 360, 0.7]])
thresh = 0.35
keep_dets = nms(dets, thresh)
print(keep_dets)
print(dets[keep_dets])
NMS简单有效,是目标检测的标准后处理过程。但在更高的目标检测需求下,也存在四方面的缺陷:
- 对于密集目标的场景,本身属于两个目标的检测框可能IOU很高,如果直接将置信度较大的那个检测框删除掉,有可能造成漏检,降低了模型的召回率。softnms就是基于解决这个问题进行设计的;
- 阈值难以确定,nms的阈值是一个人为设置的参数,设置的过高容易造成误检,设置的过低容易造成漏检,这个参数很难确定;
- nms将置信度得分作为预测准确度的衡量指标,但在一些情况下,置信度得分高的预测框不一定更加准确,softernms是为了解决这个问题进行设计的;
- nms的处理包含了较多的循环步骤,GPU并行化的实现难度较大,在预测框数量很多时,nms的处理耗时较多。
2 SoftNMS
softnms适合于解决密集检测场景下因nms过程中直接删除高度重叠目标而造成的目标漏检的问题。如下图所示场景:
 两匹马的检测框高度重叠,使用NMS时,在IOU阈值较低时,置信度更低的那匹马身上的检测框会被直接删除,造成漏检。
两匹马的检测框高度重叠,使用NMS时,在IOU阈值较低时,置信度更低的那匹马身上的检测框会被直接删除,造成漏检。
下面的式子中,M表示当前置信度最高的检测框, b i b_i bi表示某个候选检测框, N t N_t Nt表示nms的阈值。
nms的计算公式可以描述为:
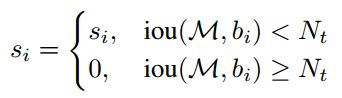
因此,作者提出的解决方案是,在nms过程中,对于和高置信度目标高IOU重叠的检测目标,不是直接删除而是降低其置信度得分,这样做使得这些目标在后面有机会被当作正确的检测框得以保留,这样就避免了目标的误检。
在设计目标得分降低策略时,一个指导原则是,一个检测框和高置信度检测框的IOU越大,其置信度的下降幅值应该越大。
所以作者首先提出了线性的置信度降低策略,即:
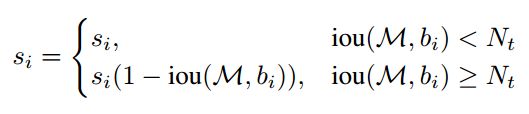
这样的策略的确达到了预想目的,但缺点是在 N t N_t Nt处函数不连续,会造成检测框的置信度跳变,对检测结果产生了较大的波动。
因此,作者又提出了连续版本的高斯置信度降低策略,即:

高斯版本的置信度下降策略,即为作者提出的soft nms。
softnms的计算复杂度和nms相同,都为 O ( n 2 ) O(n^2) O(n2),可以看作是nms的泛化,而nms也可以称作hard nms,是soft nms的二值化特例。
 代码摘抄自:https://blog.csdn.net/weixin_41665360/article/details/99818073
代码摘抄自:https://blog.csdn.net/weixin_41665360/article/details/99818073
def py_cpu_softnms(dets, Nt=0.3, sigma=0.5, thresh=0.5, method=2):
"""
py_cpu_softnms
:param dets: boexs 坐标矩阵 format [x1, y1, x2, y2, score]
:param Nt: iou 交叠阈值
:param sigma: 使用 gaussian 函数的方差
:param thresh: 最后的分数阈值
:param method: 使用的方法,1:线性惩罚;2:高斯惩罚;3:原始 NMS
:return: 留下的 boxes 的 index
"""
N = dets.shape[0]
# the order of boxes coordinate is [x1,y1,x2,y2]
x1 = dets[:, 0]
y1 = dets[:, 1]
x2 = dets[:, 2]
y2 = dets[:, 3]
areas = (x2 - x1 + 1) * (y2 - y1 + 1)
for i in range(N):
# intermediate parameters for later parameters exchange
tB = dets[i, :4]
ts = dets[i, 4]
ta = areas[i]
pos = i + 1
if i != N-1:
maxscore = np.max(dets[:, 4][pos:])
maxpos = np.argmax(dets[:, 4][pos:])
else:
maxscore = dets[:, 4][-1]
maxpos = -1
if ts < maxscore:
dets[i, :] = dets[maxpos + i + 1, :]
dets[maxpos + i + 1, :4] = tB
dets[:, 4][i] = dets[:, 4][maxpos + i + 1]
dets[:, 4][maxpos + i + 1] = ts
areas[i] = areas[maxpos + i + 1]
areas[maxpos + i + 1] = ta
# IoU calculate
xx1 = np.maximum(dets[i, 0], dets[pos:, 0])
yy1 = np.maximum(dets[i, 1], dets[pos:, 1])
xx2 = np.minimum(dets[i, 2], dets[pos:, 2])
yy2 = np.minimum(dets[i, 3], dets[pos:, 3])
w = np.maximum(0.0, xx2 - xx1 + 1)
h = np.maximum(0.0, yy2 - yy1 + 1)
inter = w * h
ovr = inter / (areas[i] + areas[pos:] - inter)
# Three methods: 1.linear 2.gaussian 3.original NMS
if method == 1: # linear
weight = np.ones(ovr.shape)
weight[ovr > Nt] = weight[ovr > Nt] - ovr[ovr > Nt]
elif method == 2: # gaussian
weight = np.exp(-(ovr * ovr) / sigma)
else: # original NMS
weight = np.ones(ovr.shape)
weight[ovr > Nt] = 0
dets[:, 4][pos:] = weight * dets[:, 4][pos:]
# select the boxes and keep the corresponding indexes
inds = np.argwhere(dets[:, 4] > thresh)
keep = inds.astype(int).T[0]
return keep
softnms适合于减少密集检测场景下因为nms造成的漏检,但也会增加在同一个目标上有多个检测框时的误检,如下图所示:
 左侧是nms的结果,右侧是softnms的结果。到底要不要用softnms代替nms,要根据自己的检测场景和使用nms进行过滤的效果来决定,如果是密集检测场景,nms过滤的结果存在很多的被遮挡目标的漏检,那么使用softnms可以改善检测效果。如果是非密集的检测场景,nms的检测效果是以误检为主,那么换成softnms之后的效果可能不会有提升。但终究softnms提供了一个新的思路,并且在某些特定情况下可以改善效果,其思想值得学习。
左侧是nms的结果,右侧是softnms的结果。到底要不要用softnms代替nms,要根据自己的检测场景和使用nms进行过滤的效果来决定,如果是密集检测场景,nms过滤的结果存在很多的被遮挡目标的漏检,那么使用softnms可以改善检测效果。如果是非密集的检测场景,nms的检测效果是以误检为主,那么换成softnms之后的效果可能不会有提升。但终究softnms提供了一个新的思路,并且在某些特定情况下可以改善效果,其思想值得学习。
3 SofterNMS
论文《Bounding Box Regression with Uncertainty for Accurate Object Detection》,从名字中可以看出是基于bounding box回归的方差来得到更加精确的检测结果。之所以叫做softer nms这个名字,是因为作者在arxiv上提交的第一版论文名字叫做《Softer-NMS: Rethinking Bounding Box Regression for Accurate Object Detection》,而最新的第三个版本改为了现在的名字。
1 核心思想
在检测的后处理过程nms中,是根据各检测框的置信度进行排序,保留置信度较大的检测框,抑制掉和保留框IOU较大但置信度较小的框,达到消除重复检测的目的。这里是有一个前提,置信度较大的框定位也更加准确,实际情况真的是这样吗,作者认为不是的,如下图所示:
 因此,作者就提出了在模型学习的过程中,还应该学习检测框各位置处的定位置信度,这样才能结合检测结果得到更加精确的检测结果。以faster rcnn为例,如下图所示,作者在模型训练过程中,输出了box std:
因此,作者就提出了在模型学习的过程中,还应该学习检测框各位置处的定位置信度,这样才能结合检测结果得到更加精确的检测结果。以faster rcnn为例,如下图所示,作者在模型训练过程中,输出了box std:
 上图中可以看出,模型预测了各点的定位方差之后,损失函数发生了变化,那么可以预见在模型预测过程中,推理过程也会发生变化。下面分别介绍这两部分内容。
上图中可以看出,模型预测了各点的定位方差之后,损失函数发生了变化,那么可以预见在模型预测过程中,推理过程也会发生变化。下面分别介绍这两部分内容。
1.1 模型预测值及理论基础
作者以Faster RCNN和Mask RCNN这样的两阶段检测网络为例,模型的预测值不再是anchor box相对于真实框的中心点偏移及宽高变换系数,而是改成直接预测anchor box与真实框四个顶点位置 ( x 1 , y 1 , x 2 , y 2 ) (x_1,y_1,x_2,y_2) (x1,y1,x2,y2)直接的偏差值。如下图所示:
 为了估计每个点的定位的准确度,作者认为每个预测框的坐标满足高斯分布:
为了估计每个点的定位的准确度,作者认为每个预测框的坐标满足高斯分布:

x e x_e xe表示估计的点的位置, σ \sigma σ表示估计值的标准差(确定程度), σ − > 0 \sigma -> 0 σ−>0时,表示模型特别确信自己的预测结果。
作者认为每个真实框的分布符合狄拉克delta分布,及标准差为0的高斯分布的极限:
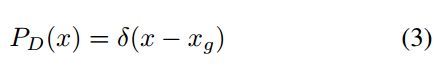
x g x_g xg为真实框的位置。
狄拉克delta分布:
下面内容来自于:https://blog.csdn.net/lanchunhui/article/details/54293415
 也就是说狄拉克delta分布在真实位置处概率值为无穷大,其余位置处概率为0。
也就是说狄拉克delta分布在真实位置处概率值为无穷大,其余位置处概率为0。
本文主要是应用狄拉克delta分布为标准差为0的高斯分布的极限这一性质,因为预测框的位置符合高斯分布,所以如果预测框的分布和真实框的分布越接近,表示模型对目标的定位越准确。但如何衡量两个分布的接近程度呢,答案就是KL散度。
1.2 KL loss
结合上面的分析,可以看到,模型训练的目的是在训练集上最小化 P Θ ( x ) P_{\Theta}(x) PΘ(x)和 P D ( x ) P_D(x) PD(x)之间的KL散度。最优参数为:

保持模型的分类损失不变,修改回归损失为两个分布的KL散度,即:
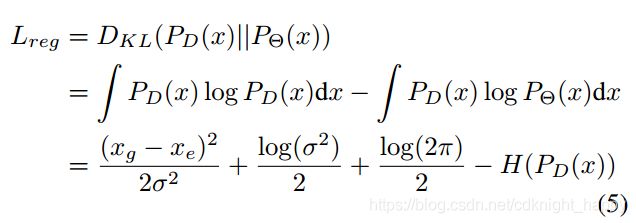

模型训练的目的是,如果位置 x e x_e xe估计的不准确,我们期望的是此时网络预测的定位标准差 σ 2 \sigma^2 σ2比较大,那么 L r e g L_{reg} Lreg应该比较大(论文中说 L r e g L_{reg} Lreg应该比较小,这是我自己理解错误吗?预测值和真实值差距大的时候,两个分布的差异比较大,KL散度不是应该更大吗?)由于 log ( 2 π ) 2 \frac{\log(2 \pi)}{2} 2log(2π)和 H ( P D ( x ) ) H(P_D(x)) H(PD(x))和估计的参数 Θ \Theta Θ无关,因此有:
 当 σ = 1 \sigma = 1 σ=1时,KL损失变为标准的欧式损失:
当 σ = 1 \sigma = 1 σ=1时,KL损失变为标准的欧式损失:
 KL损失对于定位的估计值 x e x_e xe和定位标准差 σ \sigma σ都是可微分的,有:
KL损失对于定位的估计值 x e x_e xe和定位标准差 σ \sigma σ都是可微分的,有:
 由于 σ \sigma σ位于分母上,因此可能会在训练的早期发生梯度爆炸。为了避免发生梯度爆炸,作者定义网络的预测值为 α = log ( σ 2 ) \alpha = \log(\sigma^2) α=log(σ2),因此有:
由于 σ \sigma σ位于分母上,因此可能会在训练的早期发生梯度爆炸。为了避免发生梯度爆炸,作者定义网络的预测值为 α = log ( σ 2 ) \alpha = \log(\sigma^2) α=log(σ2),因此有:
 此时有:
此时有:
∂ L r e g ∂ α = − 1 2 ( x g − x e ) 2 e − α + 1 2 = 1 2 ( 1 − ( x g − x e ) 2 e − α ) \frac{\partial L_{reg}}{\partial \alpha} = -\frac{1}{2}(x_g -x_e)^2e^{- \alpha}+\frac{1}{2} \\= \frac{1}{2}(1 - (x_g - x_e)^2e^{- \alpha}) ∂α∂Lreg=−21(xg−xe)2e−α+21=21(1−(xg−xe)2e−α)
改变预测值为 α \alpha α之后,只要模型对于 α \alpha α的预测值不为无穷大,就不会造成梯度爆炸。
由于在公式9所示的损失函数中,定义的是二阶函数,因此作者模拟L1、L2和smoothL1的关系,定义了smooth版本的KL loss:
{ e − α 2 ( x g − x e ) 2 + 1 2 α , ∣ x g − x e ∣ < 1 e − α ( ∣ x g − x e ∣ − 1 2 ) + 1 2 α , ∣ x g − x e ∣ ≥ 1 \begin{cases} \frac{e^{- \alpha}}{2}(x_g - x_e)^2 + \frac{1}{2} \alpha ,& |x_g - x_e| < 1 \\ e^{- \alpha}(|x_g - x_e| - \frac{1}{2})+ \frac{1}{2} \alpha,& |x_g - x_e| \geq 1 \end{cases} {2e−α(xg−xe)2+21α,e−α(∣xg−xe∣−21)+21α,∣xg−xe∣<1∣xg−xe∣≥1
作者对进行 α \alpha α预测的FC层使用高斯初始化,均值为0,标准差为0.0001,所以在训练的初期,KL损失等价于标准的smooth L1损失。
1.3 variance vote
在使用作者定义的网络完成预测后,可以使用相邻预测框学习的标准差进行加强来得到精确的目标位置,这就是本节所述的variance vote。
如下图所示,可以把variance vote添加到NMS或soft-NMS的迭代过程中。
 加权过程中,也是首先选取score值最大的检测框b,得到其预测信息 { x 1 , y 1 , x 2 , y 2 , s , σ x 1 , σ y 1 , σ x 2 , σ y 2 } \{x_1,y_1,x_2,y_2,s,\sigma_{x_1},\sigma_{y_1},\sigma_{x_2},\sigma_{y_2}\} {x1,y1,x2,y2,s,σx1,σy1,σx2,σy2},目标的预测框的位置是通过该框及其相邻框的加权得到的。加权系数的计算受到了soft nms的启发,某个预测框和置信度最大的框之间的IOU越大或该预测框各点处的预测不确定度越小,该预测框对于最终目标位置的贡献越大。即定义公式如下:
加权过程中,也是首先选取score值最大的检测框b,得到其预测信息 { x 1 , y 1 , x 2 , y 2 , s , σ x 1 , σ y 1 , σ x 2 , σ y 2 } \{x_1,y_1,x_2,y_2,s,\sigma_{x_1},\sigma_{y_1},\sigma_{x_2},\sigma_{y_2}\} {x1,y1,x2,y2,s,σx1,σy1,σx2,σy2},目标的预测框的位置是通过该框及其相邻框的加权得到的。加权系数的计算受到了soft nms的启发,某个预测框和置信度最大的框之间的IOU越大或该预测框各点处的预测不确定度越小,该预测框对于最终目标位置的贡献越大。即定义公式如下:
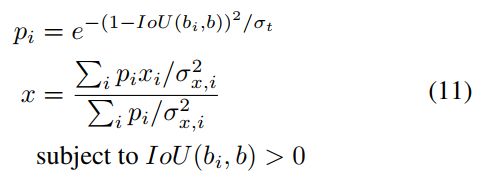 σ t \sigma_t σt是自定义的超参数。
σ t \sigma_t σt是自定义的超参数。
作者设计的加权规则,没有使用分类的置信度,而是使用IOU和预测的不确定度,下图给出了variance voting的结果。
2 实验
 消融研究证明了KL loss和var voting的效果,并且softer nms可以和soft nms结合进一步改善检测效果。
消融研究证明了KL loss和var voting的效果,并且softer nms可以和soft nms结合进一步改善检测效果。
 σ t \sigma_t σt和AP的映射关系,作者在实验中设置 σ t = 0.02 \sigma_t = 0.02 σt=0.02。
σ t \sigma_t σt和AP的映射关系,作者在实验中设置 σ t = 0.02 \sigma_t = 0.02 σt=0.02。


