后处理方法NMS、Soft-NMS、 Softer-NMS、WBC、DIoUNMS 、NMS替代算法Confluence

1、 NMS

非最大抑制（NMS）主要用于基于深度学习的目标检测模型输出的后处理，从而去除冗余的检测框，获得正确的检测结果。
算法流程：
将网络输出框集合B按照置信度分数S从高到低的顺序排序，定义D为最终检测框集合，Nt 为 NMS 阈值。
当B不为空集时：
①m为置信度分数最高的框，将m放入D，并将它从B中删除
②对于B中余下的每个框bi：
如果 $iou(m,bi)\ge N_t$，则将bi从B中删除返回检测结果D

通过分析可以发现NMS存在以下几个缺陷：
①稠密场景下漏检多：如下图1所示，当两个目标距离较近存在部分重叠时，置信度较小的目标漏检的可能性较大。

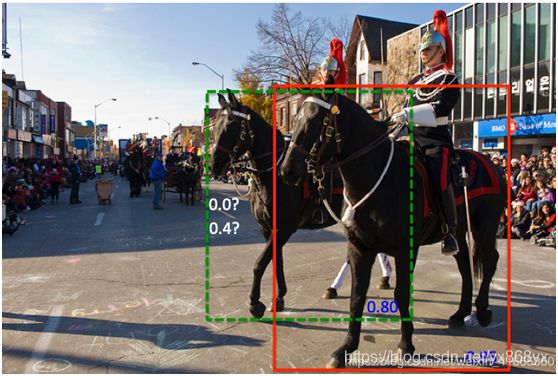
②NMS 默认置信度分数较高的框，定位更精确，由于分类和回归任务没有直接相关性，因此这个条件并不总是成立。比如图2中，置信度分数高的边界框并不总是比置信度低的框更可靠

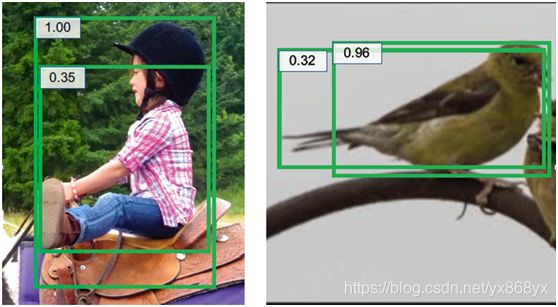
图2的(a)中两个边界框位置都不够精确；(b)中置信度较高的边界框的左边界精确度较低
③Ground Truth 的标注可能并不可靠
python代码：

import numpy as np

def nms(dets, Nt):

    x1 = dets[:,0]
    y1 = dets[:,1]
    x2 = dets[:,2]
    y2 = dets[:,3]
    scores = dets[:,4]

    order = scores.argsort()[::-1]
    #计算面积
    areas = (x2 - x1 + 1)*(y2 - y1 + 1)

    #保留最后需要保留的边框的索引
    keep = []
    while order.size > 0:
        # order[0]是目前置信度最大的，肯定保留
        i = order[0]
        keep.append(i)
        
        #计算窗口i与其他窗口的交叠的面积
        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])

        #计算相交框的面积,不相交时用0代替
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h

        #计算IOU：相交的面积/相并的面积
        ovr = inter / (areas[i] + areas[order[1:]] - inter)
        
        inds = np.where(ovr < thresh)[0]
        order = order[inds + 1]

    return keep

# test
if __name__ == "__main__":
    dets = np.array([[30, 20, 230, 200, 1],
                     [50, 50, 260, 220, 0.9],
                     [210, 30, 420, 5, 0.8],
                     [430, 280, 460, 360, 0.7]])
    thresh = 0.35
    keep_dets = nms(dets, thresh)
    print(keep_dets)
    print(dets[keep_dets])

2、 Soft-NMS

针对NMS存在的第一个问题，通过分析发现主要是因为在NMS算法中每次直接将与m的iou大于等于$N_t$的检测框直接删除导致的。因此基于NMS算法，Soft−NMS进行了如下改进：

将于m重叠的检测框置信度降低，而不是直接删除。

这样可能存在另一个问题，同一目标的其他检测框也可能被保留下来。因此需要设计合适的策略，既保留相近的其他目标，又删除重复检测的目标。直觉上可以发现通常重复的检测框具有更高的重叠，因此可以根据iou大小来设计置信度分数下降的程度。置信度修正策略如下：

该策略为iou的线性函数，同样可以使用高斯惩罚函数，将当前检测框得分乘以一个权重函数，该函数会衰减与最高得分检测框M有重叠的相邻检测框分数，越是与M框高度重叠的检测框，其得分衰减越严重，为此我们选择高斯函数为权重函数，从而修改其删除检测框的规则。

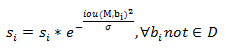
算法流程如下图所示：

红色框中的代码是 NMS 的方法，绿色框中的代码为 Soft-NMS 的实现—NMS等价于Soft-NMS的特殊情况（使用0/1惩罚项代替线性或高斯惩罚函数）
python 代码：

# -*- coding:utf-8 -*-
import numpy as np
def py_cpu_softnms(dets, Nt=0.3, sigma=0.5, thresh=0.5, method=2):
    """
    py_cpu_softnms
    :param dets:   boexs 坐标矩阵 format [x1, y1, x2, y2, score]
    :param Nt:     iou 交叠阈值
    :param sigma:  使用 gaussian 函数的方差
    :param thresh: 最后的分数阈值
    :param method: 使用的方法，1：线性惩罚；2：高斯惩罚；3：原始 NMS
    :return:       留下的 boxes 的 index
    """

    N = dets.shape[0]
    # the order of boxes coordinate is [x1,y1,x2,y2]
    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)

    for i in range(N):
        # intermediate parameters for later parameters exchange
        tB = dets[i, :4]
        ts = dets[i, 4]
        ta = areas[i]
        pos = i + 1

        if i != N-1:
            maxscore = np.max(dets[:, 4][pos:])
            maxpos = np.argmax(dets[:, 4][pos:])
        else:
            maxscore = dets[:, 4][-1]
            maxpos = -1

        if ts < maxscore:
            dets[i, :] = dets[maxpos + i + 1, :]
            dets[maxpos + i + 1, :4] = tB

            dets[:, 4][i] = dets[:, 4][maxpos + i + 1]
            dets[:, 4][maxpos + i + 1] = ts

            areas[i] = areas[maxpos + i + 1]
            areas[maxpos + i + 1] = ta

        # IoU calculate
        xx1 = np.maximum(dets[i, 0], dets[pos:, 0])
        yy1 = np.maximum(dets[i, 1], dets[pos:, 1])
        xx2 = np.minimum(dets[i, 2], dets[pos:, 2])
        yy2 = np.minimum(dets[i, 3], dets[pos:, 3])

        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        ovr = inter / (areas[i] + areas[pos:] - inter)
        
        # Three methods: 1.linear 2.gaussian 3.original NMS
        if method == 1:  # linear
            weight = np.ones(ovr.shape)
            weight[ovr > Nt] = weight[ovr > Nt] - ovr[ovr > Nt]
        elif method == 2:  # gaussian
            weight = np.exp(-(ovr * ovr) / sigma)
        else:  # original NMS
            weight = np.ones(ovr.shape)
            weight[ovr > Nt] = 0

        dets[:, 4][pos:] = weight * dets[:, 4][pos:]

    # select the boxes and keep the corresponding indexes
    inds = np.argwhere(dets[:, 4] > thresh)
    keep = inds.astype(int).T[0]

return keep

算法时间复杂度：O(n2)，其中n为待筛选检测框数量。
注意：
通过对比可以看出，原始NMS与Soft−NMS算法中的模式3等价，也就是说，删除iou过高的重叠框等价于将该重叠框置信度分数置0。

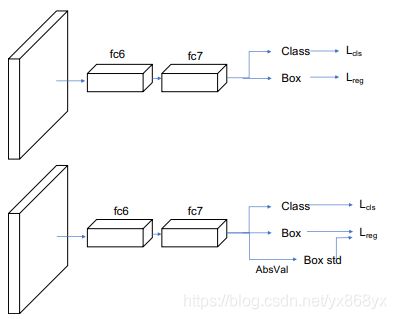
3、 Softer-NMS

Soft−NMS只解决了三个问题中的第一个问题。对于第二个问题，分类置信度分数和框的iou不是强相关，因此需要一种新的方法来衡量框的位置置信度。

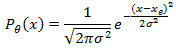
其中$\theta$为可学习参数的集合，$x_e$为被估计的边界框位置。标准差$\sigma$衡量预测的不确定性，当$\sigma \to 0$ 时，表示网络对预测的位置的置信度很高。

GT符合delta分布，即边界框置信度也可以使用高斯分布来表示，符合当$\sigma \to 0$ 时，变成 Dirac delta函数：
$P_D(x)=\delta (x-x_g)$
其中，$x_g$为GT边界框位置。
KL 损失函数:
用于具有定位置信度（localization confidence）的训练检测网络
目标定位的目标是估计参数θ ^，使N个样本的$P_{\theta }(x)$和$P_D(x)$之间的KL散度最小。


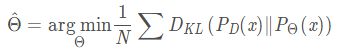
使用KL散度作为回归损失函数，对于单个样本：

分析可知，当$x_e$预测不准确时，网络预测更大的网络预测更大的${\sigma }^2$使$L_{reg}$更小。$log(2\pi /2)$和 $H(P_D(x))$与估计参数θ无关，因此


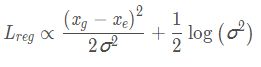
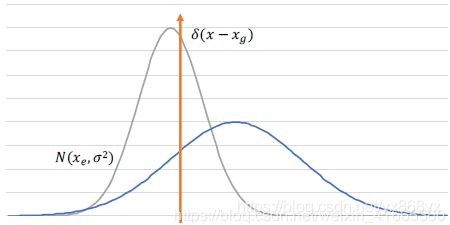
灰色曲线为估计的分布，橙色曲线为GT的Dirac delta分布。当位置$x_e$估计不准确时，网络预测更大${\sigma }^2$的使$L_{reg}$更小，蓝色曲线。
由于$\sigma$位于分母，为了防止梯度爆炸，网络预测 $\alpha =log({\sigma }^2)$代替直接预测$\sigma$。

对于$\mid x_g-x_e\mid >1$使用类似于 smooth L1损失

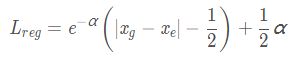
方差投票
获取预测框位置方差后，根据相邻边界框位置方差来对候选框投票。softer−NMS算法如下

蓝色和绿色分别为 Soft−NMS和 Softer−NMS
位置更新规则如下：


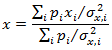
Subject to $IoU(b_i,b)>0$

通过分析发现，有两类邻近框权重较低:
① 位置方差较大的检测框
② 和选中框的iou小的框
由于分类分数较低的框可能有较高的位置置信度，因此分类置信度不参与位置投票。
NMS 主要用于去除重复的检测框。

Soft−NMS在NMS的基础上，不再直接去除重叠较高的检测框，而是将重叠的检测框的分类置信度分数降低。最终去除重复的检测框，而保留存在一定程度重叠的不同目标的检测框，该方法比较适用于稠密目标的检测。

在前两者的基础上，Softer−NMS算法对检测框的位置概率分布进行建模。对于重叠的检测框，根据重叠程度和位置不确定性进行投票，重叠程度高，位置分布方差小的检测框权重大，从而获得更精确的检测框。

4、 各种nms特点一句话总结：

nms的应用范围：只应用在前向推理的过程中，在训练中不进行此步。

pytorch源码：
https://blog.csdn.net/qq_33270279/article/details/103721790
文本检测类NMS见：
https://blog.csdn.net/xu_fu_yong/article/details/93180685

5、WBC（Weighted Box Clustering）

WBC，加权框聚类，是在Retina U-Net这篇论文中提出的一种对检测后冗余bbox进行后处理算法，也是用来删除冗余的bbox的。由于医学图像的高分辨率及3D成像（MRI），需要对patch crops进行训练，从而需要在可用GPU内存限制与batch size和patch size之间权衡。

为了合并对目标检测的预测结果，作者提出了weighted box clustering（WBC），加权框聚类：这个算法与非极大值抑制算法（NMS）类似，根据IoU阈值进行聚类的预测，而非选择得分最高的候选框。

WBC的计算
这个算法与非极大值抑制算法（NMS）类似，根据IoU阈值进行聚类的预测。
其计算公式如下：

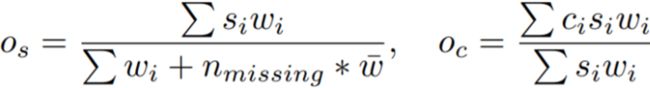
其中，$o_s$表示每个预测框的加权置信分数，$o_c$表示每个坐标的加权平均值，i是聚类的下标，s是置信度分数，c是坐标。

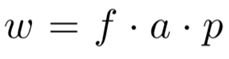
$w$是加权因子，包含：
重叠因子$f$：预测框与得分最高的框（softmax confidence）之间的重叠权重。
区域$a$：表明较大的框有较高的权重。
patch中心因子$p$：以patch中心的正态分布密度分配分数。
而对于nmissing，如下图

Prediction1、2、3是对同一张图的三张预测图，1中有两个框，相对来说，2、3中就missing了两个框，所以$n_{missing}=2$。

WBC的代码实现（来自Retina U-Net）

import numpy as np

def weighted_box_clustering(dets, box_patch_id, thresh, n_ens):
    #2D
    dim = 2 if dets.shape[1] == 7 else 3
    y1 = dets[:, 0]
    x1 = dets[:, 1]
    y2 = dets[:, 2]
    x2 = dets[:, 3]
    scores = dets[:, -3]
    box_pc_facts = dets[:, -2]
    box_n_ovs = dets[:, -1]
    #计算每个检测框的面积
    areas = (y2 - y1 + 1) * (x2 - x1 + 1)
    #3D
    if dim == 3:
        z1 = dets[:, 4]
        z2 = dets[:, 5]
        areas *= (z2 - z1 + 1)

    #按照每个框的得分（score）降序排序
    order = scores.argsort()[::-1]

    keep = []         #保留最后留下的bbox集合
    keep_scores = []  #保留最后留下的bbox的置信度集合
    keep_coords = []  #保留最后留下的bbox的坐标信息集合

    while order.size > 0:
        i = order[0]  #置信度最高的bbox的index
        #得到重叠区域
        #选择大于x1,y1和小于x2,y2的区域
        xx1 = np.maximum(x1[i], x1[order])
        yy1 = np.maximum(y1[i], y1[order])
        xx2 = np.minimum(x2[i], x2[order])
        yy2 = np.minimum(y2[i], y2[order])
        #计算重叠面积，不重叠时面积为0
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        #3D
        if dim == 3:
            zz1 = np.maximum(z1[i], z1[order])
            zz2 = np.minimum(z2[i], z2[order])
            d = np.maximum(0.0, zz2 - zz1 + 1)
            inter *= d

        #计算IoU=重叠面积/（面积1+面积2-重叠面积）
        ovr = inter / (areas[i] + areas[order] - inter)

        #获取与当前框匹配的所有预测以构建一个聚类(cluster)
        matches = np.argwhere(ovr > thresh)

        match_n_ovs = box_n_ovs[order[matches]]
        match_pc_facts = box_pc_facts[order[matches]]
        match_patch_id = box_patch_id[order[matches]]
        match_ov_facts = ovr[matches]
        match_areas = areas[order[matches]]
        match_scores = scores[order[matches]]

        #通过patch因子和大小对cluster中的所有分数进行加权
        match_score_weights = match_ov_facts * match_areas * match_pc_facts
        match_scores *= match_score_weights

        #对于权重平均值，分数必须除以当前cluster位置的预期总数。预计每个patch预测1次。因此，整体模型的数量乘以该位置处的patches的平均重叠（cluster的框可能部分位于不同重叠的区域中）。
        n_expected_preds = n_ens * np.mean(match_n_ovs)

        #获得缺失预测的数量作为补丁的数量，其不对当前聚类（cluster）做出任何预测。
        n_missing_preds = np.max((0, n_expected_preds - np.unique(match_patch_id).shape[0]))

        #对misssing的预测给出平均权重（预期预测是cluster中所有预测的平均值）。
        denom = np.sum(match_score_weights) + n_missing_preds * np.mean(match_score_weights)

        #计算聚类（cluster）的加权平均分数
        avg_score = np.sum(match_scores) / denom

        #计算聚类（cluster）坐标的加权平均值。现在只考虑现有的预测。
        avg_coords = [np.sum(y1[order[matches]] * match_scores) / np.sum(match_scores),
                      np.sum(x1[order[matches]] * match_scores) / np.sum(match_scores),
                      np.sum(y2[order[matches]] * match_scores) / np.sum(match_scores),
                      np.sum(x2[order[matches]] * match_scores) / np.sum(match_scores)]
        if dim == 3:
            avg_coords.append(np.sum(z1[order[matches]] * match_scores) / np.sum(match_scores))
            avg_coords.append(np.sum(z2[order[matches]] * match_scores) / np.sum(match_scores))

        #由于大量的缺失预测，一些聚类的分数可能非常低。用较小的阈值过滤掉，以加快评估速度。
        if avg_score > 0.01:
            keep_scores.append(avg_score)
            keep_coords.append(avg_coords)

        #保留IoU小于所设定阈值的bbox
        inds = np.where(ovr <= thresh)[0]
        order = order[inds]

    return keep_scores, keep_coords

6、DIoUNMS：

该NMS在DIoUloss一文中提出，在nms过程中采用DIoU的计算方式替换了IoU，由于DIoU的计算考虑到了两框中心点位置的信息，故使用DIoU进行评判的nms效果更符合实际，效果更优。

7、Confluence

这种方法不是只依赖单个框的得分，也不依赖IoU去除冗余的框，它使用曼哈顿距离，在一个cluster中选取和其他框都是距离最近的那个框，然后去除那些附近的高重合的框。

Confluence是一个2阶段的算法，它保留了最优边界框，并消除了假阳性。第1阶段使用置信加权曼哈顿距离来度量框之间的相关性，然后通过置信度加权，得到最优的那个框。第2阶段涉通过和这个框的交汇程度来去掉其他的假阳框。

曼哈顿距离就是L1范数，就是所有点的水平和垂直距离的和，两点之间的曼哈顿距离表示如下：

两个框之间的接近程度可以表示为左上角点和右下角点的曼哈顿距离的和：

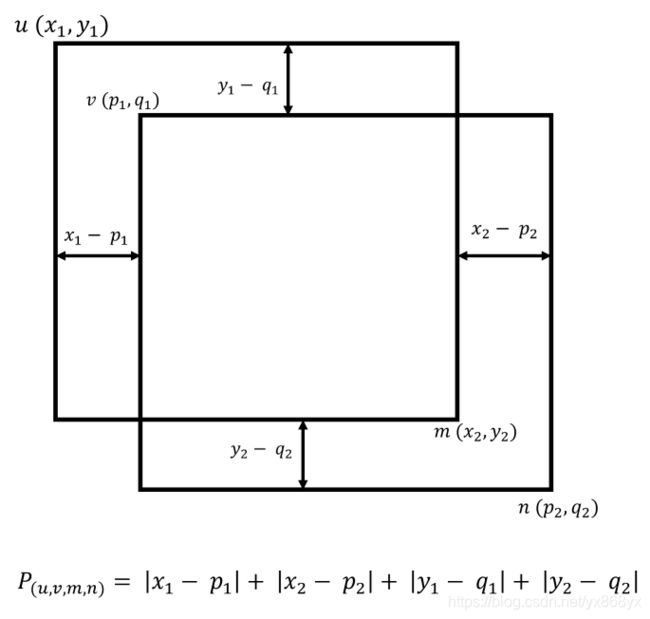
P越小表示交汇程度越高，P越大表示这两个框越不可能表示同一个物体。对于一个cluster内的框，我们把具有最小簇内的P值的框作为最佳的检测框。从图1中可以看到，Confluence具有更好的鲁棒性。

在实际使用中，由于框的尺寸不一，所以在用阈值来去除FP的时候，会对这个超参数阈值很敏感，所以需要对框进行归一化，归一化方法如下：

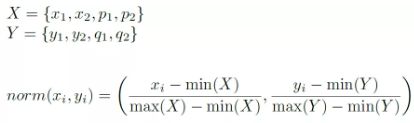
归一化之后，使得簇内的框和簇外的框可以分的很开

所有的坐标归一化到0~1之后，两个有相交的框之间的接近度量会小于2，因此，只要两个框之间的P值小于2，就属于同一个cluster，一旦cluster确定了之后，就可以找到最优的簇内框。然后，设置一个阈值，所有和这个最优框的接近度小于这个阈值的框都会去掉，然后对所有的框重复这个操作。

NMS只考虑物体的置信度得分，而Confluence会同时考虑物体的置信度得分c和p值，然后得到一个加权的接近度：

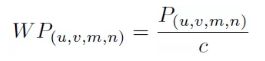
算法流程如下：

1、对所有的类别进行遍历。
2、得到对应类别的所有的检测框。
3、计算对应类别的所有检测框的两两接近度p，计算的时候使用坐标的归一化。
4、遍历对应类别中的每一个检测框，对每个检测框，把p值小于2的归到一个簇里面，并计算对应的置信度加权接近度。
5、找到一个簇里面具有最小加权p值（最优）的那个框，找到之后，保存这个框，并且将其从总的框列表里删除。
6、对于其他的所有的框，其接近度小于预设阈值的全部去除。
7、循环处理所有的框。
每个步骤的计算复杂度都为O(N)，总的Confluence的复杂度为$O(N^2)$

代码：https://github.com/Huangdebo/Confluence
参考博客：
https://www.freesion.com/article/9119880695/
https://blog.csdn.net/weixin_41665360/article/details/99818073
https://blog.csdn.net/qq_33270279/article/details/103721790
https://blog.csdn.net/qq_41084756/article/details/100600003
https://blog.csdn.net/qq_41084756/article/details/96735852
https://www.cnblogs.com/shuimuqingyang/p/14132070.html等