阿里云天池大赛工业蒸汽预测学习（3）

``最近开始了本赛题特征工程部分的学习

**概念：**特征工程就是从原始数据提取特征的过程，这些特征可以很好的描述数据，并且利用特征建立的模型在位置数据上的性能表现可以达到最优
流程
1.去掉无用特征
2.去除冗余特诊，利用存在的特征，转换特征，内容中的特征以及其他数据源生成新特征
3.对特征进行处理

赛题部分：
异常值分析

 plt.figure(figsize=(18,10))
 plt.boxplot(x=train_data.values,labels=train_data.columns)
 plt.hlines([-7.5,7.5],0,40,colors='r')
 plt.show()

这里绘制各个特征的箱线图观察数据分布。通过绘图可以看出有些数据存在明显的异常值

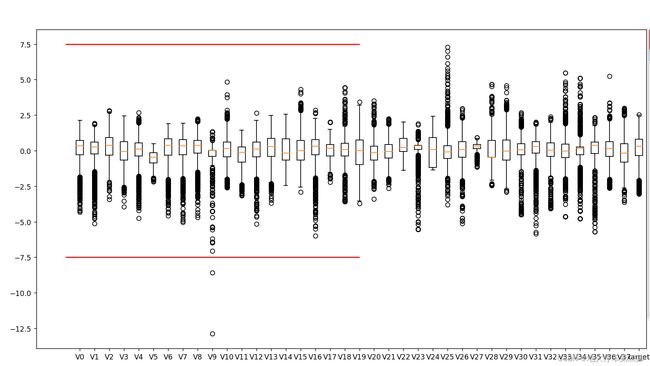
可以看出，V9中就有明显的异常值，下面将这些异常值删除。

train_data=train_data[train_data['V9']>-7.5]#每个样本含的内容都有v0~target，选取v9＞-7.5的样本
test_data=test_data[test_data['V9']>-7.5]#选取测试集中V9>7.5的样本

接下来对数据进行归一化处理

**归一化：**归一化,就是把原来数据范围缩小(或放大)到 0 和 1 的范围。
优点：
归一化后加快了梯度下降求最优解的速度，如果机器学习模型使用梯度下降法求最优解时，归一化往往非常有必要，否则很难收敛甚至不能收敛。

归一化有可能提高精度，一些分类器需要计算样本之间的距离（如欧氏距离），例如KNN。如果一个特征值域范围非常大，那么距离计算就主要取决于这个特征，从而与实际情况相悖（比如这时实际情况是值域范围小的特征更重要）。

#数据的归一化处理
features_columns=[col for col in train_data.columns if col not in ['target']]#选取V0~~V37
min_max_scaler=preprocessing.MinMaxScaler(feature_range=(0,1))
min_max_scaler=min_max_scaler.fit(train_data[features_columns])#求得train_data数据中的一些属性


train_data_scaler=min_max_scaler.transform(train_data[features_columns])#在fit的基础上，进行标准化，降维，归一化等操作
test_data_scaler=min_max_scaler.transform(test_data[features_columns])


train_data_scaler=pd.DataFrame(train_data_scaler)#转化为dataframe
train_data_scaler.columns=features_columns#改换DataFrame的索引


test_data_scaler=pd.DataFrame(test_data_scaler)
test_data_scaler.columns=features_columns
train_data_scaler['target']=train_data['target']

python提供了归一化方法。即:MinMaxScaler.fit和MinMaxScaler.transform函数。二者结合使用就可以将数据归一化。

查看数据分布前面的绘图中会发现特征变量V5,V9,V11,V17,V22,V28在训练集和测试集中的分布差异比较大，会影响模型的泛化能力，所以要删除这些特征

drop_col=6
drop_row=1
plt.figure(figsize=(5*drop_col,5*drop_row))

for i,col in enumerate(["V5","V9","V11","V17","V22","V28"]):
    ax=plt.subplot(drop_row,drop_col,i+1)
    ax=sns.kdeplot(train_data_scaler[col],color='Red',shade=True)
    ax=sns.kdeplot(test_data_scaler[col],color='Blue',shade=True)
    ax.set_xlabel(col)
    ax.set_ylabel("Frequency")
    ax=ax.legend(["train","test"])
plt.show()

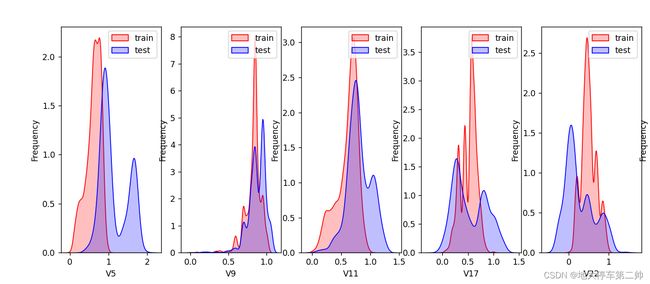
如图可以看出这些变量在训练集和测试集中区别较大
特征相关性：计算特征的相关性，以热力图的形式显示

plt.figure(figsize=(20,16))
column=train_data_scaler.columns.tolist()
mcorr=train_data_scaler[column].corr(method="spearman")
mask=np.zeros_like(mcorr,dtype=np.bool)
mask[np.triu_indices_from(mask)]=True
cmap=sns.diverging_palette(220,10,as_cmap=True)
g=sns.heatmap(mcorr,mask=mask,cmap=cmap,square=True,annot=True,fmt='0.2f')
plt.show()

DataFrame.corr（method=‘pearson’,min_periods=1)
参数pearson：Pearson相关系数来衡量两个数据集合是否在一条线上面，针对线性数据的相关系数计算，针对非线性数据会有误差。

np.zeros_like(a)函数:构建一个与a同维度的数组，初始化所有变量位0

np.triu_indices_from返回上三角矩阵的index

特征降维:
进行特征相关性筛选，筛选相关性＞0.1的特征

mcorr=mcorr.abs()
numerical_corr=mcorr[mcorr['target']>0.1]['target']
print(numerical_corr.sort_values(ascending=False))#sort排序函数，参数为false表示降序排序

多重共线性分析：
原则：特征组之间的相关性系数较大，可能存在较大的共线性影响导致模型估计不准确，因此后续要使用PCA对数据进行处理，去除多重共线性
具体相关参考：https://blog.csdn.net/weixin_45288557/article/details/111769464?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522164748951416781683914708%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=164748951416781683914708&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_alltop_positive~default-1-111769464.142^v2pc_search_insert_es_download,143^v4control&utm_term=%E5%A4%9A%E9%87%8D%E5%85%B1%E7%BA%BF%E6%80%A7&spm=1018.2226.3001.4187

多重共线性定义：在进行线性回归分析时，容易出现自变量（解释变量）之间彼此相关的现象，我们称这种现象为多重共线性

多重共线性问题就是指一个解释变量的变化引起另一个解释变量的变化。

pca=PCA(n_components=16)
new_train_pca_90=pca.fit_transform(train_data_scaler.iloc[:,0:-1])

new_test_pca_90=pca.transform(test_data_scaler)
new_train_pca_90=pd.DataFrame(new_train_pca_90)
new_test_pca_90=pd.DataFrame(new_test_pca_90)
new_train_pca_90['target']=train_data_scaler['target']
print(new_train_pca_90.describe())

保留了16个主成分

总结：本特征工程中流程
1.主要是通过箱线图查看总体数据分布寻找异常值。将异常值删除。
2.对数据进行归一化方便后续处理。
3.删除数据中训练集和测试集误差较大的数据。否则用测试集测试的时候可能会误以为模型欠拟合。
4.最后检查数据的多重共线性，通过PCA技术降维，消除多重共线性