链表：leetcode 203.移除链表元素、707.设计链表、206.反转链表

leetcode 203.移除链表元素

leetcode 707.设计链表

leetcode 206.反转链表

代码随想录算法公开课

链表理论基础

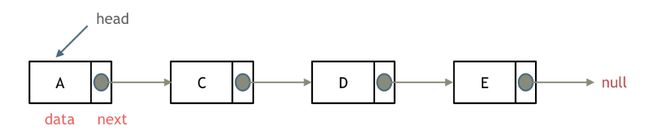
链表是一种通过指针串在一起的线性结构。链表的基本组成部分为节点，每个节点由数据域和指针域两部分组成，其中指针域存放指向下一个节点的指针，最后一个节点的指针域指向空指针。

要注意的是链表包含一个头节点（head），它是链表的入口节点。链表的结构示意图如下所示：

链表包括几种类型：

单链表

如上图所示结构的链表

双链表

双链表的每个节点含有两个指针域，分别指向上一个（prev）和下一个节点（next），它既可以向前查询也可以向后查询，双链表的结构示意图如下所示：

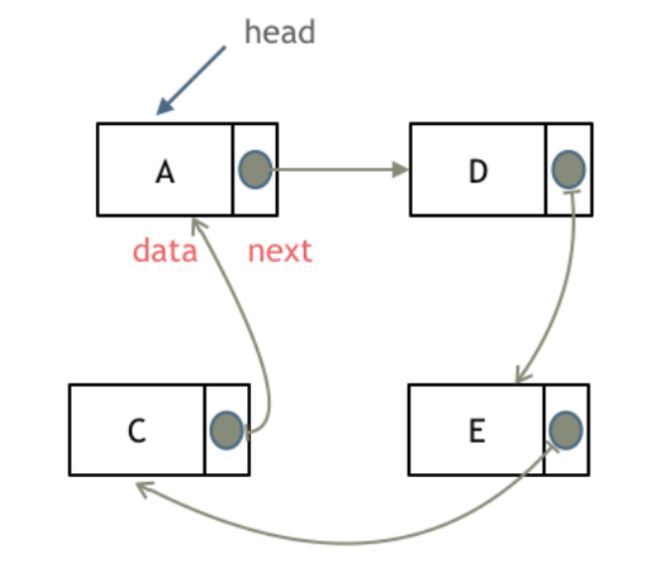
循环链表

头尾相连的链表，最后一个节点的指针域不在指向空指针Null，而是指向头节点，循环链表的结构示意图如下所示：

链表与数组的区别：

• 数组在内存中是连续分布的，链表在内存中不是连续分布的，它的节点散乱分布在内存各处。

• 由于数组内存空间连续分布，其不能增删，只能覆盖，所以对数组做增删操作的时间复杂度为O(n)；而对链表做增删操作的时间复杂度为O(1)；

• 对数组做查询操作的时间复杂度为O(1)；而对链表做查询操作的时间复杂度为O(n)；

数组在定义的时候，长度就是固定的，如果想改动数组的长度，就需要重新定义一个新的数组。

链表的长度可以是不固定的，并且可以动态增删， 适合数据量不固定，频繁增删，较少查询的场景。

链表的基本操作

定义

struct ListNode{
    int value;    // 数据域
    ListNode* next;     // 指针域
    ListNode(int x): value(x), next(NULL) {}    // 节点的构造函数
};

在定义节点时，如果不定义构造函数，那么C++会生成一个默认构造函数，但这个默认构造函数不会初始化任何成员变量。如果不自己定义构造函数而使用默认构造函数的话，在初始化时就不能直接对变量赋值：

// 自己定义构造函数
ListNode* head = new ListNode(5);

// C++生成默认构造函数
ListNode* head = new ListNode();
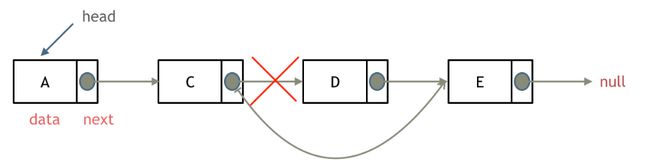
head->value = 5;

删除节点

如上图所示，要删除D节点，只需将C节点的next指针指向E节点即可，但此时D节点仍然留在内存中，C++还需手动释放这块内存。

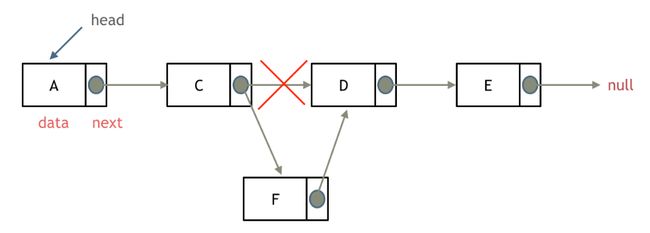
插入节点

如上图所示，要插入F节点，只需将C节点的next指针指向F节点，再将F节点的next指针指向D节点即可。

可以看出链表的增添和删除都是O(1)操作，也不会影响到其他节点。但是要注意，要是删除第五个节点，需要从头节点查找到第四个节点通过next指针进行删除操作，查找的时间复杂度是O(n)。

leetcode 203.移除链表元素

直接删除法

代码实现

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        while(head != NULL && head->val == val){    // 当要删除的是头指针时
            ListNode* tmp = head;
            head = head->next;
            delete tmp;
        }
        ListNode* cur = head;
        while(cur != NULL && cur->next != NULL){    // 当要删除的不是头指针时
            if(cur->next->val == val){
                ListNode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp;
            }
            else{
                cur = cur->next;
            }
        }
        return head;
    }
};

• 时间复杂度O(1)或O(n)

• 空间复杂度O(1)

细节处理

1. 由于题目要求删除链表中所有val的值，故使用while循环。

2. 在while循环中确保对当前作操作的节点不为NULL，否则对NULL进行操作编译器会报错。

3. C++中删除节点后要进行内存空间的释放，具体方法见代码。

4. 删除时cur所在的位置是被删节点的前一位

虚拟头结点法

代码实现

class Solution {
public:
    ListNode* removeElements(ListNode* head, int val) {
        ListNode* dummyHead = new ListNode(0);    // 虚拟头节点
        dummyHead->next = head;
        ListNode* cur = dummyHead;
        while(cur->next != NULL){
            if(cur->next->val == val){
                ListNode* tmp = cur->next;
                cur->next = cur->next->next;
                delete tmp;
            }
            else{
                cur = cur->next;
            }
        }
        head = dummyHead->next;
        delete dummyHead;
        return head;
    }
};

• 时间复杂度O(1)或O(n)

• 空间复杂度O(1)

细节处理

通过设置一个虚拟头节点，这样链表中所有元素的移除就可以按照统一的方式进行，而不需要区分头节点和其他节点。在最后删除虚拟节点时不要忘记将头节点重新赋值给dummyHead的下一个节点。

需要定义一个临时的值cur来指向虚拟头结点dummyHead，而不可直接对其进行操作，因为我们定义的链表是单向的，且最后的返回值是返回head，如果不使用临时的值代替那么最终将无法返回头节点。

leetcode 707.设计链表

代码实现

class MyLinkedList {
public:
    // 定义链表节点结构体
    struct LinkedNode {
        int val;
        LinkedNode* next;
        LinkedNode(int val):val(val), next(nullptr){}
    };

    // 初始化链表
    MyLinkedList() {
        dummyHead = new LinkedNode(0); 
        size = 0;
    }

    int get(int index) {
        if (index > (size - 1) || index < 0) {
            return -1;
        }
        LinkedNode* cur = dummyHead->next;
        while(index--){ // 如果--index 就会陷入死循环
            cur = cur->next;
        }
        return cur->val;
    }

    void addAtHead(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        newNode->next = dummyHead->next;
        dummyHead->next = newNode;
        size++;
    }

    void addAtTail(int val) {
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = dummyHead;
        while(cur->next != nullptr){
            cur = cur->next;
        }
        cur->next = newNode;
        size++;
    }

    void addAtIndex(int index, int val) {

        if(index > size) 
            return;
        if(index < 0) 
            index = 0;        
        LinkedNode* newNode = new LinkedNode(val);
        LinkedNode* cur = dummyHead;
        while(index--) {
            cur = cur->next;
        }
        newNode->next = cur->next;
        cur->next = newNode;
        size++;
    }

    void deleteAtIndex(int index) {
        if (index >= _size || index < 0) {
            return;
        }
        LinkedNode* cur = dummyHead;
        while(index--) {
            cur = cur ->next;
        }
        LinkedNode* tmp = cur->next;
        cur->next = cur->next->next;
        delete tmp;
        size--;
    }

private:
    int size;
    LinkedNode* dummyHead;

};

细节处理

仍然使用虚拟头节点思路，将链表中元素的插入、移除、查找等按同样的思路进行。

注意增删操作时的临时值cur指向将要被进行操作的节点的前一个节点（链表为单向）；而查找操作时临时值cur指向将要被进行操作的节点。总体思路不难理解。

leetcode 206.反转链表

双指针法

代码实现

class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* temp;    // 临时指针
        ListNode* cur = head; // 当前位置
        ListNode* pre = NULL; // 设为当前位置的前一个位置，初始为NULL
        while(cur){
            temp = cur->next;
            cur->next = pre;
            pre = cur;
            cur = temp;
        }
        return pre;
    }
};

• 时间复杂度O(n)

• 空间复杂度O(1)

细节处理

1. while中的循环条件：当cur指向原尾节点而pre指向尾节点的前一个节点时，还需要进行反转指向操作，操作完成后cur为“空节点”，pre指向NULL，此时不需要再进行操作，故while的循环条件为cur不为空节点。

2. 在反转操作时，由于反转后cur指向pre，而cur->next节点此时与cur失去了联系，故需要定义一个临时节点temp始终指向cur->next节点，以便对cur节点进行移动到下一个节点的操作。

递归法

代码实现

class Solution {
public:
    ListNode* reverse(ListNode* pre,ListNode* cur){
        if(cur == NULL) return pre;
        ListNode* temp = cur->next;
        cur->next = pre;
        return reverse(cur,temp);
    }
    ListNode* reverseList(ListNode* head) {
        return reverse(NULL, head);
    }

};

• 时间复杂度O(n)

• 空间复杂度O(1)

细节处理

递归法的实质仍然是双指针法