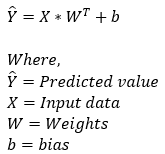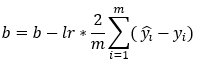梯度下降系列博客:3、批量梯度下降代码实战
- 梯度下降系列博客:1、梯度下降算法基础
- 梯度下降系列博客:2、梯度下降算法背后的数学直觉
- 梯度下降系列博客:3、批量梯度下降代码实战
- 梯度下降系列博客:4、小批量梯度下降算法代码实战
- 梯度下降系列博客:4、随机梯度下降算法代码实战
介绍:
欢迎来到梯度下降系列的结局!在这篇博客中,我们将深入研究梯度下降算法。我们将讨论梯度下降算法的所有有趣风格以及它们在 Python 中的代码示例。我们还将根据每个算法中执行的计算次数来检查算法之间的差异。我们今天不遗余力,因此我们要求您在阅读文档时运行Python文件;这样做将使您对该主题有更准确的理解,从而看到它的实际应用。让我们开始吧!
批量梯度下降:
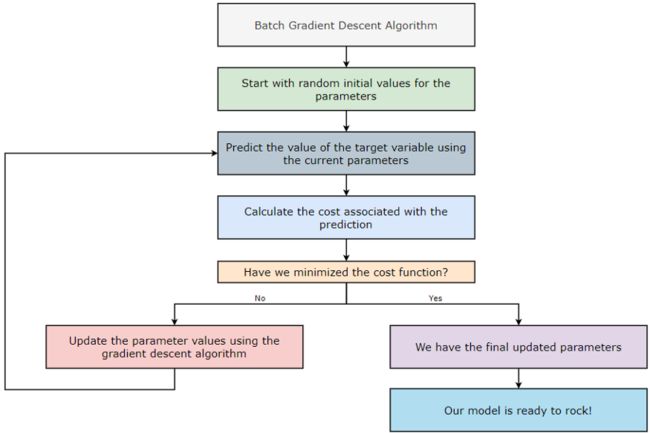
批量梯度下降 (BGD) 算法的工作原理
批量梯度下降 (BGD) 算法考虑了每次迭代中的所有训练示例。如果数据集包含大量训练示例和大量特征,则实施批量梯度下降 (BGD) 算法的计算成本会很高——所以请注意预算!让我们举个例子来更好地理解它。
批量梯度下降(BGD):
每次迭代的训练样本数量 = 100 万 = 1⁰⁶
迭代次数 = 1000 = 1⁰³
参数数量待训练 = 10000 = 1⁰⁴
总计算量 = 1⁰⁶ * 1⁰³* 1⁰⁴ = 1⁰¹³
现在,让我们看看批量梯度下降 (BGD) 算法是如何实现的。
1. 第 1 步:
首先,我们从 GitHub 存储库下载数据文件。
#Fetch the data file from GitHub repository:
!wget https://raw.githubusercontent.com/Pratik-Shukla-22/Gradient-Descent/main/Advertising.csv
2. 第 2 步:
接下来,我们导入一些必需的库来读取、操作和可视化数据。
导入所需的库
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
3. 第 3 步:
接下来,我们正在读取数据文件,然后打印它的前五行。
#Read the data file:
data = pd.read_csv("Advertising.csv")
data.head()
#Output:
index,Unnamed: 0,TV,radio,newspaper,sales
0,1,230.1,37.8,69.2,22.1
1,2,44.5,39.3,45.1,10.4
2,3,17.2,45.9,69.3,9.3
3,4,151.5,41.3,58.5,18.5
4,5,180.8,10.8,58.4,12.9
4. 第 4 步:
接下来,我们将数据集划分为特征和目标变量。
#Define the feature and target variables:
X = data[["TV","radio","newspaper"]]
Y = data["sales"]
5. 第 5 步:
为了在进一步的步骤中执行矩阵计算,我们需要重塑目标变量。
#Reshape the data in Y:
Y = np.asarray(Y)
Y = np.reshape(Y,(Y.shape[0],1))
6. 第 6 步:
接下来,我们正在规范化数据集。
#Reshape the data in Y:
Y = np.asarray(Y)
Y = np.reshape(Y,(Y.shape[0],1))
7. 第 7 步:
接下来,我们获取bias和weights矩阵的初始值。我们将在执行前向传播时在第一次迭代中使用这些值。
#Function to get intial weights and bias:
def initialize_weights(n_features):
bias = np.random.random(1)
weights = np.random.random(n_features)
#Reshape the bias and weights:
bias = np.reshape(bias,(1,1))
weights = np.reshape(weights, (1,X.shape[1]))
return bias,weights
8. 第 8 步:
接下来,我们执行前向传播步骤。此步骤基于以下公式。
#Predict the value of target variable based on the random weights: def predict(bias, weights, X): predicted_value = bias+np.dot(X,weights.T) return predicted_value
9. 第 9 步:
接下来,我们将计算与我们的预测相关的成本。此步骤基于以下公式。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kO3HJ67n-1675607637619)(null)]
#Calculate the cost:
def calculate_cost(Y, Y_pred):
error = Y_pred - Y
cost = np.sum((error)**2)/len(error)
return cost
10. 第 10 步:
接下来,我们使用梯度下降算法更新权重和偏差的参数值。此步骤基于以下公式。请注意,我们不对权重值求和的原因是我们的权重矩阵不是1*1矩阵。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-G9hiOXwM-1675607637565)(null)]
#Update the parameter values:
def update_parameters(X,Y,Y_pred,bias,weights,lr):
#Calculating the gradients:
db = (np.sum(Y_pred-Y)*2)/len(Y)
dw = (np.dot((Y_pred-Y).T,X)*2)/len(Y)
#Updating the parameters:
bias = bias - lr*db
weights = weights - lr*dw
#Return the updated parameters:
return bias, weights
维度:db = sum(200, 1) = (1, 1)
维度:dw = (1, 200) * (200, 3) = (1, 3)
维度:偏差 = (1, 1) & 权重 = (1, 3)
11. 第 11 步:
接下来,我们将使用刚刚定义的所有函数来运行梯度下降算法。我们还创建了一个空列表cost_list,用于存储所有迭代的成本值。该列表将用于在进一步的步骤中绘制图表。
#The main function to run the gradient descent algorithm:
def run_batch_gradient_descent(X,Y,lr,iter):
#Create an empty list to store cost values:
cost_list = []
#Get the initial values of weights and bias:
bias, weights = initialize_weights(X.shape[1])
for i in range(iter):
#Predict the value of the target variable:
Y_pred = predict(bias, weights, X)
#Calculate the cost associated with prediction:
cost = calculate_cost(Y, Y_pred)
#Append the cost to the list:
cost_list.append(cost)
#Update the parameters using gradient descent:
bias, weights = update_parameters(X,Y,Y_pred,bias,weights,lr)
#Return the cost list:
return bias,weights,cost_list
12. 第 12 步:
接下来,我们实际上是在调用函数来获取最终结果。请注意,我们运行的是200 iterations. 此外,我们在这里指定了learning rate of 0.01.
# 运行批量梯度下降算法 200 次迭代
bias,weights,cost = run_batch_gradient_descent(X,Y,lr=0.01,iter=200)
13. 第 13 步:
接下来,我们正在绘制 的图形iterations vs. cost
#Plot the graph of iter. vs cost:
plt.title("Iterations vs. Cost")
plt.xlabel("Iterations")
plt.ylabel("MSE cost")
plt.plot(cost,label="Batch Gradient Descent")
plt.legend()
plt.show()
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nJvPnOyB-1675607637581)(null)]
14. 第 14 步:
接下来,我们在final weights完成所有迭代后打印值。
# 在 200 次迭代后打印权重的最终值
#Print the final values of weights:
print("Weights=",weights)
#Output:
Weights= [[3.86955149 2.68445343 0.10103371]]
15. 第 15 步:
接下来,我们在final bias完成所有迭代后打印值。
#Print the final value of bias:
print("Bias=",bias)
#Output:
Bias= [[11.1441885]]
在 200 次迭代后打印偏差的最终值
16. 第 16 步:
接下来,我们绘制两个具有不同学习率的图,以查看学习率在优化中的影响。在下图中,我们可以看到学习率较高(0.01)的图比学习率较慢的图收敛得更快(0.001)。正如我们在梯度下降系列的第 1 部分中了解到的那样,这是因为学习率较低的图采用较小的步长。
#Run the gradient descent algorithm:
bias1, weights1, cost1 = run_batch_gradient_descent(X,Y,lr=0.01,iter=1000)
bias2, weights2, cost2 = run_batch_gradient_descent(X,Y,lr=0.001,iter=1000)
#Plot the graphs:
plt.title("Iterations vs. Cost")
plt.xlabel("Iterations")
plt.ylabel("MSE cost")
plt.plot(cost1,label="LR=0.01")
plt.plot(cost2,label="LR=0.001")
plt.legend()
plt.show()
绘制不同学习率的批量梯度下降算法图
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-457s3sM9-1675607637600)(null)]
17. 第 17 步:
让我们把它们放在一起。
#Fetch the data file from GitHub repository:
!wget https://raw.githubusercontent.com/Pratik-Shukla-22/Gradient-Descent/main/Advertising.csv
#Import the required libraries:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#Read the data file:
data = pd.read_csv("Advertising.csv")
print(data.head())
#Define the feature and target variables:
X = data[["TV","radio","newspaper"]]
Y = data["sales"]
#Reshape the data in Y:
Y = np.asarray(Y)
Y = np.reshape(Y,(Y.shape[0],1))
#Normalize the data:
X = (X - X.mean())/X.std()
Y = Y - Y.mean()/Y.std()
#Function to get intial weights and bias:
def initialize_weights(n_features):
bias = np.random.random(1)
weights = np.random.random(n_features)
#Reshape the bias and weights:
bias = np.reshape(bias,(1,1))
weights = np.reshape(weights, (1,X.shape[1]))
return bias,weights
#Predict the value of target variable based on the random weights:
def predict(bias, weights, X):
predicted_value = bias+np.dot(X,weights.T)
return predicted_value
#Calculate the cost:
def calculate_cost(Y, Y_pred):
error = Y_pred - Y
cost = np.sum((error)**2)/len(error)
return cost
#Update the parameter values:
def update_parameters(X,Y,Y_pred,bias,weights,lr):
#Calculating the gradients:
db = (np.sum(Y_pred-Y)*2)/len(Y)
dw = (np.dot((Y_pred-Y).T,X)*2)/len(Y)
#Updating the parameters:
bias = bias - lr*db
weights = weights - lr*dw
#Return the updated parameters:
return bias, weights
#The main function to run the gradient descent algorithm:
def run_batch_gradient_descent(X,Y,lr,iter):
#Create an empty list to store cost values:
cost_list = []
#Get the initial values of weights and bias:
bias, weights = initialize_weights(X.shape[1])
for i in range(iter):
#Predict the value of the target variable:
Y_pred = predict(bias, weights, X)
#Calculate the cost associated with prediction:
cost = calculate_cost(Y, Y_pred)
#Append the cost to the list:
cost_list.append(cost)
#Update the parameters using gradient descent:
bias, weights = update_parameters(X,Y,Y_pred,bias,weights,lr)
#Return the cost list:
return bias,weights,cost_list
#Run the gradient descent algorithm:
bias,weights,cost = run_batch_gradient_descent(X,Y,lr=0.01,iter=200)
#Print the final values of weights:
print("Weights=",weights)
#Print the final value of bias:
print("Bias=",bias)
#Plot the graph of iter. vs cost:
plt.title("Iterations vs. Cost")
plt.xlabel("Iterations")
plt.ylabel("MSE cost")
plt.plot(cost,label="Batch Gradient Descent")
plt.legend()
plt.show()
#Run the gradient descent algorithm:
bias1, weights1, cost1 = run_batch_gradient_descent(X,Y,lr=0.01,iter=1000)
bias2, weights2, cost2 = run_batch_gradient_descent(X,Y,lr=0.001,iter=1000)
#Plot the graphs:
plt.title("Iterations vs. Cost")
plt.xlabel("Iterations")
plt.ylabel("MSE cost")
plt.plot(cost1,label="LR=0.01")
plt.plot(cost2,label="LR=0.001")
plt.legend()
plt.show()
计算次数:
现在,让我们统计一下批量梯度下降算法中执行的计算次数。
**偏差:(**训练示例)x(迭代)x(参数)= 200 * 200 * 1 = 40000
**权重:(**训练示例)x(迭代)x(参数)= 200 * 200 * 3 = 120000
源码:
以上所有代码请关注wx: 猛男技术控
回复梯度下降 即可获取