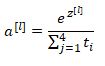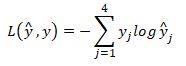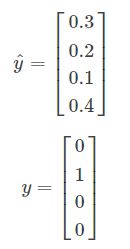2-3 Coursera吴恩达《改善深度神经网络》第三周课程笔记-超参数调试、Batch正则化和编程框架

上节课2-2 Coursera吴恩达《改善深度神经网络》第二周课程笔记-优化算法我们主要介绍了深度神经网络的优化算法。包括对原始数据集进行分割，使用mini-batch 梯度下降（mini-batch gradient descent），然后介绍了指数加权平均（Exponentially weighted averages）的概念以及偏移校正（bias correction）方法。接着，我们着重介绍了三种常用的加速神经网络学习速度的三种算法：动量梯度下降、RMSprop和Adam算法。其中，Adam结合了动量梯度下降和RMSprop各自的优点，实际应用中表现更好。然后，我们介绍了另外一种提高学习速度的方法：learning rate decay，通过不断减小学习因子，减小步进长度，来减小梯度振荡。最后，我们对深度学习中局部优化（local optima）的概念作了更深入的解释。本节课，我们将重点介绍三个方面的内容：超参数调试、Batch正则化和深度学习编程框架。

目录

《3.1调整过程》1. Tuning Process

《3.2 为超参数选择合适的范围》Using an appropriate scale to pick hyperparameters

《3.3 超参数调试实践：Pandas VS Caviar》Hyperparameters tuning in practice: Pandas vs. Caviar

《3.4 归一化网络的激活函数》Normalizing activations in a network

《3.5 将Batch Norm拟合进神经网络》Fitting Batch Norm into a neural network

《3.6 Batch Norm为什么奏效？》Why does Batch Norm work？

《3.7 测试时的 Batch Norm》Batch Norm at test time

《3.8 Softmax 回归》Softmax Regression

《3.9 训练一个Softmax分类器》Training a softmax classifier

《3.10 深度学习框架》Deep learning frameworks

《3.11 TensorFlow》TensorFlow

Summary

《3.1调整过程》1. Tuning Process

在训练神经网络时，超参数的调试十分重要，下面分享一些指导原则。

Andrew认为学习率α是需要调试的最重要的超参数。 通常来说，①学习因子α是最重要的超参数，也是需要重点调试的超参数。②动量梯度下降因子beta、各隐藏层神经元个数hidden units和mini-batch size的重要性仅次于alpha。③然后就是神经网络层数layers和学习因子下降参数learning rate decay。④最后，Adam算法的三个参数bata1,bata2,sigma一般常设置为0.9，0.999和10^-8，不需要反复调试。当然，这里超参数重要性的排名并不是绝对的，具体情况，具体分析。

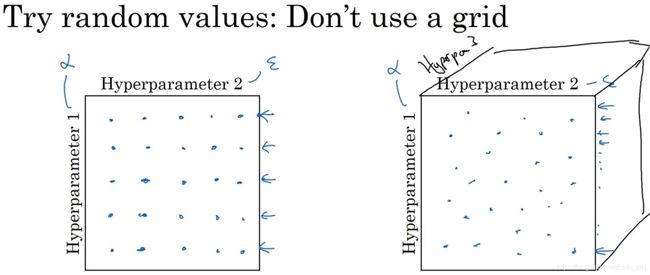
如果你尝试调整一些超参数，该如何选择调试值？常见的做法是在网格中取样（均匀间隔），如果你有两个超参数，这里放置的是5*5的网络（下图左），你可以尝试所有的25个点，然后选择效果最好的参数。当参数的数量相对较少时，这个方法很实用。

在深度学习领域，Andrew推荐随机选择点。例如超参数1是学习率α，超参数2是Adam算法分母中的ε，这种情况下α的取值很重要，而ε取值则无关紧要。如果采用上述方法，你能试验的α只有5个；但是如果你随机取值，可以试验25个独立的α，似乎你更可能发现效果更好的那个。（上图右）这是两个参数的情况，如果超参数不止两个，你搜索的是一个立方体，在三维立方体中取值，三个超参数都可以试验大量的更多的值。（下图右）

实践中，你搜索的可能不止三个超参数有时很难预知，哪个是最重要的超参数，对于你的具体应用而言，随机取值（sampling at random）而不是网格取值（sampling in the grid）表明，可以探究了更多重要超参数的潜在值，无论结果是什么。

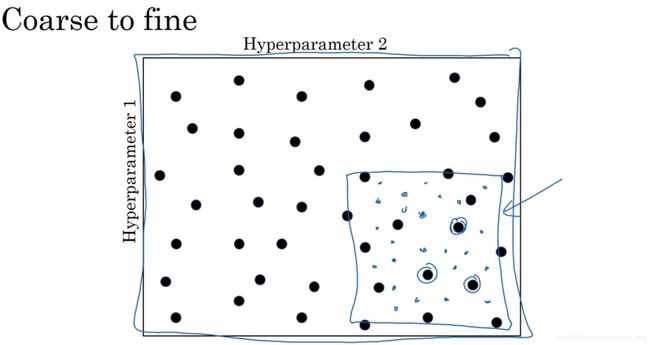
在超参数取值时，另一个惯例是采用由粗糙到精细的策略（coarse to fine sampling scheme）：

就是放大表现较好的区域（小蓝色方框内），再对此区域做更密集的随机采样。

总结，通过试验超参数的不同取值，你可以选择对训练集目标而言的最优值，或对于开发集而言的最优值，或在超参搜索过程中你最想优化的东西。

Andrew希望，这能提供一种方法去系统地组织超参数搜索过程。另一个关键点是随机取值（random sampling）和精确搜索（adequate search），考虑使用由粗糙（coarse）到精细（fine）的搜索过程。但超参数的搜索内容还不止这些，在下一个视频中，会继续讲解关于如何选择超参数取值的合理范围。

《3.2 为超参数选择合适的范围》Using an appropriate scale to pick hyperparameters

在上一个视频中，你已经看到了在超参数范围中，随机取值可以提升你的搜索效率。但随机取值（sampling at random）并不是在有效范围内的随机均匀取值，而是选择合适的标尺，用于探究这些超参数，这很重要。对于某些超参数（隐藏单元的数量或者神经网络的层数）是可以进行尺度均匀采样的，它们都是正整数，是可以进行均匀随机采样的（即超参数每次变化的尺度都是一致的），这是合理的：

但是某些超参数需要选择不同的合适尺度进行随机采样。假设你在搜索超参数α（学习速率），假设你怀疑其值最小是0.0001或最大是1。如果你画一条从0.0001到1的数轴，沿其随机均匀取值，那90%的数值将会落在0.1到1之间，结果就是，在0.1到1之间，应用了90%的资源，而在0.0001到0.1之间，只有10%的搜索资源，这看上去不太对。反而，用对数标尺搜索超参数的方式会更合理，因此这里不使用线性轴，分别依次取0.0001，0.001，0.01，0.1，1，在对数轴上均匀随机取点，这样，在0.0001到0.001之间，就会有更多的搜索资源可用，还有在0.001到0.01之间等等。如下图：

般解法是，如果线性区间为[a, b]，令m=log(a)，n=log(b)，则对应的log区间为[m,n]。对log区间的[m,n]进行随机均匀采样，然后得到的采样值r，最后反推到线性区间，即10^r。10^r就是最终采样的超参数。相应的Python语句为：

m = np.log10(a)

n = np.log10(b)

r = np.random.rand()

r = m + (n-m)*r

r = np.power(10,r)

除了α之外，动量梯度因子β（用于计算指数的加权平均数）的取值也是一样，在超参数调试的时候也需要进行非均匀采样，因为当β越接近1时，所得结果的灵敏度（sensitivity）会变化，即使只有微小的变化，所以需要更加密集地取值。一般β的取值范围在[0.9, 0.999]之间，那么1−β的取值范围就在[0.001, 0.1]之间。那么直接对1−β在[0.001, 0.1]区间内进行log变换即可，如下图：

总结，上述讲解希望能帮助你选择合适的标尺，来给超参数取值。如果你没有在超参数选择中作出正确的标尺决定，别担心，即使你在均匀的标尺上取值，如果数值总量较多的话，你也会得到还不错的结果，尤其是应用从粗到细的搜索方法，在之后的迭代中，你还是会聚焦到有用的超参数取值范围上。希望这会对你的超参数搜索有帮助，下一个视频中，我们将会分享一些关于如何组建搜索过程的思考，希望它能使你的工作更高效。

《3.3 超参数调试实践：Pandas VS Caviar》Hyperparameters tuning in practice: Pandas vs. Caviar

在结束关于超参数搜索的讨论之前，Andrew最后分享一些建议和技巧，关于如何组超参数搜索过程。如今的深度学习（deep learning）已经应用到许多不同的领域，某个应用领域的超参数设定，有可能通用于另一领域，不同的应用领域出现相互交融。比如，我曾经看到过计算机视觉领域中涌现的巧妙方法，比如说Confonets或ResNets，这我们会在后续课程中讲到。它还成功应用于语音识别（speech），我还看到过最初起源于语音识别的想法成功应用于NLP等等。

深度学习领域中，发展很好的一点是，不同应用领域的人们会阅读越来越多其它研究领域的文章，跨领域（cross-fertilization）去寻找灵感。Andrew建议，或许只是重新测试或评估你的超参数，至少每隔几个月一次，以确保你对数值依然很满意。

最后，关于如何搜索超参数的问题，我见过大概两种重要的思想流派（two major schools of thought）或人们通常采用的两种重要但不同的方式（two major different ways）。

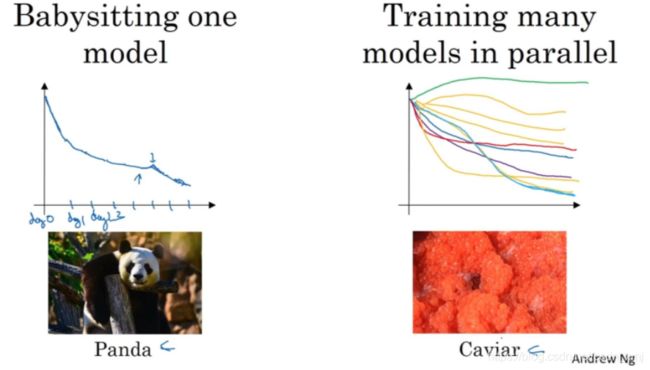
一种是照看一个模型（babysit one model），通常有庞大的数据组，但是没有许多计算资源或足够的CPU和GPU，这样的话一次试验一个模型或者一小批模型，然后每天花时间观察它，不断调整参数。总之，这是一个人们照料一个模型的方法，观察它的表现，耐心地调试学习率，但那通常是因为没有足够的计算能力（enough computational capacity），不能在同一时间试验大量模型时才采取的办法。（上图左）

另一种方法则是同时试验多种模型（training many models in parallel），已经设置了一些超参数，让它自己运行，或者是一天甚至多天，然后会获得像这样的学习曲线（learning curve），这可以是损失函数J（cost function ）或训练误差的损失（cost of your training error）或数据误差的损失（cost of your data set error），但都是曲线轨迹的度量（metric）。同时你可以开始一个有着不同超参数设定的不同模型，所以，你的第二个模型会生成一个不同的学习曲线，也许是像这样的一条（紫色曲线）。与此同时，你可以试验第三种模型，其可能产生一条像这样的学习曲线（红色曲线），还有另一条（绿色曲线），等等。或者你可以同时平行试验许多不同的模型，橙色的线就是不同的模型。用这种方式可以试验许多不同的参数设定，然后只是最后快速选择工作效果最好的那个。（上图右）

类比来看，Andrew把左边的方法称为熊猫方式（panda approach）；右边称之为鱼子酱方式（caviar strategy）。

总结，这两种方式的选择，是由你拥有的计算资源决定的，如果你拥有足够的计算机去平行试验许多模型，那绝对采用鱼子酱方式，尝试许多不同的超参数，看效果怎么样。但在一些应用领域，比如在线广告设置和计算机视觉应用领域，那里的数据太多了，你需要试验大量的模型，所以同时试验大量的模型是很困难的，它的确是依赖于应用的过程，所以会使用熊猫方式，一次照看一个模型。

所以希望你能学会如何进行超参数的搜索过程，现在，还有另一种技巧，能使神经网络变得更加坚实，它并不是对所有的神经网络都适用，但当适用时，它可以使超参数搜索变得容易许多并加速试验过程，在下个视频中将讲解这个技巧。

《3.4 归一化网络的激活函数》Normalizing activations in a network

在深度学习兴起后，最重要的一个思想是它的一种算法，叫做Batch归一化（Batch Normalization），由Sergey loffe和Christian Szegedy两位研究者创造。Batch归一化会使参数搜索问题变得很容易，使神经网络对超参数的选择更加稳定，超参数的范围会更加庞大，工作效果也很好，也会是你的训练更加容易，甚至是深层网络。下面具体看Batch归一化：

在训练之前的logistic回归模型时（如上图：左上），归一化输入特征可以加快学习过程，可以把问题的轮廓从很长的东西变成更圆的东西，易于算法优化。那么更深的模型呢？（如上图：左下）不仅有输入特征还有激活值a。既然归一化特征输入可以更有效的训练w和b，那么能否归一化a值，以更快的速度训练w和b？这就是Batch归一化的作用。实践中，通常是归一化z，下面是Batch归一化的使用方法：

假设有隐藏单元值z^(1)到z^(m)，实际上写成z^[l](i)会更准确，但是为了书写方便，省略l以便简化符号，所以这些都是针对l层的计算。如上图，用常用公式计算第l层的均值和方差，然后规范化每个z^(i)，这样z的每一个分量的都含有平均值0和方差1，但是不希望隐藏单元总是平均值0和方差1，也许不同的分布会有意义，所以计算下个公式：

其中，γ和β是模型的学习参数（learnable parameters），可以使用梯度下降算法或者Momentum、Nesterov、Adam等更新它们，就像更新神经网络的权重一样。注意γ和β的作用是，可以随意设置均值和方差，同时保证隐藏的单元已经使均值和方差标准化（standardized mean and variance）。

所以，归一化输入特征是怎样有助于神经网络中的学习，Batch归一化的作用是它适用的归一化过程，不只是输入层（input layer），甚至同样适用于神经网络中的深度隐藏层（hidden layer）。应用Batch归一化了一些隐藏单元值中的平均值和方差，不过训练输入和这些隐藏单元值的一个区别是，你也许不想隐藏单元值必须是平均值0和方差1。

下个视频将介绍如何将Batch归一化与神经网络甚至是深度神经网络相匹配。

《3.5 将Batch Norm拟合进神经网络》Fitting Batch Norm into a neural network

上个视频看到在单一隐藏层进行Batch归一化，下面看怎样在深度网络训练中拟合：

假设这样一个神经网络，可以认为每个单元负责两件事情：先计算z，然后应用到激活函数中计算a，每个圆圈代表两步的计算过程。（如上图）使用Batch归一化，将z^[1]的值进行Batch归一化，简称BN，此过程由γ^[1]和β^[1]两个参数控制，这一操作之后得到新规范化的z^[1]，然后将其输入激活函数中得到a^[1]。这是第一层的计算，Batch归一化发生在z和a之间。接下来应用a^[1]计算z^[2]，此过程由W^[2]和b^[2]两个参数控制，接着对z^[2]进行Batch归一化，此过程由γ^[2]和β^[2]两个参数控制，得到新规范化的z^[2]（z^[2]~），再计算a^[2]等等。注意一下，这里归一化学习参数β^[1]、β^[2]和Momentum、Adam、RMSprop算法中的β不同。所以，这是算法的新参数，可以使用任何一种优化算法（例如梯度下降法）来执行它。

如果使用的是深度学习编程框架（Deep Learning Programming Framework），通常你不必自己把Batch归一化步骤应用于Batch归一化层。因此，探究框架，可写成一行代码，比如说，在TensorFlow框架中，你可以用这个函数（tf.nn.batch_normalization）来实现Batch归一化，我们稍后讲解。

实践中，Batch归一化通常和训练集的mini-batch一起使用，如下图：

使用第一个mini-batchX^{1}，然后计算z^[1]；接着，第二个mini-batchX^{2}，Batch归一化会减去均值，除以标准差，由γ^[1]和β^[1]重新缩放，得到新规范化的z^[1]（z^[1]~）。注意一个细节，mini-batch进行归一化，要由γ和β重新缩放，这意味着无论b^[l]的值为多少，都会被减去，因此在使用Batch归一化时，可以消除这个参数，或者设置为0。后续重新缩放时用到β^[l]，这是一个控制参数，会影响转移或者偏置条件（the shift or the biased terms）。

总结一下关于如何用Batch归一化来应用梯度下降法：

如上图，运行for循环，①在mini-batch上应用正向传播，每个隐藏层都应用正向传播，使用Batch归一化。②然后反向传播计算梯度（这部分去掉b）。③最后更新这些参数。除了传统的梯度下降算法之外，还可以使用我们之前介绍过的动量梯度下降、RMSprop或者Adam等优化算法。

下一个视频，详细讨论Batch归一化为何效果如此显著，它到底在做什么。

《3.6 Batch Norm为什么奏效？》Why does Batch Norm work？

为什么Batch归一化会起作用呢？

一个原因是，联想输入特征归一化，输入特征值归一化后获得类似范围的值，可以加速学习。这只是冰山一角，还有更深层的原理。一起看看吧。

Batch归一化有效的第二个原因是，它可以使权重比你的网络更滞后或更深层，比如，第10层的权重更能经受得住变化，相比于神经网络中前层的权重，比如第1层，为了解释清楚，让我们来看看这个最生动形象的例子。

如上图，假如用一个浅层神经网络（类似逻辑回归）来训练识别猫的模型。假设在所有黑猫的图像上训练了数据集，现在对有色猫进行测试，正样本（positive examples）不只是左边的黑猫，还有右边其他颜色的猫，这样测试的效果可能不好。所以使你数据分布改变叫做协变量转移（covariate shift），想法是这样的，如果你已经学习了x到y的映射，如果x的分布改变了，那么你可能需要重新训练你的学习算法。

这种训练样本（黑猫）和测试样本（猫）分布的变化也是协变量转移（covariate shift）。

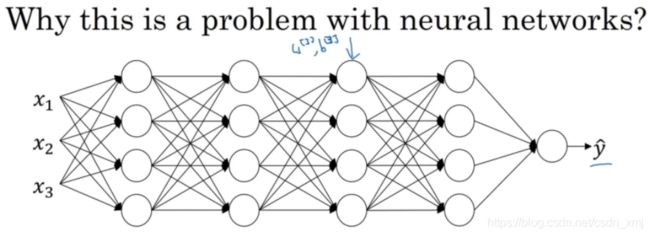
协变量转移是怎么应用于神经网络呢？试想这样一个神经网络：

从第三层来看学习过程。此网络已经学习了参数w^[3]和b^[3]，从前层取得一些值，接下来需要做什么，使输出y帽接近真实值y。

先遮住左边的部分，从第三隐藏层来看，它输入一些值a_1^[2]，a_2^[2]，a_3^[2]，a_4^[2]。第三层隐藏层的工作是找到一种方式，使这些值映射到y帽。（黑色签字笔标注）现在把这个网络的左边揭开：

注意到这个网络的参数还有w^[2]，b^[2]和w^[1]，b^[1]，如果这些参数改变，则a^[2]的值也会改变。所以从第三层隐藏层的角度来看，这些隐藏单元的值在不断地改变，就有了“Covariate shift”的问题，之前讲过的。Batch归一化做的，是它减少了这些隐藏值（hidden unit values）分布变化的数量。它限制了在前层的参数更新，会影响数值分布的程度，第三层看到的这种情况，因此得到学习。

Batch归一化减少了输入值改变的问题（the problem of the input values changing），它的确使这些值变得更稳定（stable），神经网络的之后层就会有更坚实的基础。即使使输入分布改变了一些，它会改变得更少。它做的是当前层保持学习，当改变时，迫使后层适应的程度减小了，你可以这样想，它减弱了前层参数的作用与后层参数的作用之间的联系，它使得网络每层都可以自己学习，稍稍独立于其它层，这有助于加速整个网络的学习。

Batch归一化还有一个作用，它有轻微的正则化效果：

具体表现在：

①每个mini-batch都进行均值为0，方差为1的归一化操作。

②每个mini-batch中，对各个隐藏层的Z^[l]添加了随机噪声，效果类似于Dropout，有轻微的正则化效果。

③mini-batch越小，正则化效果越明显。

但是，不要吧Batch归一化当做正则化，它的正则化效果比较微弱，把它当做归一化隐藏单元激活值并加速学习的方式，Andrew认为正则化几乎是一个意想不到的副作用。

注意一个细节，Batch归一化一次只能处理一个mini-batch数据，它在mini-batch上计算均值和方差。所以测试时，你试图做出预测，试着评估神经网络，你也许没有mini-batch的例子，你也许一次只能进行一个简单的例子，所以测试时，你需要做一些不同的东西以确保你的预测有意义。下一个视频介绍如何让神经网络应用Batch归一化来做出预测。

《3.7 测试时的 Batch Norm》Batch Norm at test time

Batch归一化将你的数据以mini-batch的形式逐一处理，但在测试时，你可能需要对每个样本逐一处理，我们来看一下怎样调整你的网络来做到这一点。

在一个mini-batch中，计算均值和方差，这里用m表示mini-batch中样本数量，而不是整个数据集。注意到μ和σ2是对单个mini-batch中所有m个样本求得的。在测试过程中，如果只有一个样本，求其均值和方差是没有意义的，就需要对μ和σ2进行估计。估计的方法有很多，理论上我们可以将整个训练集放入最终的神经网络模型中，然后将每个隐藏层计算得到的μ^[l]和σ2^[l]直接作为测试过程的μ和σ2来使用。但是，实际应用中一般不使用这种方法，而是使用我们之前介绍过的指数加权平均（exponentially weighted average）的方法来预测测试过程单个样本的μ和σ2。在实践中，不管你用什么方式估算μ和σ2，这套过程都是比较稳健的，因此不担心你具体的操作方式，而且如果你使用的是某种深度学习框架，通常会有默认的估算μ和σ2的方式，应该一样会起到比较好的效果。但在实践中，任何合理的估算你的隐藏单元值的均值和方差的方式，在测试中应该都会有效。

Batch归一化就讲到这里，使用Batch归一化，能够训练更深的网络，让学习算法运行速度更快，在结束这周的课程之前，Andrew还想和你们分享一些关于深度学习框架的想法，让我们在下一段视频中一起讨论这个话题。

《3.8 Softmax 回归》Softmax Regression

到目前为止，我们讲到过的分类的例子都使用了二分分类，这种分类只有两种可能的标记0或1，这是一只猫或者不是一只猫，如果我们有多种可能的类型的话呢？有一种logistic回归的一般形式，叫做Softmax回归（Softmax regression），能让你在试图识别某一分类时做出预测，或者说是多种分类中的一个，不只是识别两个分类，下面来一起看一下。

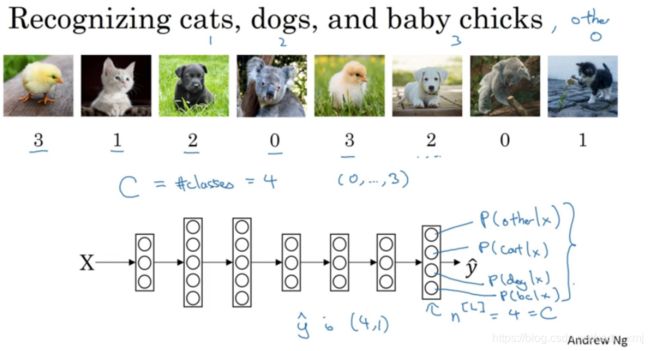
如上图，我们想识别猫（cats），狗（dogs）和小鸡（baby chicks），我把猫加做类1，狗为类2，小鸡是类3，如果不属于以上任何一类，就分到“其它”或者说“以上均不符合”这一类，我把它叫做类0。用大写C来表示类别总个数，这里C=4。我们想要输出层单元的数字告诉我们这4种类型中每个的概率有多大，这里从上到下分别为：其他、猫、狗、小鸡。因此输出y帽是一个4*1维向量，输出必须是数字，而且加起来等于1。

让你的网络做到这一点的标准模型要用到Softmax层，以及输出层来生成输出，式子如下图：

在神经网络的最后一层，和往常一样，计算

算出z之后，应用Softmax激活函数，这个激活函数对于Softmax层而言有些不同，它的作用是这样的。首先，我们要计算一个临时变量（temporary variable），记为t，公式如下：

上式对所有元素求幂，t也是一个4*1维向量，下面计算输出a^[l]：

这里a^[l]也是一个4*1维向量。具体可以看这个例子（上图右）。

总结一下从z^[l]到a^[l]的计算步骤，整个计算过程，从计算幂到得出临时变量，再归一化，我们可以将此概括为一个Softmax激活函数。这一激活函数的与众不同之处在于，需要输入一个4×1维向量，然后输出一个4×1维向量。之前，我们的激活函数都是接受单行数值输入（single row value input），例如Sigmoid和ReLu激活函数，输入一个实数（real number），输出一个实数。Softmax激活函数的特殊之处在于，因为需要将所有可能的输出归一化，就需要输入一个向量，最后输出一个向量。

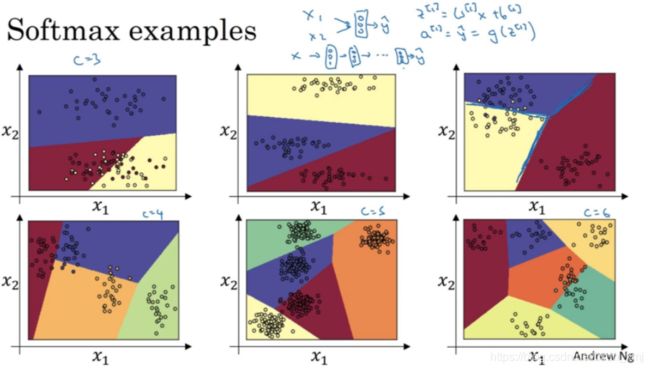
那么Softmax分类器还可以代表其它的什么东西么？假设你有两个输入x1，x2，它们直接输入到Softmax层，它有三四个或者更多的输出节点，输出y帽。下面展示没有隐藏层的神经网络：

输出分类的Softmax层能够代表这种类型的决策边界（decision boundaries），请注意这是几条线性决策边界。

这个视频了解了神经网络中的Softmax层或者Softmax激活函数有什么作用，下一个视频中，我们来看一下你该怎样训练一个使用Softmax层的神经网络。

《3.9 训练一个Softmax分类器》Training a softmax classifier

上一个视频中我们学习了Softmax层（layer）和Softmax激活函数（activation function），在这个视频中，你将更深入地了解Softmax分类（classification），并学习如何训练一个使用了Softmax层的模型。回忆之前的例子：

注意到向量z中，最大的元素是5，而最大的概率也就是第一种概率。

Softmax回归或Softmax激活函数将logistic激活函数推广到类，而不仅仅是两类，结果就是如果，那么的Softmax实际上变回了logistic回归。

接下来，我们来看怎样训练带有Softmax输出层的神经网络，具体而言，我们先定义训练神经网络使会用到的损失函数。举个例子，如下图：

训练集中某个样本的真实标签是[0 1 0 0]，上个视频中这表示猫，目标输出y帽=[0.3 0.2 0.1 0.4]，这里只分配20%是猫的概率，所以这个神经网络在本例中表现不佳。那么你想用什么损失函数来训练这个神经网络？在Softmax分类中，我们一般用到的损失函数是：

对上面的样本而言，y1=y3=y4=0，y2=1，于是有：

这就意味着，如果你的学习算法试图将损失函数L变小，因为梯度下降法是用来减少训练集的损失的，要使它变小的唯一方式就是使y2帽尽可能大，因为这些是概率，所以不可能比1大，但这的确也讲得通，因为在这个例子中是猫的图片，你就需要这项输出的概率尽可能地大。

概括来讲，损失函数所做的就是它找到你的训练集中的真实类别，然后试图使该类别相应的概率尽可能地高，如果你熟悉统计学中最大似然估计（maximum likelihood estimation statistics），这其实就是最大似然估计的一种形式。但如果你不知道那是什么意思，也不用担心。

这是单个训练样本的损失，整个训练集的损失又如何呢？也就是设定参数的代价之类的，还有各种形式的偏差的代价，它的定义你大致也能猜到，就是整个训练集损失的总和，把你的训练算法对所有训练样本的预测都加起来：

因此你要做的就是用梯度下降法，使这里的损失最小化。

最后，我们来看一下，在有Softmax输出层时如何实现梯度下降法：

这个输出层会计算z^[l]，它是C*1维的，这个例子中是4*1，然后你用softmax激活函数得到y帽，又能由此计算出损失（loss）。那么反向传播步骤或者梯度下降法又如何呢？其实初始化反向传播所需要的关键步骤或者说关键方程是这个表达式：

你可以用y帽这个4×1向量减去y这个4×1向量，你可以看到这些都会是4×1向量，当你有4个分类时，在一般情况下就是C*1，这符合我们对的一般定义，这是对损失函数的偏导数（partial derivative）。

通常你只需要专注于把前向传播做对，只要你将它指明为编程框架，前向传播，它自己会弄明白怎样反向传播，会帮你实现反向传播，所以上面这个表达式值得牢记。

Softmax分类就讲到这里，有了它，你就可以运用学习算法将输入分成不止两类，而是C个不同类别。接下来我想向你展示一些深度学习编程框架，可以让你在实现深度学习算法时更加高效，让我们在下一个视频中一起讨论。

《3.10 深度学习框架》Deep learning frameworks

我们已经差不多从零开始学习了使用Python和NumPy实现深度学习算法，希望你理解这些深度学习算法实际上在做什么。但你会发现，除非应用更复杂的模型，例如卷积神经网络，或者循环神经网络，或者当你开始应用很大的模型，否则它就越来越不实用了，至少对大多数人而言，从零开始全部靠自己实现并不现实。

幸运的是，现在有很多好的深度学习软件框架（deep learning programming frameworks），可以帮助你实现这些模型。类比一下，假设你知道如何做矩阵乘法，你还应该知道如何编程实现两个矩阵相乘，但是当你在建很大的应用时，你很可能不想用自己的矩阵乘法函数，而是想要访问一个数值线性代数库，它会更高效，但如果你明白两个矩阵相乘是怎么回事还是挺有用的。Andrew认为现在深度学习已经很成熟了，利用一些深度学习框架会更加实用，会使你的工作更加有效，那就让我们来看下有哪些框架。如下图：

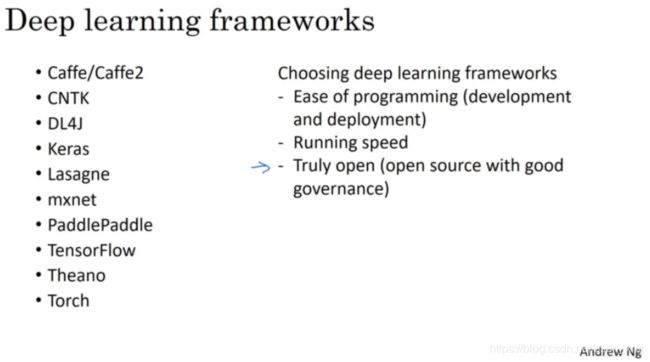
现在有许多深度学习框架，能让实现神经网络变得更简单，我们来讲主要的几个。每个框架都针对某一用户或开发群体的，这里的每一个框架都是某类应用的可靠选择，有很多人写文章比较这些深度学习框架，以及这些深度学习框架发展得有多好，而且因为这些框架往往不断进化，每个月都在进步，如果你想看看关于这些框架的优劣之处的讨论，建议自己去网上搜索，Andrew认为很多框架都在很快进步，越来越好，因此我就不做强烈推荐了，而是与你分享推荐一下选择框架的标准。

①一个重要的标准就是便于编程（Ease of programming），这既包括神经网络的开发和迭代，还包括为产品进行配置，为了成千上百万，甚至上亿用户的实际使用，取决于你想要做什么。

②第二个重要的标准是运行速度（Running speed），特别是训练大数据集时，一些框架能让你更高效地运行和训练神经网络。

还有一个标准人们不常提到，但我觉得很重要，那就是③这个框架是否真的开放（Truly open），要是一个框架真的开放，它不仅需要开源（open source ），而且需要良好的管理（good governance）。不幸的是，在软件行业中，一些公司有开源软件的历史，但是公司保持着对软件的全权控制，当几年时间过去，人们开始使用他们的软件时，一些公司开始逐渐关闭曾经开放的资源，或将功能转移到他们专营的云服务中。因此我会注意的一件事就是你能否相信这个框架能长时间保持开源，而不是在一家公司的控制之下，它未来有可能出于某种原因选择停止开源，即便现在这个软件是以开源的形式发布的。但至少在短期内，取决于你对语言的偏好，看你更喜欢Python，Java还是C++或者其它什么，也取决于你在开发的应用，是计算机视觉，还是自然语言处理或者线上广告，等等，我认为这里的多个框架都是很好的选择。

程序框架就讲到这里，通过提供比数值线性代数库更高程度的抽象化，这里的每一个程序框架都能让你在开发深度机器学习应用时更加高效。

《3.11 TensorFlow》TensorFlow

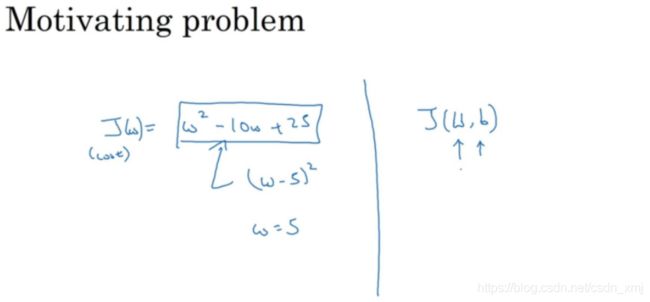
欢迎来到这周的最后一个视频，有很多很棒的深度学习编程框架（deep learning programming frameworks），其中一个是TensorFlow。假设你有一个成本函数J需要最小化：

先自行分析一下，w=5取到最小值：

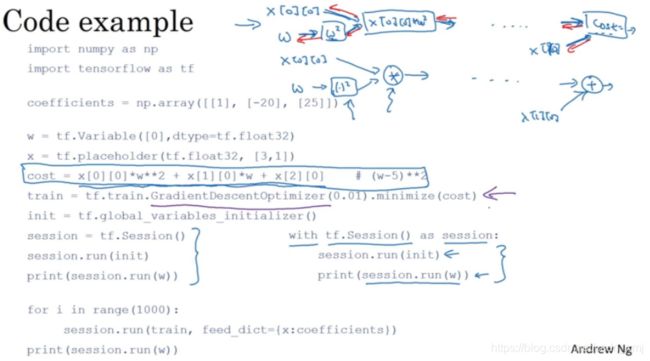
我们来看一下怎样用TensorFlow将其最小化，因为一个非常类似的程序结构可以用来训练神经网络。代码如下：

我在我的Jupyter notebook中运行Python（下面代码可复制，自行操作）：

import numpy as np 
import tensorflow as tf
#导入TensorFlow 
w = tf.Variable(0,dtype = tf.float32) 
#接下来，让我们定义参数w，在TensorFlow中，你要用tf.Variable()来定义参数 
#然后我们定义损失函数： 
cost = tf.add(tf.add(w**2,tf.multiply(- 10.,w)),25) 
#然后我们定义损失函数J #然后我们再写： 
train = tf.train.GradientDescentOptimizer(0.01).minimize(cost) 
#(让我们用0.01的学习率，目标是最小化损失)。 
#最后下面的几行是惯用表达式: 
init = tf.global_variables_initializer() 
session = tf.Sessions()
#这样就开启了一个TensorFlow session。 
session.run(init)
#来初始化全局变量。 
#然后让TensorFlow评估一个变量，我们要用到: session.run(w) 
#上面的这一行将w初始化为0，并定义损失函数，我们定义train为学习算法，它用梯度下降法优化器使损失函数最小化，但实际上我们还没有运行学习算法，所以上面的这一行将w初始化为0，并定义损失函数，我们定义train为学习算法，它用梯度下降法优化器使损失函数最小化，但实际上我们还没有运行学习算法，所以session.run(w)评估了w，让我们打印结果： 
print(session.run(w))

#所以如果我们运行这个，它评估等于0，因为我们什么都还没运行。

#现在让我们输入： 
session.run(train)
#它所做的就是运行一步梯度下降法。 
#接下来在运行了一步梯度下降法后，让我们评估一下w的值，再print： 
print(session.run(w)) 
#0.1 
#在一步梯度下降法之后，w现在是0.1。

#现在我们运行梯度下降1000次迭代：

for i in range(1000):

    session.run(train)

print(session.ran(w)) 

#输出结果：4.99999，与5很接近了。

w是我们想要优化的参数，因此将它称为变量（variable），注意我们需要做的就是定义一个损失函数，使用这些add和multiply之类的函数。TensorFlow知道如何对add和mutiply，还有其它函数求导，这就是为什么你只需基本实现前向传播，它能弄明白如何做反向传播和梯度计算，因为它已经内置在add，multiply和平方函数中。对了，要是觉得这种写法不好看的话，TensorFlow其实还重载了一般的加减运算等等，因此你也可以把写成更好看的形式，把之前的cost标成注释，重新运行，得到了同样的结果。

如果你想要最小化的函数是训练集函数又如何呢？不管你有什么训练数据，当你训练神经网络时，训练数据会改变，那么如何把训练数据加入TensorFlow程序呢？操作如下：

希望你了解了TensorFlow能做什么，让它如此强大的是，你只需说明如何计算损失函数，它就能求导，而且用一两行代码就能运用梯度优化器，Adam优化器或者其他优化器。

#具体代码讲解：

#可以定义x，把它想做扮演训练数据的角色，事实上训练数据有x和y，但这个例子中只有x，把定义为：

x = tf.placeholder(tf.float32,[3,1])

#让它成为[3,1]数组，因为这个二次方程的三项前有固定的系数，我们可以把这些数字1，-10和25变成数据，我要做的就是把cost替换成：

cost = x[0][0]*w**2 +x[1][0]*w + x[2][0]

#现在x变成了控制这个二次函数系数的数据，这个placeholder函数告诉TensorFlow，你稍后会为x提供数值。

#让我们再定义一个数组（array），

coefficient = np.array([[1.],[-10.],[25.]])

#这就是我们要接入x的数据。最后我们需要用某种方式把这个系数数组接入变量x，做到这一点的句法是，在训练这一步中，要提供给x的数值，在这里设置：

feed_dict = {x:coefficients}

#重新运行，得到之前一样的结果。

还是刚才的代码，整理一下得到：

注意到with结构也会在很多TensorFlow程序中用到，它的意思基本上和左边的相同，但是Python中的with命令更方便清理，以防在执行这个内循环时出现错误或例外。

TensorFlow的优点在于建立了计算图（computation graph），通过用这个计算损失，计算图基本实现前向传播，TensorFlow已经内置了所有必要的反向函数，回忆一下训练深度神经网络时的一组前向函数和一组反向函数，而像TensorFlow之类的编程框架已经内置了必要的反向函数，这也是为什么通过内置函数来计算前向函数，它也能自动用反向函数来实现反向传播，即便函数非常复杂，再帮你计算导数，这就是为什么你不需要明确实现反向传播，这是编程框架能帮你变得高效的原因之一。感兴趣的朋友可以关注更详细的TensorFlow相关文档。

Summary

概括一下这周的内容，我们学习了如何系统化地组织超参数搜索过程，我们还讲了Batch归一化，以及如何用它来加速神经网络的训练，最后我们讲了深度学习的编程框架，有很多很棒的编程框架，这最后一个视频我们重点讲了TensorFlow（如果感兴趣，可以查看相关文档）。

说明：记录学习笔记，如果错误欢迎指正！转载请联系我。