Spectral Normalization谱归一化的理解

前置知识之—— 利普希茨连续（Lipschitz continuous）

Lipschitz连续，要求函数图像的曲线上任意两点连线的斜率一致有界，就是任意的斜率都小于同一个常数，这个常数就是Lipschitz常数。

从局部看：我们可以取两个充分接近的点，如果这个时候斜率的极限存在的话，这个斜率的极限就是这个点的导数。也就是说函数可导，又是Lipschitz连续，那么导数有界。反过来，如果可导函数，导数有界，可以推出函数Lipschitz连续。
从整体看：Lipschitz连续要求函数在无限的区间上不能有超过线性的增长，所以这些和函数在无限区间上不是Lipschitz连续的。
记下式为L-Lipschitz.

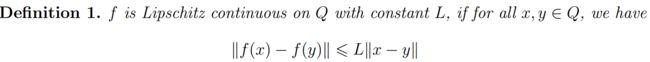
L2归一化

Spectral Normalization

直观地来说，Lipschitz 条件限制了函数变化的剧烈程度，即函数的梯度。在一维空间中，很容易看出 y=sin(x) 是 1-Lipschitz 的，它的最大斜率是 1。

得到谱范数 σ_l(W)后，每个参数矩阵上的参数皆除以它，以达到归一化的目的。

Python实现

import torch
from torch.optim.optimizer import Optimizer, required

from torch.autograd import Variable
import torch.nn.functional as F
from torch import nn
from torch import Tensor
from torch.nn import Parameter

def l2normalize(v, eps=1e-12):
    return v / (v.norm() + eps)


class SpectralNorm(nn.Module):
    def __init__(self, module, name='weight', power_iterations=1):
        super(SpectralNorm, self).__init__()
        self.module = module
        self.name = name
        self.power_iterations = power_iterations
        if not self._made_params():
            self._make_params()

    def _update_u_v(self):
        u = getattr(self.module, self.name + "_u")
        v = getattr(self.module, self.name + "_v")
        w = getattr(self.module, self.name + "_bar")

        height = w.data.shape[0]
        for _ in range(self.power_iterations):
            v.data = l2normalize(torch.mv(torch.t(w.view(height,-1).data), u.data))
            u.data = l2normalize(torch.mv(w.view(height,-1).data, v.data))

        # sigma = torch.dot(u.data, torch.mv(w.view(height,-1).data, v.data))
        sigma = u.dot(w.view(height, -1).mv(v))
        setattr(self.module, self.name, w / sigma.expand_as(w))

    def _made_params(self):
        try:
            u = getattr(self.module, self.name + "_u")
            v = getattr(self.module, self.name + "_v")
            w = getattr(self.module, self.name + "_bar")
            return True
        except AttributeError:
            return False


    def _make_params(self):
        w = getattr(self.module, self.name)

        height = w.data.shape[0]
        width = w.view(height, -1).data.shape[1]

        u = Parameter(w.data.new(height).normal_(0, 1), requires_grad=False)
        v = Parameter(w.data.new(width).normal_(0, 1), requires_grad=False)
        u.data = l2normalize(u.data)
        v.data = l2normalize(v.data)
        w_bar = Parameter(w.data)

        del self.module._parameters[self.name]

        self.module.register_parameter(self.name + "_u", u)
        self.module.register_parameter(self.name + "_v", v)
        self.module.register_parameter(self.name + "_bar", w_bar)


    def forward(self, *args):
        self._update_u_v()
        return self.module.forward(*args)

参考链接：
https://blog.csdn.net/Rocky6688/article/details/103997691
https://blog.csdn.net/ChaoFeiLi/article/details/110072841