Transformer学习及代码实现 (Attention is all you need论文阅读)

写在前面

该文章的写作主要是为了帮助自己更好地理解, 也由于最近这段时间貌似需要学习不少Transformer的变种, 所以也就有了这篇文章, 如果有什么问题还请指正. 本文章的写作主要参考了以下资料:

• 论文地址
• Transformer论文逐段精读(by 李沐)
• The Annotated Transformer

由于自己对深度学习的一些模型的结构没有非常深刻的见解, 对整个Paper的Motivation不做过多的介绍, 仅仅简要介绍原论文在Introduction部分提到的两点(主要针对RNN系列的结构):

• 无法并行(RNN结构的信息的传递有先后之分, 所以其结构也无法并行)
• 信息难以保存(同样源自于RNN的结构问题, 在反向传播中, 信息很容易由于序列过长而丢失)

作者们基于以上两点提出了Transformer架构(正如沐神所评论的, 整个文章的结构比较简单, 就是发现问题-解决问题的步骤), 以下将对Transformer的结构进行介绍.

避雷!!!本文中英文夹杂

整体架构

模型的整体架构仍然采用Encoder-Decoder结构, 其整体的结构如下图所示

这个图可以比较清晰的看到Transformer整个的模型架构, 也就是文章中所说的Encoder将$(x_1,\dots ,x_n)$作为输入, 映射到一个连续空间$\mathbf{z}=(z_1,\dots ,z_n)$, Decoder再根据$\mathbf{z}$将其映射到最终的output probability部分. 每一步都是一个自回归. 所以根据以上内容我们可以得到一个编码器解码器的架构, 简单来说可以通过forward()这部分的设计看出Encoder-Decoder架构的设计.

该部分不涉及到一些具体的细节, 但是对于其中一些影响理解的部分, 例如Encoder和Decoder中有设计掩码, 这在后续attention中会涉及到.

class EncoderDecoder(nn.Module):
    """
    A standard Encoder-Decoder architecture. Base for this and many
    other models.
    """

    def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
        super(EncoderDecoder, self).__init__()
        self.encoder = encoder
        self.decoder = decoder
        self.src_embed = src_embed
        self.tgt_embed = tgt_embed
        self.generator = generator

    def forward(self, src, tgt, src_mask, tgt_mask):
        "Take in and process masked src and target sequences."
        return self.decode(self.encode(src, src_mask), src_mask, tgt, tgt_mask)

    def encode(self, src, src_mask):
        return self.encoder(self.src_embed(src), src_mask)

    def decode(self, memory, src_mask, tgt, tgt_mask):
        return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)

以及得到一个Generator结构, 主要是完成上述模型图的最后的output probability部分内容, log_softmax等价于log(softmax(x)), 此处主要是为了使其数值稳定以便后续计算梯度.

class Generator(nn.Module):
    "Define standard linear + softmax generation step."

    def __init__(self, d_model, vocab):
        super(Generator, self).__init__()
        self.proj = nn.Linear(d_model, vocab)

    def forward(self, x):
        return log_softmax(self.proj(x), dim=-1)

Encoder与Decoder的结构设计

在模型结构图中, 可以看到其中有N个相同的Encoder与Decoder的结构(这里能够有N个相同的主要原因是embedding之后的每个词汇的dimension为512, Encoder Decoder输出也为512, 所以此处可以连接起来).

所以该部分代码的主要结构为Attention等结构组成一个Encoder/Decoder Layer, 有N个Layer组成Encoder/Decoder, 所以以下为代码的组织:

Encoder

def clones(module, N):
    "Produce N identical layers."
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])

所以我们可以使用clones函数对Encoder类进行构造

class Encoder(nn.Module):
    "Core encoder is a stack of N layers"

    def __init__(self, layer, N):
        super(Encoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)

    def forward(self, x, mask):
        "Pass the input (and mask) through each layer in turn."
        for layer in self.layers:
            x = layer(x, mask)
        return self.norm(x)

Layer Norm

考虑一个比较简单的情况, 用二维对该方法进行考虑.

• batchNorm在 feature 中进行normalization
• layerNorm则是在 batch上进行normalization
  
  其主要实现如下

class LayerNorm(nn.Module):
    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2

Encoder Layer的主要结构

主要包含两个部分, 如主干图形部分对其进行实现即可, 第一个部分是残差连接的部分, 第二个部分就是Encoder Layer, 但是此处需要注意, 该部分仍然是抽象的实现, 不涉及一个具体的模块儿的实现.

class SublayerConnection(nn.Module):
    """
    A **residual connection** followed by a layer norm.
    Note for code simplicity the norm is first as opposed to last.
    """

    def __init__(self, size, dropout):
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        "Apply residual connection to any sublayer with the same size."
        return x + self.dropout(sublayer(self.norm(x)))

此处涉及attention(见NOTE处, 暂且按下不表, 到Attention处自然明白)

class EncoderLayer(nn.Module):
    "Encoder is made up of self-attn and feed forward (defined below)"

    def __init__(self, size, self_attn, feed_forward, dropout):
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 2)
        self.size = size

    def forward(self, x, mask):
    	# NOTE: 由于是self attention, 所以 q k v三者在Encoder部分相同
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
        return self.sublayer[1](x, self.feed_forward)

Decoder与Decoder Layer

其设计逻辑仍然和Encoder类似:

class Decoder(nn.Module):
    "Generic N layer decoder with masking."

    def __init__(self, layer, N):
        super(Decoder, self).__init__()
        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)

    def forward(self, x, memory, src_mask, tgt_mask):
        for layer in self.layers:
            x = layer(x, memory, src_mask, tgt_mask)
        return self.norm(x)

只是在第2个Attention的部分有其他输入(参见总模型图)

class DecoderLayer(nn.Module):
    "Decoder is made of self-attn, src-attn, and feed forward (defined below)"

    def __init__(self, size, self_attn, src_attn, feed_forward, dropout):
        super(DecoderLayer, self).__init__()
        self.size = size
        self.self_attn = self_attn
        self.src_attn = src_attn
        self.feed_forward = feed_forward
        self.sublayer = clones(SublayerConnection(size, dropout), 3)

    def forward(self, x, memory, src_mask, tgt_mask):
        "Follow Figure 1 (right) for connections."
        m = memory
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, tgt_mask))
        x = self.sublayer[1](x, lambda x: self.src_attn(x, m, m, src_mask))
        return self.sublayer[2](x, self.feed_forward)

我们还修改了Decoder中的Self-attention层, 以防止位置出现在后续位置上, 这种屏蔽, 输出嵌入偏移了一个位置(即模型图中的shift right)，确保对位置$i$的预测只取决于小于$i$的位置的已知输出.

def subsequent_mask(size):
    attn_shape = (1, size, size)
    subsequent_mask = torch.triu(torch.ones(attn_shape), diagonal=1).type(
        torch.uint8
    )
    return subsequent_mask == 0

Attention

Scaled Dot Product Attention

此处的Attention的计算公式如下所示(主要是需要注意一下对其进行scale的motivation, 为了防止其在softmax中出现梯度消失的问题)

• 补充: $d_k$不大时, 是否除以这个$d_k$都还好, 当$d_k$较大时, 点积值比较极端, 最后就导致了softmax出现老毛病, 此处的dimension比较大, 所以使用了这个trick…(此时使用$d_k$的notation主要是为了遵从原文, 其实就是query的dimension, 由于原文做了multihead的工作所以此时的query的dimension并非是$d_{model}$, ps: 当时光看这里其实还是有点懵的, 后面读到就明白这个啥意思了)

$$\text{Attention}(\mathbf{Q},\mathbf{K},\mathbf{V})=\text{softmax}(\frac{\mathbf{Q}{\mathbf{K}}^{\top }}{\sqrt{d_k}})\mathbf{V}$$

以下是代码, 前面说到了我们要有一个mask的操作, 其中mask的操作其实是填0的, 而在softmax中想要后面的值对其不起作用, 就要使其输出值为0, 而输入的score就要负无穷大.(此处注意其trick)

def attention(query, key, value, mask=None, dropout=None):
    "Compute 'Scaled Dot Product Attention'"
    d_k = query.size(-1)
    # NOTE: 此处的transpose用的是-2和-1, 是和multihead的设计有关
    scores = torch.matmul(query, key.transpose(-2, -1)) / math.sqrt(d_k)
    if mask is not None:
        scores = scores.masked_fill(mask == 0, -1e9)
    p_attn = scores.softmax(dim=-1)
    if dropout is not None:
        p_attn = dropout(p_attn)
    return torch.matmul(p_attn, value), p_attn

MultiHead Attention

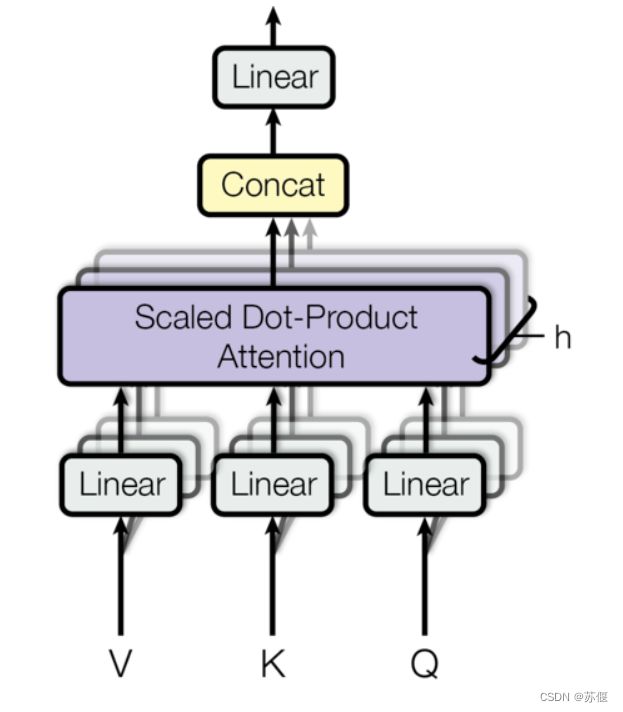
首先看这个结构图

简单来说其主要有两次映射, 第一次映射有多个头, 每个头都能够做一次不同的Linear Transformation(此处不同的Linear transformation代表了不同的这个head去target不同问题的识别), 这些线性层的参数都是需要学习的, 再把$h$次的信息concat起来, 最后做一次Linear Transformation整合多头信息.

具体公式如下所示:

$$\begin{array}{rl}\text{MultiHead}(\mathbf{Q},\mathbf{K},\mathbf{V})& =[{\text{head}}_1;\dots ;{\text{head}}_h]{\mathbf{W}}^O\\ {\text{where head}}_i& =\text{Attention}(\mathbf{Q}{\mathbf{W}}_i^Q,\mathbf{K}{\mathbf{W}}_i^K,\mathbf{V}{\mathbf{W}}_i^V)\end{array}$$

其中${\mathbf{W}}_i^K,{\mathbf{W}}_i^Q,{\mathbf{W}}_i^V,{\mathbf{W}}^O$都是可以学习的参数. 前面三个参数的维度为$d_{model}\times d_k$, 最后一个参数的维度为$h{d}_v\times d_{model}$. 在本文中h为8, 为了保证输入输出一致所以$d_k,d_v$的大小相等, 且均为$d_{model}/h=64$. 其中文章中提到"Due to the reduced dimension of each head, the total computational cost is similar to that of single-head attention with full dimensionality", 可以结合NOTE中的部分, 与该部分公式dimension的变化进行理解, 就发现学习的参数并无变化.

ps:(这段不看也没关系)其与Self Attention的区分点在于多个head, 也就做了多次Attention, 并不在于Linear Transformation的部分, 如果做了Linear Transformation, 而没有分多个head(也就是NOTE代码中的view部分), 那么最终也不会有multihead的效果: target不同问题的识别

class MultiHeadedAttention(nn.Module):
    def __init__(self, h, d_model, dropout=0.1):
        super(MultiHeadedAttention, self).__init__()
        
        assert d_model % h == 0
        # d_k与d_v相等
        self.d_k = d_model // h
        self.h = h
        self.linears = clones(nn.Linear(d_model, d_model), 4)
        self.attn = None
        self.dropout = nn.Dropout(p=dropout)

    def forward(self, query, key, value, mask=None):
        if mask is not None:
            # Same mask applied to all h heads.
            mask = mask.unsqueeze(1)
        nbatches = query.size(0)

        # 1) Do all the linear projections in batch from d_model => h x d_k
        # NOTE: 此处的的query, key, value, 实际上是h个query, key, value进行Linear Projection之后再更改形状, 此时的参数和Full Dimension的是类似的, 此时可以将他们直接放进attn中是因为上述attention的设计得到的
        query, key, value = [
            lin(x).view(nbatches, -1, self.h, self.d_k).transpose(1, 2)
            for lin, x in zip(self.linears, (query, key, value))
        ]

        # 2) Apply attention on all the projected vectors in batch.
        x, self.attn = attention(
            query, key, value, mask=mask, dropout=self.dropout
        )

        # 3) "Concat" using a view and apply a final linear.
        x = (
            x.transpose(1, 2)
            .contiguous()
            .view(nbatches, -1, self.h * self.d_k)
        )
        del query
        del key
        del value
        return self.linears[-1](x)

Position-wise Feed-Forward Networks

感觉该部分比较简单, 直接根据公式往上套即可(代码实际实现增加了正则化部分, 这在文章后面有提到):

class PositionwiseFeedForward(nn.Module):
	# d_ff = 2048
    def __init__(self, d_model, d_ff, dropout=0.1):
        super(PositionwiseFeedForward, self).__init__()
        self.w_1 = nn.Linear(d_model, d_ff)
        self.w_2 = nn.Linear(d_ff, d_model)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        return self.w_2(self.dropout(self.w_1(x).relu()))

Embedding and Softmax

与普通的embedding不同的是, 此处增加了一个$\times {\sqrt{d}}_{model}$的部分, 主要是为了和后面所提到的Postional Encoding在一个scale上面以方便相加. (nn.Embedding可以参考torch文档, 和线性层有不同的地方)

class Embeddings(nn.Module):
    def __init__(self, d_model, vocab):
        super(Embeddings, self).__init__()
        self.lut = nn.Embedding(vocab, d_model)
        self.d_model = d_model

    def forward(self, x):
        return self.lut(x) * math.sqrt(self.d_model)

Position Encoding

由于该模型不包含类似RNN与Conv的结构, 为了使模型能够利用序列的顺序, 需要加入一些关于序列中标记的相对或绝对位置的信息. 为此, 在Encoder与Decoder的底部为输入嵌入添加 “位置编码”. 位置编码$d_{\text{model}}$也具有相同的dimension.

class PositionalEncoding(nn.Module):
    "Implement the PE function."

    def __init__(self, d_model, dropout, max_len=5000):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(p=dropout)

        # Compute the positional encodings once in log space.
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len).unsqueeze(1)
        div_term = torch.exp(
            torch.arange(0, d_model, 2) * -(math.log(10000.0) / d_model)
        )
        pe[:, 0::2] = torch.sin(position * div_term)
        pe[:, 1::2] = torch.cos(position * div_term)
        pe = pe.unsqueeze(0)
        self.register_buffer("pe", pe)

    def forward(self, x):
        x = x + self.pe[:, : x.size(1)].requires_grad_(False)
        return self.dropout(x)

最终

def make_model(
    src_vocab, tgt_vocab, N=6, d_model=512, d_ff=2048, h=8, dropout=0.1
):
    "Helper: Construct a model from hyperparameters."
    c = copy.deepcopy
    attn = MultiHeadedAttention(h, d_model)
    ff = PositionwiseFeedForward(d_model, d_ff, dropout)
    position = PositionalEncoding(d_model, dropout)
    model = EncoderDecoder(
        Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
        Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
        nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
        nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
        Generator(d_model, tgt_vocab),
    )

    # Initialize parameters with Glorot / fan_avg.
    for p in model.parameters():
        if p.dim() > 1:
            nn.init.xavier_uniform_(p)
    return model

其他关于Attention的直觉理解

此处并不强调Attention的字面上的意义. 主要想记录Encoder 和 Decoder中间的连接部分:

• key, value来自Encoder
• query来自Decoder
• key和query其实是决定了权重, value决定最后的输出.
  • 也就是通过query和key的相似度去match Encoder的value最终决定输出.
  • 可以参考沐神的视频有一个你好世界的翻译例子(有时间会把这个例子补充一下)

以上可以引出Attention的直觉的例子, 使用Attention可以通过这种相似度的形式得到两段seq之间应该如何match. 同时Attention有一个"全局观", 假设更少(此处个人是这样理解, Attention只是使用更fancy的方式, 设计了各种更强, 简洁的模式去挖掘文本信息, 例如相对于一条seq, Attention用上的trick就是这么多, 而且把时序信息输入到模型中, 而非像RNN做假设), 适合训练大模型(此处未展开).

下一步学习

希望看看Transformer在其他地方的应用(多模态), 例如ViT以及在Audio上面的Application.