蒙特卡洛方法计算圆周率

import random
import math


def calpai():
    n = 10000000 #随机实验次数
    r = 1.0   #圆的半径
    a, b = (0.0, 0.0)  #中心点
    x_neg, x_pos = a - r, a + r   #x坐标取值范围
    y_neg, y_pos = b - r, b + r   #y坐标取值范围

    count = 0  #落在圆内的概率
    for i in range(0, n):
        x = random.uniform(x_neg, x_pos)
        y = random.uniform(y_neg, y_pos)
        if x*x + y*y <= 1.0:
            count += 1

    return (count / float(n)) * 4

    #print (count / float(n)) * 4

if __name__ == '__main__':
    value = calpai()
    print ("pi = " ,value)
    print ("error = " ,100*abs(math.pi-value)/math.pi,"%")

第一个例子是，如何用蒙特卡罗方法计算圆周率π。

正方形内部有一个相切的圆，它们的面积之比是π/4。

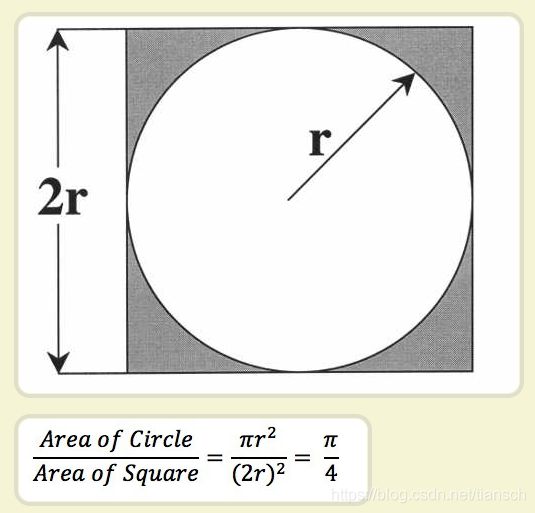
现在，在这个正方形内部，随机产生10000个点（即10000个坐标对 (x, y)），计算它们与中心点的距离，从而判断是否落在圆的内部。

如果这些点均匀分布，那么圆内的点应该占到所有点的 π/4，因此将这个比值乘以4，就是π的值。

参考链接：
http://www.ruanyifeng.com/blog/2015/07/monte-carlo-method.html