Opencv学习笔记(三)线性及非线性滤波
大纲
1.滤波综述
2. 方框滤波
3. 均值滤波
4. 高斯滤波
5. 中值滤波
6. 双边滤波
一、滤波综述
图像的滤波指的是在尽量保证图像细节特征的的情况下对图像中的噪声进行抑制,又因为图像的能量大部分集中在低频或者中频的区域(图像大部分区域是连贯的,波动不大,频率),而高频部分则大多为边缘信息(图像变换快)或者是噪声。所以滤波器分为两种,低通滤波和高通滤波,前者的作用就是保证低频区域的稳定,尽量去除噪声,但也不可避免的带来边缘信息的丧失,所以也称作“平滑”或者“模糊”;后者则着重于增强图像的边缘信息,对于噪声的抑制则较弱,所以也叫做“锐化”。本次要介绍的几个滤波器都是着重于抑制图像的噪声,可以算是低通滤波器,且都为邻域算子滤波即通过卷积核和源图像卷积,给定像素周围像素值决定此像素最终值。
二、方框滤波与均值滤波
方框滤波是将一个全为1的卷积核与源图像进行卷积,像素加权得到,而均值滤波则是在此基础进行了归一化,规避了溢出的风险。这中方法是用待求像素周围矩形区域像素的均值来代替该值(这样点上教材上是说待求点本身不介入均值运算,但网上各类代码及卷积核介绍都是将待求点也介入,倾向于后者正确),因为典型的噪声就是灰度值的急剧变化,而图像区域一般是连续的,通过这样方式就可以平滑噪声,但同时也造成了边缘信息的丧失。卷积核如下:
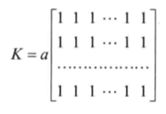
当a为1时,就是方框滤波;当a=元素数目时,就是均值滤波。
opencv中方框滤波函数原型如下:
boxFilter( InputArray src, OutputArray dst, int ddepth,Size ksize, Point anchor = Point(-1,-1),bool normalize = true,int borderType = BORDER_DEFAULT );
第一个参数为输入图像,通道数不限,滤波函数对通道都是单独处理的,但深度需要为CV_8U,CV_16U,CV_16S,CV_32F,CV_64F之一;
第二个参数为输出图像,需要和输入图像同类型同大小;
第三个参数为输出图像的深度,选填-1则为保持原深度,当输出结果可能溢出时换用其他值;
第四个参数为卷积核的大小,Size类型,一般选用奇数长正方形区域;
第五个参数为锚点,即被平滑的点(均值代替的点),默认值(-1,-1)表示为卷积核中心;
第六个参数为归一化选项,如果选1则变成了均值滤波;
第七个参数为边缘填充选项,有默认值BORDER_DEFAULT;
均值滤波函数原型:
blur( InputArray src, OutputArray dst,Size ksize, Point anchor = Point(-1,-1),int borderType = BORDER_DEFAULT );
参数介绍与方框滤波一致。
二、高斯滤波
高斯滤波也是通过卷积核与原图像卷积,像素加权得到,但与均值滤波不同的是卷积区域内像素的权值不再相同,而是满足二维正态(高斯)分布,离中心越近权值越大,离中心越远权值越小,这样可以有效抑制服从正态分布的噪声。二维高斯分布数学公式如下:
f ( x , y ) = 1 2 π ( σ x 2 + σ y 2 ) e − ( x − μ x ) 2 2 σ x 2 − ( y − μ y ) 2 2 σ y 2 f(x,y)=\frac{1}{\sqrt{2\pi(\sigma_x^2+\sigma_y^2)}}e^{-\frac{(x-\mu_x)^2}{2\sigma_x^2}-\frac{(y-\mu_y)^2}{2\sigma_y^2}} f(x,y)=2π(σx2+σy2)1e−2σx2(x−μx)2−2σy2(y−μy)2
因为后续要进行归一化所以前面的系数也不重要; μ x 、 μ y \mu_x、\mu_y μx、μy均为卷积中心,最终我们用到的公式为:
f ( x , y ) = A e − ( x − μ x ) 2 2 σ x 2 − ( y − μ y ) 2 2 σ y 2 f(x,y)=Ae^{-\frac{(x-\mu_x)^2}{2\sigma_x^2}-\frac{(y-\mu_y)^2}{2\sigma_y^2}} f(x,y)=Ae−2σx2(x−μx)2−2σy2(y−μy)2
通过这个公式计算出相应大小的卷积核之后再进行归一化,如设置 σ = 1.5 \sigma=1.5 σ=1.5后计算3×3卷积核为:
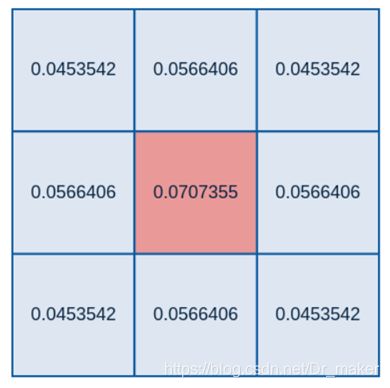
归一化之后:

高斯滤波函数原型为:
GaussianBlur( InputArray src, OutputArray dst, Size ksize,double sigmaX, double sigmaY = 0,int borderType = BORDER_DEFAULT );
前两个参数为输入、输出图像;
第三个参数为卷积核大小,长度宽度可以不同,但必须都是正奇数,如果都设为0的话将由后续sigma计算出来,计算方法可参见参考文献。
第四、五个参数为X,Y方向上的标准偏差,通常是不分辨X,Y方向上的区别,两个取值相同;当sigmaY=0时,sigmaY=sigmaX;当sigmaY=sigmax=0时,他们的值由卷积核大小代入下述公式确定:
σ = 0.3 × ( ( k s i z e − 1 ) × 0.5 − 1 ) + 0.8 \sigma = 0.3\times((ksize - 1)\times0.5 - 1) + 0.8 σ=0.3×((ksize−1)×0.5−1)+0.8
第六个参数为边界填充类型
五、中值滤波
中值滤波三种滤波不同,为非线性滤波,虽然也是通过窗函数在原图上滑动得到每一个待求像素的值,但该值并不再是窗函数范围内像素的加权和了,而是像素排序之后的中位数。与均值滤波相比,它几乎不会受到噪声尤其是椒盐噪声的影响,因为这种极值很难被选为中位数,由此中值滤波的去噪效果比均值滤波要更好,同时由于矩形窗范围内存在的边缘也应该是连续的,保存边缘的效果也更好,但它也有缺点:计算时间过长,是均值滤波的5倍以上(未验证)。
opencv函数原型:
medianBlur( InputArray src, OutputArray dst, int ksize );
第一、二个参数为输入输出图像;
第三个参数为窗函数的线性尺寸,应该为正奇数,即3×3,5×5这样的方形窗。
六、双边滤波
双边滤波同样是非线性滤波,从某种意义上来说它与高斯滤波很相似,高斯滤波考虑了距离对于权重的影响,双边滤波再次基础之上考虑了像素相似程度对与权重的影响,从而在边缘附近,离得较近的点由于像素值相差过大权重小,离得较远的点距离过大权重小,从而可以较好的保留边缘信息,但也因此不能很好的滤去高频信息。数学公式如下:
g ( i , j ) = ∑ k , l f ( k , l ) ω ( i , j , k , l ) ∑ k , l ω ( i , j , k , l ) g(i,j)= {{\sum_{k,l}f(k,l)\omega(i,j,k,l)}\over{\sum_{k,l}\omega(i,j,k,l)}} g(i,j)=∑k,lω(i,j,k,l)∑k,lf(k,l)ω(i,j,k,l)
其中 f ( k , l ) f(k,l) f(k,l)为原像素值, w ( i , j , k , l ) w(i,j,k,l) w(i,j,k,l)为加权值取决于空间域核和色彩域核的乘积
空间域核:
d ( i , j , k , l ) = e − ( i − k ) 2 + ( j − l ) 2 2 σ d 2 d(i,j,k,l)=e^{-\frac{(i-k)^2+(j-l)^2}{2\sigma_d^2}} d(i,j,k,l)=e−2σd2(i−k)2+(j−l)2
色彩域核:
r ( i , j , k , l ) = e − ∣ ∣ f ( i , j ) − f ( k , l ) ∣ ∣ 2 2 σ r 2 r(i,j,k,l)=e^{-\frac{||f(i,j)-f(k,l)||^2}{2\sigma_r^2}} r(i,j,k,l)=e−2σr2∣∣f(i,j)−f(k,l)∣∣2
权重:
w ( i , j , k , l ) = e − ( i − k ) 2 + ( j − l ) 2 2 σ d 2 − ∣ ∣ f ( i , j ) − f ( k , l ) ∣ ∣ 2 2 σ r 2 w(i,j,k,l)=e^{-\frac{(i-k)^2+(j-l)^2}{2\sigma_d^2}-\frac{||f(i,j)-f(k,l)||^2}{2\sigma_r^2}} w(i,j,k,l)=e−2σd2(i−k)2+(j−l)2−2σr2∣∣f(i,j)−f(k,l)∣∣2
opencv函数原型如下:
bilateralFilter( InputArray src, OutputArray dst, int d,double sigmaColor, double sigmaSpace,int borderType = BORDER_DEFAULT );
第一、二个参数为输出输出图像;
第三个参数为像素邻域的直径,如果这个值被设为负数,则由sigmaspace计算得出;
第四个参数为公式中的 σ r \sigma_r σr,这个值越大,表明越宽广的颜色会被混合到一起,即对颜色的区分下降;
第五个参数为公式中的 σ d \sigma_d σd,这个值越大,表明越远距离的值会介入运算,对距离的区分下降,当d大于0它确定了邻域大小且与此参数无关,否则d正比于此参数;
第六个参数为边界填充方式;
参考文献
双边滤波算法介绍与实现
中值滤波介绍与实现
高斯滤波介绍与实现
均值滤波介绍与实现
如何确定高斯滤波标准差和窗口大小