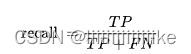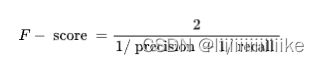深度学习算法面试常问问题（二）

X86和ARM架构在深度学习侧的区别？

X86和ARM架构分别应用于PC端和低功耗嵌入式设备，X86指令集很复杂，一条很长的指令就可以完成很多功能；而ARM指令集很精简，需要几条精简的短指令完成很多功能。

影响模型推理速度的因素？

• FLOPs（模型总的乘加运算）
• MAC（内存访问成本）
• 并行度（模型推理时操作的并行度越高，速度越快）
• 推理平台

减少模型内存占用有哪些方法？

• 模型剪枝
• 模型蒸馏
• 模型量化
• 模型结构调整

图像阈值法

• 全局阈值：对整个图像中的每一个像素都选用相同的阈值。
• 局部阈值：又称自适应阈值，局部阈值法假定图像在一定区域内受到的光照比较接近。它用一个滑窗扫描图像，并取滑窗中心点亮度与滑窗其他区域的亮度进行比较，如果中心点亮度高于邻域亮度，则将中心点设为白色，否则设为黑色。

图像膨胀腐蚀的相关概念

图像的膨胀和腐蚀是两种基本的形态学运算，主要用来寻找图像中的极大区域和极小区域。

• 膨胀：将图像的高亮区域或白色部分进行扩张，其运行结果比原图的高亮区域更大
• 腐蚀：反之亦然

边缘检测

图像边缘是图像最基本的特征，指图像局部特征的不连续性。图像边缘有方向和幅度两种属性。边缘通常可以通过一阶导数和二阶导数检测得到。、

一阶导数：以最大值作为对应的边缘位置，常用的算子：roberts算子，sobel算子和prewitt算子。

二阶导数：以过零点作为对应边缘的位置，常用的算子：laplacian算子，此类算子对噪声敏感。

区别：一阶微分算子获得的边界是比较粗略的边界，反映的边界信息较少（边界很粗），但是所反映的边界比较清晰；二阶微分算子获得的边界是比较细致的边界。反映的边界信息包括了许多的细节信息，但是所反映的边界不是太清晰。

其他边缘算子：前面均是通过微分算子来检测图像边缘，还有一种是canny算子，在满足一定约束条件下推导出来的边缘检测最优化算子。

图像高/低通滤波

高频：图像中灰度变化剧烈的点，一般是图像轮廓或者噪声，常用算子：canny，sobel算子，laplacian算子等边缘算子

低频：图像中平坦的，变化不大的点，也就是图像中大部分区域，常用算子：均值滤波，高斯滤波，中值滤波

均值滤波的缺陷：不能很好地保护图像细节，在图像去噪的同时也破坏了图像的细节部分，从而使图像变模糊，不能很好去除噪音点

高斯滤波的原理和操作步骤：高斯滤波是整幅图像进行加权平均的过程，每一个像素点的值都由本身和领域其他像素点经过加权平均后得到。具体操作是用一个高斯核扫描图像中的每一个像素，用模板确定的邻域内像素的加权灰度值去替代模板中心像素点的值。

中值滤波的原理和使用中值滤波的场景：用像素点邻域灰度值的中值来代替该像素点的灰度值，中值滤波在去除脉冲噪声、椒盐噪声的同时又能保留图像的边缘细节。

常用的色彩空间格式

RGB、RGBA、HSV、HLS、Lab、YCbCr、YUV等

• RGBA是代表Red(红)、Green(绿)、Blue(蓝)和Alpha(透明度)的⾊彩空间
• HSV⾊彩空间（Hue-⾊调、Saturation-饱和度、Value-亮度）将亮度从⾊彩中分解出来，在图像增强算法中⽤途很⼴。
• HLS⾊彩空间，三个分量分别是⾊相(H)、亮度(L)、饱和度(S)。
• Lab⾊彩空间是由CIE(国际照明委员会)制定的⼀种⾊彩模式。⾃然界中任何⼀点⾊都可以在Lab空间中表达出来，它的⾊彩空间⽐RGB空间还要⼤。
• YCbCr进⾏了图像⼦采样，是视频图像和数字图像中常⽤的⾊彩空间。在通⽤的图像压缩算法中（如JPEG算法），⾸要的步骤就是将图像的颜⾊空间转换为YCbCr空间。
• YUV⾊彩空间与RGB编码⽅式(⾊域)不同。RGB使⽤红、绿、蓝三原⾊来表示颜⾊。⽽YUV使⽤亮度、⾊度来表示颜⾊。

Python的GIL

GIL是python的全局解释器锁，同一进程中假如有多个线程运行，一个线程在运行python程序的时候会霸占python解释器（加了一把锁即GIL），使该进程内的其他线程无法运行，等该线程运行完后其他线程才能运行。如果线程运行过程中遇到耗时操作，则解释器锁解开，使其他线程运行。所以在多线程中，线程的运行仍使先后顺序的，并不是同时进行的。GIL存在引起的最直接问题是：在一个解释器进程中通过多线程的方式无法利用多核处理器来实现真正的并行。

多进程中因为每个进程都能被系统分配资源，相当于每个进程都有python解释器，所以多进程可以实现多个进程的同时运行，缺点是进程系统资源开销大。

• python的进程中的线程不能并行，因为GIL，每个线程实际上是交替执行，每次只有一个线程拿到GIL执行程序
• 如果想并行 需要并行进程，而不是并行线程

为什么会有GIL锁？

python是解释型语言，意味着解释一行，运行一行，它并不清楚代码全局；因此每个线程在调用cpython解释器运行之前，需要先抢到GIL锁，然后才能运行；编译型语言就不存在GIL锁，编译型语言会直接编译所有代码。

面对GIL的存在，我们可以有多个方法帮助提升性能

• 在I/O密集型任务下，我们可以使用多线程或者协程来完成
• 可以选择Jython等没有GIL的解释器，但并不推荐更换解释器，因为会错过众多C语言模块中的有用特性
• CPU密集可以使用多进程+进程池

10个linux常用命令

ls pwd cd touch rm mkdir tree cp mv cat more grep echo

python2和python3的区别？列举5个

1. python3 print必须用括号，python2既可以括号， 又可以用空格
2. python3 range返回生成器， python2 返回list
3. python3 使用utf-8编码，python2 使用ascii编码
4. python3中str表示字符串序列， python2中unicode表示字符串序列
5. python3可直接显示中文，python2必须引入coding声明才能正常显示中文
6. python3 input python2 是raw_input()

add和concat操作，有哪些区别与联系呢？

• concat操作而言，通道数的合并，也就是说描述图像本身的特征增加了，而每一特征下的信息是没有增加的。例如UNet等分割网络
• add操作更像信息之间的叠加，这里有一个前提是add前后的语义信息是相似的。例如FPN的网络结构设计。

在backbone不变的情况下，若显存有限，如何增大训练时的batchsize？

1.使用trick， 节省显存

• 使用inplace操作，比如relu激活函数，我们可以设置inplace=True
• 每次循环结束时候，我们可以手动删除loss
• 使用fp16混合精度计算
• 训练过程中的显存占用包括前向与反向所保存的值，所以我们在不需要bp的forward时候，我们可以使用torch.no_grad()
• 使用GAP来替代FC等
• 优化器的使用上，理论上，显存占用sgd

2.从反传角度考虑

在训练的时候，CNN主要开销来自于存储用于计算backward的activation，对于一个长度为N的CNN，需要O(N)的内存。在《Training Deep Nets with Sublinear Memory Cost》，每隔sqrt(N)个node存一个activation，需要的时候再算，这样显存就从O(N)降到O(sqrt(N))，pytorch中torch.utils.checkpoint就是实现这样的功能。

3.使用梯度积累

由于显存受限bs只能设置为4，想要通过梯度累积实现bs等于16，这需要4次迭代，每次迭代的loss除以4。

• 获取loss，在计算当前梯度，不过暂时不清空梯度，在已有梯度加上新梯度。当梯度累加到一定次数之后，使用optimizer.step将累计的梯度来更新一下参数
• 梯度积累的效果是不如真实的bs放大8倍的，因为增大8倍bs的图片，其running_mean和running_var更加准确。

语义分割中的IOU

常常将预测出来的结果分成四个部分：TP、FP、TN、FN。

大块白色斜线标记的是TN（预测中真实的背景部分），红色部分标记的是：TN（预测中被预测为背景，但实际上不是背景的部分），蓝色斜线部分是FP（预测分割为某标签的部分，但是其实并不该标签所属的部分），中间黄色块是TP（预测的某标签部分，符合真值）
$$IOU=\frac{\text{ target }\bigwedge \text{ prediction }}{target\bigcup prediction}$$

def compute_ious(pred, label, classes):
    '''computes iou for one ground truth mask and predicted mask'''
    ious = [] # 记录每一类的iou
    for c in classes:
        label_c = (label == c) # label_c为true/false矩阵
        pred_c = (pred == c)
        intersection = np.logical_and(pred_c, label_c).sum()
        union = np.logical_or(pred_c, label_c).sum()
        if union == 0:
            ious.append(float('nan'))  
        else
            ious.append(intersection / union)
    return np.nanmean(ious) #返回当前图片里所有类的mean iou

标签平滑 label smoothing

思路：在训练时假设标签可能存在错误，避免过分相信训练样本标签。在训练样本上，我们并不能保证所有样本标签都标注正确，如果某个样本的标注是错误的，那么在训练时，该样本就有可能对训练结果产生负面影响。很自然的想法是我们可以告诉模型，标签不一定正确，那么训练出的模型对于少量样本错误就会有“免疫力”，从而拥有更好地泛化性能。

sigmoid 和 softmax函数

sigmoid得到的结果是“分到正确类别的概率和未分到正确类别的概率”，softmax得到的是“分到正确类别的概率和分到错误类别的概率”

sigmoid：对于非互斥的多标签分类任务，且我们需要输出多个类别。如一张图我们需要输出是否是男人，是否戴了眼镜，我们可以采用sigmoid来输出最后的结果。例如：[0.01, 0.02, 0.41, 0.62, 0.3, 0.18, 0.5, 0.42, 0.06, 0.81]，我们通过设置一个概率阈值，比如0.3，如果概率值大于0.3，则判定类别符合，那么该输入样本则会被判定为类别3、4、5、7和8，即一个样本具有多个标签。

softmax为什么要引入指数形式？

如果使用max函数，虽然能完美的进行分类但函数不可微从而无法进行训练，引入以e为底的指数并加权归一化，一方面指数函数使得结果将分类概率拉开了距离，另一方面函数可微。

softmax：当我们的任务是一个互斥的多类别分类任务，网络只能输出一个正确答案，我们可以用softmax函数处理各个原始的输出值
$$y_i=\mathrm{Softmax}(x_i)=\frac{e^{x_i}}{{\sum }_{j=1}^n{e}^{x_j}}$$

import numpy as np
def softmax( f ):
    # 为了防止数值溢出，我们将数值进行下处理
    # f： 输入值
    f -= np.max(f) # f becomes [-666, -333, 0]
    return np.exp(f) / np.sum(np.exp(f))  

机器学习分类指标

• accuracy：指的是正确预测的样本数占总预测样本数的比值，它不考虑预测的样本是正例还是负列，考虑的是全部样本

• precision：指的是正确预测的正样本数占所有预测为正样本的数量比值，precision只关注预测为正样本的部分

• recall：指的是正确预测的正样本数占真实样本总数的比值，也就是我能从这些样本中能够正确找出多少个正样本

• F-score：相当于precision和recall的调和平均。公式中可以看出，recall和precision任何一个数值减少，F-score都会减少。

• P-R曲线：纵轴设置为precision，横轴设置成recall，改变阈值就能获得一系列的pair并绘制曲线，一般来说如果一个曲线完全包围另外一个曲线，我们可以认为该模型的分类效果要好于对比模型。（AP）

• ROC：在实际的数据集中经常出现类别不平衡现象，即负样本比正样本多很多（或相反），而且在测试数据中的正负样本的分布也可能随着时间而变化。而在这种情况下，roc曲线能够保持不变。同时，我们可以断言，roc曲线越接近左上角，该分类器的性能越好，意味着分类器在假阳性很低的同时获得了很高的真阳率。

图像分割指标

• pixel accuracy（标记正确 / 总像素数目），优点：简单。缺点是：图像中大面积是背景，而目标较少，即使整个图片预测为背景也会有很高的PA得分。

• MPA（mean pixel accuracy）:计算每类各自分类的准确率，再取均值。

  

• MIou：计算两个集合的交集与并集之比，在语义分割中，这两个集合为真实值和预测值。

• FWIoU：MIou的一种提升，这种方法可以根据每个类出现的频率为其设置权重。

目标检测指标

• mAP：即各类别AP的平均值
• AP：PR曲线下的面积
• PR曲线：Precision-Recall曲线
• Precision： TP/(TP + FP)
• Recall: TP/(TP+FN)
• TP: IoU > 0.5的检测框数量
• FP：IoU <= 0.5的检测框，或者是检测到同一个GT的多余检测框（NMS）
• FN：没有检测到GT的数量

激活函数

• mish激活函数：

$$\text{ Mish }=x\ast \tanh \left(\ln \left(1+e^x\right)\right)$$

mish函数：理论上对负值的轻微允许更好的梯度流，而不是像ReLU中那样硬边界。其中最重要的是平滑型激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化。pytorch版本的mish比较占显存。

• Leaky Relu与PRelu：前者是设置一个超参数，后者将超参数设置成一个可学习的参数，优点：（1）计算简单有效（2）比sigmoid与tanh收敛更快（3）解决了dead神经元的问题。

• RRelu是leaky relu的一个变体，在RRelu中，斜率是一个给定范围内随机抽取的值，这个值在测试环节就会固定下来。

• swish函数：

$$f(x)=x\cdot \mathrm{sigmoid}(\beta x)$$

• GELU(Gaussian Error Linear Unit)：灵感来源于relu和dropout，在激活中引入随机正则的思想。gelu通过输入自身的概率分布情况，决定抛弃还是保留当前神经元。

有效感受野

understanding the effective receptive field in deep convolutional neural network 一文中提出了有效感受野的理论，论文发现并不是感受野内所有像素对输出向量的贡献相同，在很多情况下感受野区域内像素的影响分布是高斯分布，有效感受野仅占理论感受野的一部分，且高斯分布从中心到边缘快速衰减，下图第二个是训练后CNN的典型有效感受野。

我们看到绿色这个区域，黄色为图像，绿色框扫过时，对于第一例是只扫过一次，也就是参与一次运算，而后面靠近中心区域的列则均是参与了多次计算。因此，最终实际的感受野，是呈现一种高斯分布。

感受野的范围越大表示其接触到的原始图像范围越大，也就意味着它能学习更为全局，语义层次更高的特征，相反，范围越小则表示其所包含的特征越局部和细节

常用的网络模型训练技巧？

1. 使用更大的batch size，可以加快训练进度，但是对于凸优化问题，收敛速度会随着batch size的增加而降低。所以在相同的epoch下，batch size更大可能会导致验证集的acc更低，所以可以使用以下技巧来解决问题

• 使用更大学习率，例如lr等于0.1 batch size 为256，当将batch size增大至b，需要将初始lr 增加至0.1b
• lr warm up

2. 使用更低的数值精度
3. cosine learning rate decay
4. label smoothing
5. knowledge distillation
6. mixup training， cutout， random erase等数据增强方法。

权重初始化

1. 权重初始化为0

如果将权重初始化全部为0，等价于一个线性模型，将所有权重设为0，对于每个w而言，损失函数的导数都是相同的，因此在随后的迭代过程中所有权重都具有相同的值，这样会使隐藏单元变得对称，并继续运行设置的n次迭代中，会导致网络中同一个神经元的不同权重都是一样的。

2. 随机初始化

如果X很大，w相对较大，会导致Z非常大，这样激活函数是sigmoid，就会导致sigmoid的输出值1或者0，到知道train不动，同时如果初始化均值为0，方差为1的高斯分布（训练过程参数分布会向两侧跑），当神经网络层数增多时，会发现越往后的层激活函数的输出值几乎为0，极易出现梯度消失。

3. Xavier 初始化

上面两种方法初始化权重极易出现梯度消失的问题，而xavier初始化可以解决上面的问题，其思想就是尽可能地让输入和输出服从相同地分布，这样就能避免后面层地激活函数地输出值趋向于0， xavier权重初始化比较适用于tanh和sigmoid激活函数，而对relu这种非对称性地激活函数还是容易出现梯度消失。权值采样(0, 1/N)的高斯分布。

4. kaiming初始化

主要解决relu层将负数映射到0，影响整体方差，kaiming初始化解决这个问题。权值采样为（0,2/N）的高斯分布。

5. 使用预训练模型的初始化参数

优化算法设计原理

优化算法采用的原理是梯度下降法，即最小化目标函数，最优化的求解过程，首先求解目标函数的梯度，然后将参数向负梯度方向更新，学习率表面梯度更新的步伐大小，最优化的过程依赖的算法称为优化器，深度学习优化器的两个核心是梯度与学习率，前者决定参数更新的方向，后者决定参数的更新程度。

Inception系列

v1——GoogLeNet: inception结构的主要贡献有两个：一是使用1 x 1的卷积来升降维；二是在多个尺度上同时进行卷积再聚合。

**v2和v3——BN-Inception：**v2在v1的基础上加入BN层，v3提出了四种inception模块，并引入辅助分类器，加速深度网络收敛，此外在网络中使用RMSProp优化器和标签平滑，并在辅助分类器中使用BN，进一步加速网络收敛。

主要核心思想：

• 用两个3x3的卷积代替5x5
• 用nx1 和 1xn卷积代替n x n卷积
• 两个3x3中的一个分解成1x3 和 3x1并行，用来平衡网络的宽度和深度
• 引入辅助分类器，加速深度网络收敛
• 避免使用瓶颈层

**v4：**研究了Inception模块与残差连接的结合。ResNet结构大大加深了网络深度，还极大的提升了训练速度，同时性能也有提升。v4主要利用残差连接来改进v3结构。

**Xception：**谷歌在2017年在v3的基础上提出的，主要有以下亮点：1. 作者从v3的假设出发，解耦通道相关性和空间相关性，进行简化网络，推导出深度可分离。2. 提出了一个新的xception 网络。 xception提出的深度可分离卷积和 mobilenet中是有差异的。（这里先1x1 pw，然后 3x3 dw， 效果差不多）

MobileNet系列

v1: 主要亮点有两个，第一个 采用depthwise convolution和 pointwise convolution 来大大减少计算量和参数量 ， 第二个增加超参数α和β来控制网络模型。

v2：针对V1中出现的DW部分卷积核容易失效，即卷积核参数大部分为零的问题，google团队在 2018年提出v2，相比于v1，准确率更高，模型更小。主要有以下两个亮点：使用inverted residual（倒残差结构 1x1升维 —> dw ---->pw， dw在高维空间效果可能更佳），使用了linear bottleneck（解决：卷积核参数大部分为0，主要是由于relu造成的。低维特征图做relu6运算，很容易造成信息的丢失，就将inverted 中最后一个relu6换成 线性激活函数）。

**v3：**在v2网络的基础上，主要有四个亮点

• 使用NAS确定网络结构
• 在v2的block基础上引入squeeze and excitation 结构（在inverted bottleneck结构中加入SE模块）
• 使用h-swish 激活函数来加快网络收敛速度，作为一个轻量化网络swish虽然能够带来精度提升，但是swish中sigmoid不容易求导的特性会使网络在移动端设备上的推理速度收到一定损失，因此作者对其进行改进，提出h-swish激活函数

$$swish(x)=x\cdot sigmoid(\beta x)$$

$$h-swish(x)=x\cdot \frac{ReLU6(x+3)}{6}$$

• 重新设计耗时层结构：开始的32个卷积核换成16个，实验结果证明精度几乎不变。

ShuffleNet系列

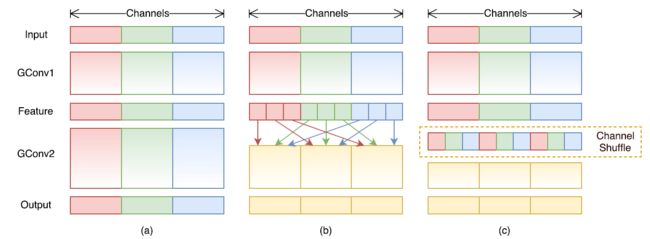
**v1：**旷视于2017年提出轻量级网络，主要有两个亮点：1. 提出pointwise group convolution 来降低PW卷积的计算复杂度， 2. 提出channel shuffle来改善跨特征通道的信息流动。

group convolution 的缺点：由于组和组之间没有交互，导致组与组之间信息流动阻塞，模型表达能力的弱化。这也是shuffleNet提出 channel shuffle的原因。 channel shuffle实现：假定输入层分为g组， 总通道数为g*n， 首先将通道那个维度拆分为(g,n)两个维度，然后将这个两个维度转置变成(n,g)，重新reshape成一个维度g x n，仅需要简单的维度操作和转置就可以实现均匀的shuffle。

第一步进行reshape：

第二步对得到的矩阵进行矩阵转置操作：

最后一步再进行reshape操作：

def shuffle_channels(x, groups):
    """shuffle channels of a 4-D Tensor"""
    batch_size, channels, height, width = x.size()
    assert channels % groups == 0
    channels_per_group = channels // groups
    # split into groups
    x = x.view(batch_size, groups, channels_per_group,
               height, width)
    # transpose 1, 2 axis
    x = x.transpose(1, 2).contiguous()
    # reshape into orignal
    x = x.view(batch_size, channels, height, width)
    return x

**v2：**同等复杂度下，比v1和mobilenet v2 更准确，主要有以下两个亮点：1. 提出四个高效网络设计指南 2. 针对v1的两种unit 做了升级。

• G1：卷积的输入输出具有相同channel的时候，内存消耗最小的。
• G2：过多的分组卷积操作会增大MAC，从而使模型速度变慢
• G3：模型内部分支操作会降低并行度（减少碎片化操作）
• G4：element-wise 不能被忽略。