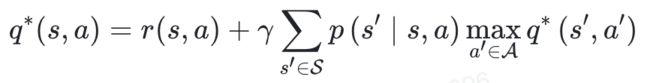强化学习(Reinforcement Learning,RL),是机器学习的基础范式和方法论之一。本文尝试通过对强化学习核心思想和原理的介绍,让读者能够快速掌握强化学习的基础,从而更好地开启下一阶段的学习。
01RL是什么?
强化学习(Reinforcement Learning,RL),又被称为激励学习、评价学习或者增强学习,是机器学习的范式和方法论之一;用于描述和解决智能体(agent)在与环境的交互过程中,通过学习策略达成回报最大化或者实现特定目标的问题。
机器学习的三大类别:
a. 监督学习
b. 无监督学习
c. 强化学习
图一 机器学习的三大类别
我们可以通过对狗的训练,来大概体会一下强化学习:
如果狗执行了我们的指令(action),我们就给予骨头等奖励(reward)
如果狗不执行我们的指令(action),我们就给予一些惩罚(负向的reward)
通过一定时间的强化(反复)训练,狗就学会了对指令的执行
图二 狗的训练对于狗的训练,可以看作一个单步(step)或者单幕(episode)的强化学习过程,而真实场景的RL,应该是多幕(episode)的(或者无限)。
注:强化学习中,每一步的信息可以用 <状态, 动作, 奖励> 的三元组表示,每一幕是指过程终止前的所有步的信息(也被称之为轨迹),这在下面的章节中会详细介绍。
02马尔可夫性质&马尔可夫决策过程
马尔可夫决策过程(Markov decision process,MDP)是强化学习的重要概念。要用强化学习解决一个实际问题,就需要把这个问题抽象为马尔可夫决策过程。马尔可夫决策过程,符合马尔可夫性质(Markov property)。
2.1 马尔可夫性质
什么是马尔可夫性质呢?当一个随机过程,某时刻的状态只取决于上一时刻的状态时,我们就称该随机过程具备马尔可夫性质(Markov property),用公式表示为 ![]()
换句话说,在给定现在的状态时,它的未来与过去状态是条件独立的。具备马尔可夫性质的随机过程,又称为马尔可夫过程(Markov process)。
2.2 马尔可夫决策过程(Markov decision process)
马尔可夫决策过程在马尔可夫性质的基础上增加了一个决策者控制;它提供了一个数学框架,用于结果部分随机部分受决策者控制影响的情况下对决策建模。某时刻的状态取决于上一个时刻的状态和所采取的行动,用公式表示为![]()

图四 马尔可夫决策过程
强化学习问题,可以抽象为马尔可夫决策过程,只是采取的每一个action,除了伴随着状态转移之外,还会得到一个reward。
03强化学习问题的构成元素
正如上面所说的,强化学习问题,在马尔可夫决策过程的基础上引入状态转移的奖励(reward)。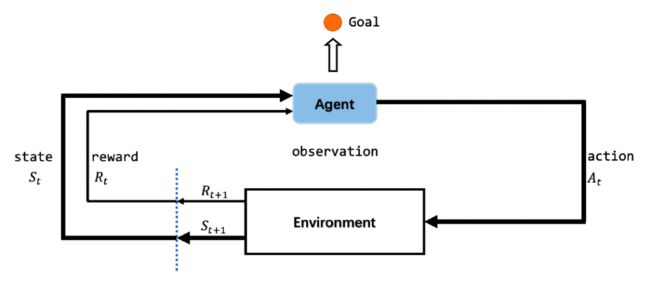
图五 强化学习的基本元素
基于上图,我们可以把RL的问题或者场景元素分为3大类:
1. 基本元素,可以理解为比较实体的元素
a. Agent
b. Environment
c. Goal(要实现的目标)
2. 主要元素,基于Markov process的抽象,构造求解的条件
a. State (包括当前的状态s和下一个时间步的状态 s')
b. Action
c. Reward
3. 核心元素,是RL问题求解的核心所在
a. Value(价值)
b. Policy(策略)
那么要用强化学习解决问题,就需要对policy和value有足够的了解。
04策略(Policy)&价值(Value)
我们先来明确几个术语:
○ (单步)奖励 reward,用r表示。
○ 多幕任务累积的reward,或者discounted reward,我们称之为回报(Return),用大写的来表示。可能是取自 Gain or Global Return 首字母
○ 状态变量空间和动作变量空间分别计作和。
4.1 策略(Policy)
从机器学习的角度看,我们首先要为智能体所采取的策略(Policy)抽象一个函数,从而进行后续的求解;Policy可以用函数:![]()
表示智能体在状态s下,采取动作α概率。不同的策略函数,影响到智能体对action的选择,action又会影响到状态的迁移和得到的reward以及最终的回报。
策略又分为确定性策略和随机策略,确定性策略只输出0和1,会有一个明确的action指示,要么执行要么不执行。而随机性策略,会输出一个概率值,是否采取某个action,还需要通过采样得到,所以随机性策略具备更好的探索能力。
4.2 价值(Value)
价值是从某个状态s出发,到多幕任务结束,能够获取到的回报的数学期望(因为是对未来的估计),价值函数很重要,因为智能体在状态s下的表现可以“有多好”,这个“有多好”就是通过价值函数来衡量。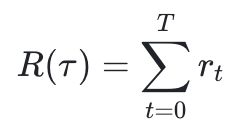
为了解决问题的方便,又把价值函数分为两种:状态-价值函数 和 状态-动作-价值函数。
4.2.1 状态价值函数我们把策略下状态的价值函数计作vπ(s),即从状态开始,智能体遵从策略能够得到回报的数学期望。
4.2.2 状态动作价值函数类似的,我们把策略下,由状态下采取动作的价值函数,计作 qπ(s, a),表示从状态s开始,采取动作能够得到回报的数学期望。
很明显我们可以写出二者的相互表示形式:

我们有了价值函数之后,就涉及到价值函数的最优化问题,这时候就需要引出贝尔曼方程了。
05贝尔曼方程
“贝尔曼方程(Bellman Equation)”也被称作“动态规划方程(Dynamic Programming Equation)”,由理查·贝尔曼(Richard Bellman)发现。贝尔曼方程是动态规划(Dynamic Programming)这种数学最佳化方法能够达到最佳化的必要条件。此方程将“决策问题在特定时间点的值”以“来自初始选择的报酬 及 由初始选择衍生的决策问题的值”的形式表示。藉这个方式将动态最佳化问题变成较简单的子问题,而这些子问题遵守由贝尔曼所提出的“最佳化原理”。引自:维基百科-贝尔曼方程。
简单说,贝尔曼方程把函数表示为递归的形式,从而用DP等手段进行求解。
5.1 价值函数的贝尔曼方程
我们首先推导出状态-价值函数vπ(s)的贝尔曼方程形式 :
如果从状态到状态‘的奖励是确定的,可以进一步简化。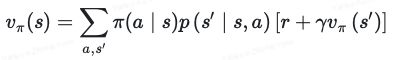
从上面的公式,我们可以得到两个信息:
• vπ(s)可以由下一个时刻的vπ(s')递归表示
• 对于每个三元组(, , )而言,首先计算( ∣ )(', ∣ , ),然后通过对价值进行加权平均得到。
同样的,我们也可以得到状态-动作-价值函数的贝尔曼方程形式:
5.2 最优价值函数的贝尔曼方程
强化学习的优化目标是找到一个最优策略 π使得智能体在一个多幕任务中可以得到最大的(期望)回报。在有限状态和动作集合的 MDP 中,至少存在一个策略比其他所有策略都好或者至少存在一个策略不差于其他所有策略,这个策略就是最优策略(optimal policy)。最优策略可能有很多个,我们都计作 π (s)。
我们可以得到两种最优价值函数的表达:最优-状态-价值函数
最优-状态-动作-价值函数
06求解最优策略
如果状态转移函数和奖励函数已知,那么可以用动态规划来求解最优策略了;但是实际上很多场景,并不能得到状态转移函数,那这个时候一般就采用蒙特卡洛方法,通过足够多的采样来逼近概率分布或者期望。
但是完整的蒙特卡洛方法又需要有足够多的样本,特别是对于高纬数据分布,每一步的数据量是很致命的,就会导致求解效率的低下。
我们可以从随机梯度下降或者小批量梯度下降的思想中找到一些灵感,我们不需要完整的蒙特卡洛采样,可以把动态规划和蒙特卡洛的思想结合,一步步地缩小求解问题的不确定性,这种方法也叫做时序差分。举个简单的例子来解释下时序差分的思想。
我们要预测北京到上海的距离(北京-上海),如果我们从北京开车出发到上海,那么一定是可以得到一个比较准确的距离。那如果我只开到了济南,这时候我仍然可以更新我们的(北京-上海)来降低它的不确定度(北京-上海)=d北京-济南+(济南-上海)。
6.1 动态规划
动态规划算法能够工作的前提是我们要知道MDP环境的完整模型:π(a∣s),即当前的策略(', ∣ , ),即状态转移模型和回报函数有两种典型的动态规划算法,这两种动态规划算法的思想,在TD中依然可以工作。
6.1.1 策略迭代Policy Iteration策略迭代算法,我们先选择一个随机的策略,然后我们通过策略评估和策略提升来进行不断的迭代,使得策略可以收敛到 πt+1=πt.
图七 策略迭代
上面提到了两个关键词,策略评估和策略提升;策略评估用来评定一个策略的效果,策略提升是在原有的策略上尝试寻找一个更好的策略,逐步找到最优的策略。
1. 一般可以用状态价值函数,来作为()的策略评估函数:
2. 可以证明贪心策略‘满足策略提升定理的条件,所以策略 '能够比策略更好或者至少与其一样好。我们可以直接贪心地在每一个状态选择动作价值最大的动作,也就是:
3. 整体的流程就是
6.1.2 价值迭代Value Iteration价值迭代算法更为直接,先通过迭代得到最优状态-价值-函数,然后通过最优状态价值函数,直接恢复出最优策略π。假设我们已经得到了*(s) ,那么我们有:最优策略
*(s)的求解同样直接:
a.最优状态-价值函数的贝尔曼方程: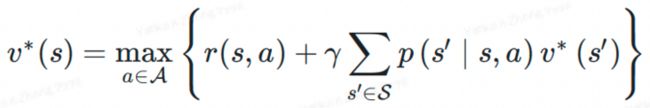
b. 单步递归式:
c.不断递归上面两步,直到到找贝尔曼方程的不动点
6.1.3 策略迭代Policy Iteration vs 价值迭代Value Iteration策略迭代Policy Iteration价值迭代Value Iteration随机策略开始随机的状态价值函数开始算法相对复杂算法相对简单收敛更快收敛慢一些
6.2 时序差分法
动态规划需要MDP环境的完整模型已知,时序差分法结合了蒙特卡洛和动态规划算法的思想,可以从样本数据中学习和估计策略的价值函数(蒙特卡洛),那么就可以使用DP的迭代思想来进行最优价值函数和策略的求解了(动态规划)。这种不需要知道模型的强化学习方法,又被称为model-free 。
下面我们来看下时序差分的价值函数预估方法,预估了v π(s)就可以进行策略评估了,接下来就可以进行策略提升了。
蒙特卡洛方法估计价值函数的方法是用策略在 MDP 上采样很多条序列,计算从这个状态出发的回报再求其期望就可以了。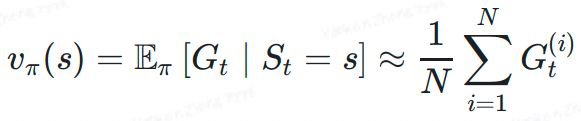
1. 使用策略完整的采样(直到流程结束);因为是完整流程采样,可以得到最终的回报,那么我们也很容易得到每一时间步之后的回报Gt。
2. 针对采样的每一步进行更新(类似梯度上升)。![]()
Gt表示时间步上得到的状态的回报。
3. 时序差分算法用当前获得的奖励加上下一个状态的价值估计来作为在当前状态会获得的回报(北京到上海的距离预估例子),即:
rt + γv (st+1) − v (st )称为时序差分误差。
另外,蒙特卡洛本身是无偏估计,但是时序差分在更新过程进行了多次预估,是有偏估计,所以出现了Double Q-learning这种通过样本划分,来纠正偏差的学习方法。
6.3 策略梯度方法
前面介绍的策略迭代和价值迭代中,对价值的建模是必不可少的。相对地,本节介绍的策略梯度方法则另辟蹊径,直接计算策略的梯度来对策略进行优化。从统计意义上来看,策略梯度方法的优化目标是价值函数关于状态的期望: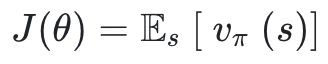
RL 训练的实质是在解决如下优化问题(其中θ为策略网路的参数):
每一个训练迭代中,如果我们知道优化目标关于网络参数的梯度: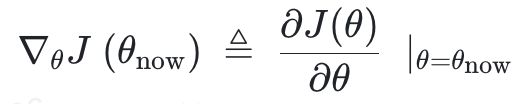
那么我们就可以使用这个梯度来提升我们的优化目标,进而让网络参数靠近最终我们期望的策略参数。根据策略梯度定理(的不严谨的表述),该梯度可如下计算:
(对推导过程等感兴趣的读者可以自行参考其他资料,如文献[5]的相关章节)直观上,可以如下理解策略梯度定理:从一对给定的状态s和动作,如果能获得一个正向的累计回报(即 qπ(s,)为正 ),那么说明给定的动作是“有益”的,即梯度的更新应当朝着使得让该动作的输出概率π(|s;θ)提升的方向进行。由于 自然对数函数的单调性,这等价于提升 ln π(a ∣ s; θ)。
基于梯度信息,优化器可以使用任何一种基于梯度的优化方法直接对策略网络的参数进行优化。
在不对价值函数进行建模的情况下,状态-动作-价值函数 qπ(s,)可通过蒙特卡洛近似完成,即:完成一幕(episode)探索,基于所有单步回报,计算出该幕中每一步的累计回报,并用该幕的累计回报来近似近似状态-动作-价值函数。这样的方法被称之为REINFORCE。
值得注意的是,蒙特卡洛近似存在方差过大的风险,即梯度的方向可能在邻近优化步之间发生剧烈抖动。为了缓解这个问题,策略梯度可以和前面介绍的方法进行组合。如 Actor-critic 方法中,使用神经网络对价值进行建模,可以理解为是策略梯度和价值学习的互补。使用神经网络建模的价值函数,由于神经网络的参数不会发生突变,因此输出也不会突变,从而缓解上述方差问题。
最后需要指出的一点是,策略梯度定理的推导过程中假设策略网络的参数为实时更新的参数,因此基于策略梯度定理的本节介绍的方法属于同轨策略(on-policy),即:用于完成探索的行为策略(behavior policy),和进行参数优化的目标策略(target policy),是相同参数的网络。同策略无法使用离线收集的数据,而与之相对的离轨策略(off-policy)则可以。
07经典RL算法
7.1 Q-learning
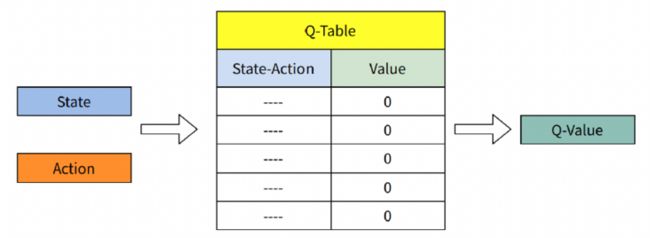
图九 Q-learningQ-learning 是一种著名的基于时序差分和查表法强化学习方法,属于确定性策略(贪婪)的方法,其Policy是 取状态-动作-价值函数 最大的动作,其策略更新就等价于(, )的更新了。
确定性策略的问题是会失去探索能力,所以一般采用 − 策略,在选择action的时候以小概率进行随机。Q-learning 先更新(t, t)【训练】,再以 − 来选择action【决策】;这种训练和决策序列不一致的方法属于off-policy (异轨策略);如果训练和决策序列一致,就属于on-policy(在轨策略或者同轨策略)。Sarsa就是一种和Q-learning类似的on-policy算法。
7.2 Sarsa
Sarsa 和 Q-learning 基本一样,唯一的区别是先通过 − 来选择好下一步的动作t+1,然后基于该动作来更新Q-Table(训练),训练序列和决策序列一致。![]()
7.3其他经典算法/高阶技巧概览
基于Q-Table的方案,只能容纳有限的状态和动作;而且如果动作和状态很多,基于Q-Table的方案也会失去一些泛化能力。因此,可以利用DNN的拟合和泛化能力,直接用状态-动作来学习“Q-Table”。
图十 DQNQ-learning 的更新规则是: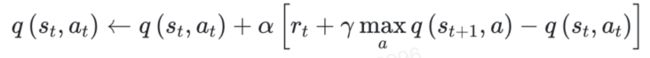
其目标是使得
靠得足够近,那么DQN的Loss function可以设定为二者的均方差形式: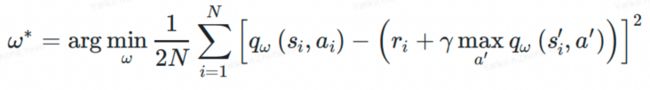
可以看到误差目标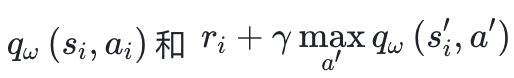
都包含神经网络的输出,更新网络参数的同时优化目标也在不断地改变,容易造成神经网络训练的不稳定。为了解决这一问题,DQN 便使用了目标网络(target network)的思想;即使用两套 Q 网络(训练网络和目标网络),用其中的目标网络单独计算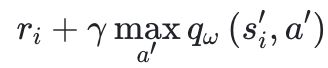
部分,目标网络的参数每N步才会与训练网络同步一次。Q-learning、Sarsa、DQN 都属于先学习价值函数,再基于价值函数得到最优策略(一般是基于e-greedy),这种方法属于value-base方法;也可以直接学习policy函数 πθ,那么就属于policy-base,policy-base相对于value-base有更好的探索能力。
7.4 其他经典算法/高阶技巧概览
除了经典的 RL 算法外,强化学习研究社区/工业界还提出了众多高阶技巧。这些高阶技巧结合经典/新提出的算法框架,缓解了强化学习中的各种问题(训练目标抖动、价值高估、稀疏奖励等),为强化学习研究的推进和工业界的成功实践做出了贡献。限于篇幅,下面简要列举其中有代表性的部分内容:算法/技巧作用做法策略梯度中引入基线REINFORCE with baselineA2C在训练过程中,减小随机梯度的方差,稳定训练
多价值网络TD3缓解高估问题实例化多组价值网络(相同结构,不同且独立的参数)计算 TD 目标的时候,使用所有(目标)价值网络中的最小值熵正则SAC鼓励训练阶段的探索目标函数中增加一项熵(推导后将以子网络损失、策略梯度额外项等途径进入训练过程)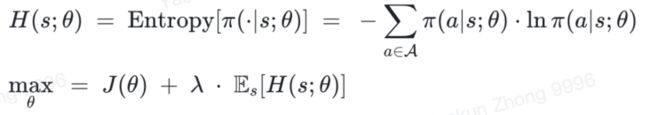
随机动作TD3鼓励训练阶段的探索在训练序列的生成过程中,对策略网络输出的动作上加入噪声进行扰动,鼓励探索更多的状态空间
参考文献 / 资料
[1].Sutton, Richard S., and Andrew G. Barto. "Reinforcement learning: An introduction." Robotica 17.2 (1999): 229-235.[2].https://www.analyticsvidhya.c...[3].https://arshren.medium.com/su...[4]. https://hrl.boyuai.com/chapte...[5].《深度强化学习》 王树森及其他, https://github.com/wangshusen...