3 Visual Perception for Self-Driving Cars 课程习题编程解答及笔记
自动驾驶课程 - The 3rd 视觉 - 课后答案及部分解释
- WEEK 1
-
- Module 1 Graded Quiz
- WEEK 2
-
- Visual Odometry for Localization in Autonomous Driving
- WEEK 3
-
- Feed-Forward Neural Networks
- WEEK 4
-
- Object Detection For Self-Driving Cars
- WEEK 5
-
- Semantic Segmentation For Self-Driving Cars
- WEEK 6
-
- Environment Perception For Self-Driving Cars
前言:这真的是很难得全方位介绍自动驾驶的组成到实现(理论上),专注于无人驾驶方向的课程算是头一个了(其他课程好像花钱的挺贵,Coursera真心算是为想自学的人提供了一个便捷的方法——可以通过15天的申请申请全部课程)
我建议大家还是申请官方的课程编程作业和自动驾驶仿真真的很有必要入一下,做一下,才能理解一些运动模型的建立过程,代码的实现吧。
- Coursera官方链接
- b站搬运不是很高清的 CC英文字幕 但是UP主有建github 下载了视频和课件可以去看看评论区获取吧。
尽管这样,我还是想强调一遍直接在Coursera申请助学金来听课是效果最好的,一来能督促自己(因为申请的课程是必须要通过的 不通过下次就不能申请其他课程了),二来编程作业只能通过会员/申请/付费来解锁。
希望这以下笔记,和解题答案思路等能给大家领个头,也一起共同学习进步,毕竟国内似乎还没有专门这么针对无人驾驶的课程专项。(为多伦多大学打call)
WEEK 1
Module 1 Graded Quiz
1.What is the most ACCURATE and PRECISE definition of the camera obscura?
A box or room with a pinhole aperture in front of an imaging surface
2.Which of the following statements are TRUE? Select all that apply.
Camera extrinsic parameters define the transformations from 3D world coordinates to 3D camera coordinates
Camera extrinsic parameters include a rotation matrix.
3.Imagine a situation in which a camera mounted on a car sees a point O O O on a signpost.
0.5,3.5,1
4.Variation 1
Based on the problem presented in the above question, what is the pixel location of the 2D projection of the point O on the image plane?
Please write your answer as a string with two comma-separated numbers without spaces (u and v), e.g. “100,100”
3.13,3.33
5.Why is camera calibration important in the self-driving car domain? Select all that apply.
Computed camera parameters can be used to correct for lens distortion
Computed camera parameters can be used to determine the camera location relative to the scene
Camera calibration estimates the parameters of the lens and image sensor of a camera
Computed camera parameters can be used to measure the size of a 2D object in 3D world units
6.Recall the camera calibration problem formulation, which has the following mathematical representation.
What methods from linear algebra can we use for solving this problem? Select all that apply.
Singular Value Decomposition
7.Let’s continue with the camera calibration formulation from the previous question.
What are some DISADVANTAGES of this linear calibration model? Select all that apply.
The linear model mixes the intrinsic and extrinsic camera parameters
The linear model does not allow for the incorporation of parameter constraints
Does not model radial distortion and other complex phenomena
8.If the baseline between camera centers is known for a stereo rig, what limitation of monocular vision can be avoided?
Inability to measure depth to a point
9.Consider a stereo camera setup in the figures below, similar to what you saw in the course slides.
Which of the statement about this configuration are correct? Select all that apply.
Z/X=f/xl
xr/f=b-X/Z
10.What parameters and computations are needed to perform depth calculations from disparity measurements? Select all that apply.
Need to compute the baseline, and the x and y offsets for the image center
Need to compute/know the focal length
11.A naive solution for the stereo correspondence problem is an exhaustive search, where we search the whole right image for a match to every pixel in the left image. Why is this a bad approach? Select all that apply.
This approach generally could not run in real time
The naive approach results in a large number of incorrect matches due to similar pixels in different parts of the image
12.What is the definition of an epipolar line for stereo cameras?
A line produced in one camera as a point in 3D space is moved along a single ray emanating from the other camera’s optical center
13.Recall that the first basic stereo algorithm which you saw in this module has four necessary steps. These steps are given to you below. Your task is to put them into correct order
CDBA
14.Which of the below statements about correlation and convolution are correct?
A convolution kernel is a 180 degrees rotated cross-correlation kernel
The order of multiplication of convolution kernels does not matter
A convolution filter and a cross-correlation filter are the same if the kernel is symmetric
15.Which of these 3X3 image filters is a Gaussian filter?
16
WEEK 2
Visual Odometry for Localization in Autonomous Driving
直接贴代码空白处,就不整个贴了,太多怕大家找的时候看不过来
def extract_features(image):
"""
Find keypoints and descriptors for the image
Arguments:
image -- a grayscale image
Returns:
kp -- list of the extracted keypoints (features) in an image
des -- list of the keypoint descriptors in an image
"""
### START CODE HERE ###
sift = cv.xfeatures2d.SIFT_create()
kp, des = sift.detectAndCompute(image,None)
### END CODE HERE ###
return kp, des
def extract_features_dataset(images, extract_features_function):
"""
Find keypoints and descriptors for each image in the dataset
Arguments:
images -- a list of grayscale images
extract_features_function -- a function which finds features (keypoints and descriptors) for an image
Returns:
kp_list -- a list of keypoints for each image in images
des_list -- a list of descriptors for each image in images
"""
kp_list = []
des_list = []
### START CODE HERE ###
for image in images:
kp,des=extract_features(image)
kp_list.append(kp)
des_list.append(des)
### END CODE HERE ###
return kp_list, des_list
def match_features(des1, des2):
"""
Match features from two images
Arguments:
des1 -- list of the keypoint descriptors in the first image
des2 -- list of the keypoint descriptors in the second image
Returns:
match -- list of matched features from two images. Each match[i] is k or less matches for the same query descriptor
"""
### START CODE HERE ###
# FLANN parameters
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50) # or pass empty dictionary
flann = cv.FlannBasedMatcher(index_params,search_params)
match = flann.knnMatch(des1,des2,k=2)
### END CODE HERE ###
return match
# Optional
def filter_matches_distance(match, dist_threshold):
"""
Filter matched features from two images by distance between the best matches
Arguments:
match -- list of matched features from two images
dist_threshold -- maximum allowed relative distance between the best matches, (0.0, 1.0)
Returns:
filtered_match -- list of good matches, satisfying the distance threshold
"""
filtered_match = []
### START CODE HERE ###
for f in match:
if f[0].distance / f[1].distance < dist_threshold:
filtered_match.append(f[0])
### END CODE HERE ###
return filtered_match
def match_features_dataset(des_list, match_features):
"""
Match features for each subsequent image pair in the dataset
Arguments:
des_list -- a list of descriptors for each image in the dataset
match_features -- a function which maches features between a pair of images
Returns:
matches -- list of matches for each subsequent image pair in the dataset.
Each matches[i] is a list of matched features from images i and i + 1
"""
matches = []
### START CODE HERE ###
matches = [match_features(d1, d2) for d1, d2 in zip(des_list[:-1], des_list[1:])]
### END CODE HERE ###
return matches
# Optional
def filter_matches_dataset(filter_matches_distance, matches, dist_threshold):
"""
Filter matched features by distance for each subsequent image pair in the dataset
Arguments:
filter_matches_distance -- a function which filters matched features from two images by distance between the best matches
matches -- list of matches for each subsequent image pair in the dataset.
Each matches[i] is a list of matched features from images i and i + 1
dist_threshold -- maximum allowed relative distance between the best matches, (0.0, 1.0)
Returns:
filtered_matches -- list of good matches for each subsequent image pair in the dataset.
Each matches[i] is a list of good matches, satisfying the distance threshold
"""
filtered_matches = []
### START CODE HERE ###
filtered_matches = [filter_matches_distance(m, dist_threshold) for m in matches]
### END CODE HERE ###
return filtered_matches
如果执行上面这步的话,务必将下面的改成 True
不然会报错
# Make sure that this variable is set to True if you want to use filtered matches further in your assignment
is_main_filtered_m = True
def estimate_motion(match, kp1, kp2, k, depth1=None):
"""
Estimate camera motion from a pair of subsequent image frames
Arguments:
match -- list of matched features from the pair of images
kp1 -- list of the keypoints in the first image
kp2 -- list of the keypoints in the second image
k -- camera calibration matrix
Optional arguments:
depth1 -- a depth map of the first frame. This argument is not needed if you use Essential Matrix Decomposition
Returns:
rmat -- recovered 3x3 rotation numpy matrix
tvec -- recovered 3x1 translation numpy vector
image1_points -- a list of selected match coordinates in the first image. image1_points[i] = [u, v], where u and v are
coordinates of the i-th match in the image coordinate system
image2_points -- a list of selected match coordinates in the second image. image1_points[i] = [u, v], where u and v are
coordinates of the i-th match in the image coordinate system
"""
rmat = np.eye(3)
tvec = np.zeros((3, 1))
image1_points = []
image2_points = []
### START CODE HERE ###
for m in match:
point1 = kp1[m.queryIdx].pt
point2 = kp2[m.trainIdx].pt
image1_points.append(point1)
image2_points.append(point2)
M, _ = cv2.findEssentialMat(np.array(image1_points), np.array(image2_points), k, method = cv2.RANSAC)
retval, R, t, _ = cv2.recoverPose(M, np.array(image1_points), np.array(image2_points), k, 30)
rmat = R
tvec = t
### END CODE HERE ###
return rmat, tvec, image1_points, image2_points
def estimate_trajectory(estimate_motion, matches, kp_list, k, depth_maps=[]):
"""
Estimate complete camera trajectory from subsequent image pairs
Arguments:
estimate_motion -- a function which estimates camera motion from a pair of subsequent image frames
matches -- list of matches for each subsequent image pair in the dataset.
Each matches[i] is a list of matched features from images i and i + 1
des_list -- a list of keypoints for each image in the dataset
k -- camera calibration matrix
Optional arguments:
depth_maps -- a list of depth maps for each frame. This argument is not needed if you use Essential Matrix Decomposition
Returns:
trajectory -- a 3xlen numpy array of the camera locations, where len is the lenght of the list of images and
trajectory[:, i] is a 3x1 numpy vector, such as:
trajectory[:, i][0] - is X coordinate of the i-th location
trajectory[:, i][1] - is Y coordinate of the i-th location
trajectory[:, i][2] - is Z coordinate of the i-th location
* Consider that the origin of your trajectory cordinate system is located at the camera position
when the first image (the one with index 0) was taken. The first camera location (index = 0) is geven
at the initialization of this function
"""
trajectory = np.zeros((3, 1))
### START CODE HERE ###
trajectory = [np.array([0, 0, 0])]
T = np.eye(4)
for i, match in enumerate(matches):
rmat, tvec, _, _ = estimate_motion(match, kp_list[i], kp_list[i+1], k, depth_maps[i])
Ti = np.eye(4)
Ti[:3, :4] = np.c_[rmat.T, -rmat.T @ tvec]
T = T @ Ti
trajectory.append(T[:3, 3])
trajectory = np.array(trajectory).T
### END CODE HERE ###
return trajectory
最后的结果提交:
Trajectory X:
[[ 0.00000000e+00 -8.70245060e-02 -9.33355830e-02 -3.25711111e-03
-2.08194217e-02 2.19703444e-02 -8.83708275e-02 -2.23557918e-01
-3.54546020e-01 -3.46869822e-01 -4.90872060e-01 -5.75799162e-01
-6.46158480e-01 -8.53958045e-01 -1.31974624e+00 -1.68693550e+00
-2.09049454e+00 -2.45790662e+00 -2.86968851e+00 -3.22965294e+00
-3.56188498e+00 -3.92631923e+00 -4.40741863e+00 -4.91117589e+00
-5.43706148e+00 -6.03109920e+00 -6.48371894e+00 -6.95880766e+00
-7.42686143e+00 -7.96121314e+00 -8.56932074e+00 -9.22441911e+00
-9.93857358e+00 -1.07403227e+01 -1.15753022e+01 -1.24444817e+01
-1.33547220e+01 -1.43082666e+01 -1.52895527e+01 -1.62798171e+01
-1.72704941e+01 -1.82673107e+01 -1.92669516e+01 -2.02643706e+01
-2.12636551e+01 -2.22474877e+01 -2.31514856e+01 -2.40933230e+01
-2.50197571e+01 -2.58905933e+01 -2.66827957e+01 -2.74510089e+01]]
Trajectory Y:
[[ 0. 0.02641833 -0.01363709 -0.00990824 0.01200632 0.03238468
-0.01232806 0.04097785 0.08446111 0.09703021 0.08305687 0.20493528
0.13430253 0.07343848 0.09100039 0.08269431 0.08695161 0.14667355
0.16067531 0.22084613 0.25603284 0.25294783 0.28320201 0.32135322
0.3095378 0.34754623 0.31002053 0.33575898 0.359157 0.4309403
0.53652281 0.58022714 0.64565108 0.64595104 0.67301181 0.71298607
0.73712317 0.77759518 0.81723228 0.87489569 0.92863503 0.99014944
0.98034523 0.97904382 0.99032839 0.98653668 1.00937804 1.00839101
1.05906023 1.05469078 1.10773637 1.15175402]]
Trajectory Z:
[[ 0. 0.99585582 1.99503334 2.99096104 3.99056662 4.98944286
5.98233037 6.9717155 7.96214536 8.96203691 9.95151561 10.94042058
11.93543846 12.9117145 13.79643645 14.72654562 15.64148932 16.56962813
17.48080299 18.41182666 19.35436779 20.2855918 21.16173565 22.02473803
22.87521128 23.67875004 24.56966373 25.44922512 26.33261529 27.17482394
27.961626 28.7159045 29.41282853 30.01048923 30.56010446 31.05298272
31.46635909 31.76487988 31.9533119 32.08000562 32.20519048 32.25591179
32.23097618 32.15918716 32.19528767 32.374338 32.80126426 33.13733165
33.51036321 34.00191716 34.60986576 35.24854482]]
WEEK 3
这个系列的机器学习和深度学习建议听同网站Coursera的吴恩达的两门课,深入浅出,大学生应该都能听得懂!但是卷积可能有点难抽象,大家示自己情况选择即可。
Feed-Forward Neural Networks
1.A feedforward neural network has an input layer, 5 hidden layers and an output layer. What is the depth of this neural network?
6
2.During training, the training data specifies the exact form of the hidden layers of a neural network.
False
3.Implement the ReLU activation function using numpy by replacing None in the code bellow.
import numpy as np
def ReLU(x):
y = np.maximum(0,x)
return y
注意这个因为输入的是一个数组,矩阵等,所以必须使用numpy中的maximum
4.The main building blocks of a machine learning system are: (Check all that apply.)
An Optimization Procedure
A loss function
A model
5.Which output unit/loss function pair is usually used for regression tasks that use neural networks?
Linear output units with Mean Squared Error Loss
6.The softmax output layer with cross-entropy loss is used to model the mean of a Gaussian distribution.
False
7.Which of the following might be used as a stopping condition for gradient descent. (Check all that apply.)
The number of iterations or epochs
The magnitude of the change in parameter values
The magnitude of change in loss function value
8.How are neural network bias parameters usually initialized at the beginning of training?
Initialized to 0.
9.Using all samples to estimate the gradient of the loss function with respect to the parameter results in less than linear return in accuracy of this estimate.
True
10.You are working on a self-driving car project and want to train a neural network to perform traffic sign classification. You collect images with corresponding traffic sign labels, and want to determine the number of frames you will use for training. Given that you have around one million images with labels, what training/validation/testing data split would you use?
96% training, 2% validation, 2% testing.
11.You finish training your traffic sign classifier, and want to evaluate its performance. You compute the classification accuracy on the training, validation, and testing data splits and get the following results:
Train your neural network longer.
Add more layers to your neural network.
12.When a neural network overfits the training data, the generalization gap is usually very small.
False
13.Which of the following strategies are used for regularization in neural networks? (Check all that apply.)
Dropout
Norm Penalties
Early Stopping
14.Dropout significantly limit the type of neural network models that can be used, and hence is usually used for specific architectures.
False
15.The name convolutional neural networks comes from the fact that these neural networks use a convolution operation instead of general matrix multiplication.
False
16.The input to a pooling layer has a width, height and depth of 224x224x3 respectively. The pooling layer has the following properties:
112
17.Using convolutions might reduce overfitting, as the number of parameters in convolutional layers is less than the number of parameters in fully connected layers.
True
WEEK 4
Object Detection For Self-Driving Cars
1.The object detection problem is defined as the locating objects in the scene, as well as classifying the objects’ category.
True
2.The problem of object detection is non-trivial. Which of the following statements describe reasons for the difficulty in performing object detection? (Check all that apply.)
Scene illumination is highly variable on road scenes.
Extent of objects is not fully observed.
Object size gets smaller as objects move farther away in a road scene.
3.You are a self-driving car perception engineer developing an object detector for your self-driving car. You know that for your object detector to be reliable enough to deploy on a self-driving car, it should have a minimum precision of 0.99 and a minimum recall of 0.9. The precision and recall are to be computed at a score threshold of 0.9 and at an IOU threshold of 0.7.
You compute the IOU of your detector on a frame with ground truth to find out the following:
No
4.The width and height of the output of a convolutional feature extractor are usually an order of magnitude higher than those of its input.
False
5.The input to a convolutional layer has a width, height and depth of 224x224x3 respectively. The convolutional layer has the following properties:
256
6.When designing convolutional architectures for object detection, max pooling layers are usually placed in which of the following building blocks:
Convolutional feature extractor
7.What type of output layer is most commonly used in the regression head of a convolutional object detector?
Linear Layer
8.Prior anchor boxes are usually sampled at random in image space before being used in the output layers of an object detector.
False
9.While training an object detector, the cross entropy is calculated for the negative anchors only.
True
10.When training an object detection model, the regression loss has the form:
1
11.During non-maximum suppression, the output bounding box list is sorted based on the value of every member’s:
Softmax output score
12.In context of self-driving cars, the output of object detectors can be used as a prior to perform which of the following tasks? (Check all that apply.)
3D object detection
Traffic light state estimation
Object tracking
13.One of the main advantages of using the output of 2D object detectors as a prior to 3D object detection is their ability to easily handle occlusion and truncation.
False
14.Sudden camera motion is detrimental to the performance of object trackers. This is because tracking usually assumes gradual change in the camera’s pose relative to the scene.
True
WEEK 5
Semantic Segmentation For Self-Driving Cars
1.Achieving smooth category boundaries is a major difficulty to take into account while designing semantic segmentation models. Which of the following statements describe the origins of this problem? (Check all that apply.)
The similarity in appearance between some categories such as road, curb, and sidewalk.
Thin objects such as poles, tree trunks, and lane separators.
2.When comparing the results of a semantic segmentation model to the ground truth, you found out that for the car category, its class IOU is 0.75. Knowing that the number of false positives (FP) is 17, and the number of false negatives (FN) is 3, what is the number of true positives achieved by this model?
60
3.To measure the performance of a semantic segmentation model over all classes, a good idea would be to average the class IOU.
False
4.Which of the following do you typically see in a Semantic Segmentation Model? (Check all that apply.)
Multiple Convolutional layers followed by an up-sampling layer.
Up-sampling layers in the decoder stage of the architecture.
Multiple Convolutional layers followed by a Pool layer.
5.Anchor boxes are an essential component of any semantic segmentation neural network architecture.
False
6.In your semantic segmentation model an input feature map is passed through a nearest neighbor up-sampling layer. The output feature map’s depth is equal to that of the input feature map.
True
7.A standard semantic segmentation architecture that uses a softmax output layer is allowed to associate multiple categories to a single pixel in the input image.
False
8.Which of the bellow loss functions is usually used to train semantic segmentation models?
Cross-Entropy Loss
9.A semantic segmentation model uses the following decoder architecture. The convolutions are all 3x3, have a padding size of 1, and have a number of filters shown in the figure. The up-sampling multiplier S is 2 for all upsampling layers.
8M, 8N, 64*D
10.In context of self-driving cars, semantic segmentation can be used to perform: (Check all that apply.)
Constrain the image space used to perform 2D object detection.
Lane boundary estimation.
Drivable space estimation.
11.Which of the following categories in a semantic segmentation output map would be useful to determine lane boundaries?
Lane Separator
Sidewalk
Curb
12.To estimate a plane model, an algorithm would require a minimum of:
Three points, chosen to be non-collinear.
13.To estimate lines that could belong to lanes in a post-processed output image from semantic segmentation, containing only relevant categories, one would:
First apply Canny edge detection followed by Hough transform line estimation.
WEEK 6
Environment Perception For Self-Driving Cars
写清楚参考课程和过程吧
- Driveable space estimation in 3D:
- Get x,y,z coordinates of pixels from depth: M1L3
- Estimate the road plane from segmentation output:M5L3
第一个是把深度相机的照片信息转换为x,y,z的坐标,主要用到转换方程和立体相机的校正矩阵K
Image coordinates to pixel coordinates:
[ x y z ] → [ u v 1 ] = 1 z [ x y z ] \left[ {\begin{array}{cc} x\\ y\\ z \end{array}} \right] \to \left[ {\begin{array}{cc} u\\ v\\ 1 \end{array}} \right] = \frac{1}{z}\left[ {\begin{array}{cc} x\\ y\\ z \end{array}} \right] ⎣⎡xyz⎦⎤→⎣⎡uv1⎦⎤=z1⎣⎡xyz⎦⎤
You will be using the equations learned in module 1 to compute the x, y, and z coordinates of every pixel in the image. As a reminder, the equations to get the required 3D coordinates are:
z = d e p t h z = depth z=depth
x = ( u − c u ) ∗ z f x = \frac{(u - c_u) * z}{f} x=f(u−cu)∗z
y = ( v − c v ) ∗ z f y = \frac{(v - c_v) * z}{f} y=f(v−cv)∗z
这样子,计算过程就明了了,首先是对图片像素点进行循环,[i,j]像素点等于的(i+1-u-c)*z/f,i+1是由于数组以0开始的原因,z是depth此像素点的深度信息,注意是depth[i,j],代码如下:
# GRADED FUNCTION: xy_from_depth
def xy_from_depth(depth, k):
"""
Computes the x, and y coordinates of every pixel in the image using the depth map and the calibration matrix.
Arguments:
depth -- tensor of dimension (H, W), contains a depth value (in meters) for every pixel in the image.
k -- tensor of dimension (3x3), the intrinsic camera matrix
Returns:
x -- tensor of dimension (H, W) containing the x coordinates of every pixel in the camera coordinate frame.
y -- tensor of dimension (H, W) containing the y coordinates of every pixel in the camera coordinate frame.
"""
### START CODE HERE ### (≈ 7 lines in total)
# Get the shape of the depth tensor
x=np.zeros(depth.shape)
y=np.zeros(depth.shape)
# Grab required parameters from the K matrix
f=k[0,0]
u=k[0,2]
v=k[1,2]
# Generate a grid of coordinates corresponding to the shape of the depth map
# Compute x and y coordinates
for i in range(depth.shape[0]):
for j in range(depth.shape[1]):
x[i,j]=(j+1-u)*depth[i,j]/f
y[i,j]=(i+1-v)*depth[i,j]/f
### END CODE HERE ###
return x, y
这里需要特别注意的是depth.shape[0]是y方向,depth.shape[1]是x方向的!!!不改的话 这一节可以得出正确的,但是下一节会一直得不出正确的答案。也会影响最终的结果。
[ 0.97 -0.02 0.24 -1.36]
Estimate the road plane from segmentation output:M5L3
Exercise: Implement RANSAC for plane estimation. Here are the 6 steps:
- Choose a minimum of 3 points from xyz_ground at random.
- Compute the ground plane model using the chosen random points, and the provided function compute_plane.
- Compute the distance from the ground plane model to every point in xyz_ground, and compute the number of inliers based on a distance threshold.
- Check if the current number of inliers is greater than all previous iterations and keep the inlier set with the largest number of points.
- Repeat until number of iterations ≥ \geq ≥ a preset number of iterations, or number of inliers ≥ \geq ≥ minimum number of inliers.
- Recompute and return a plane model using all inliers in the final inlier set.
这个就有点复杂了,一个个写不太连续,大家就按着他的步骤阅读,对于转置的操作是由它文档里写的输入参数的格式决定的。
Step 1:Choose a minimum of 3 points from xyz_data at random,用到的函数是:
numpy.random.choice()
numpy.random.choice(a, size=None, replace=True, p=None)
具体参数信息请参考:https://numpy.org/devdocs/reference/random/generated/numpy.random.choice.html?highlight=random%20choice#numpy.random.choice
a:1-D array-like or int
If an n darray, a random sample is generated from its elements. If an int, the random sample is generated as if a were np.arange(a)
# GRADED FUNCTION: RANSAC Plane Fitting
def ransac_plane_fit(xyz_data):
"""
Computes plane coefficients a,b,c,d of the plane in the form ax+by+cz+d = 0
using ransac for outlier rejection.
Arguments:
xyz_data -- tensor of dimension (3, N), contains all data points from which random sampling will proceed.
num_itr --
distance_threshold -- Distance threshold from plane for a point to be considered an inlier.
Returns:
p -- tensor of dimension (1, 4) containing the plane parameters a,b,c,d
"""
### START CODE HERE ### (≈ 23 lines in total)
n=xyz_data.shape[1]
# Set thresholds:
num_itr = 100 # RANSAC maximum number of iterations
min_num_inliers = n*0.99 # RANSAC minimum number of inliers
distance_threshold = 0.0001 # Maximum distance from point to plane for point to be considered inlier
max_num_inliers=0
max_inliers=[]
for i in range(num_itr):
# Step 1: Choose a minimum of 3 points from xyz_data at random.
choice=np.random.choice(n,3,replace=False)
points=xyz_data[:,choice]
# Step 2: Compute plane model
plane_parameters=compute_plane(points)
# Step 3: Find number of inliers
x=xyz_data[0,:].T
y=xyz_data[1,:].T
z=xyz_data[2,:].T
distance=dist_to_plane(plane_parameters.T, x, y, z)
inliers=xyz_data[:,distance<=distance_threshold]
# Step 4: Check if the current number of inliers is greater than all previous iterations and keep the inlier set with the largest number of points.
if inliers.shape[0]>min_num_inliers and inliers.shape[0]>max_num_inliers:
max_num_inliers=inliers.shape[0]
max_inliers = inliers
# Step 5: Check if stopping criterion is satisfied and break.
# Step 6: Recompute the model parameters using largest inlier set.
output_plane=compute_plane(inliers)
### END CODE HERE ###
return output_plane
- Lane Estimation:
- Estimating lane proposals using Hough transform:M5L3
主要是Canny和HoughLinesP的使用方法,opencv的手册里都有。
首先看一下官方的文档示例
import cv2
import numpy as np
img = cv2.imread('dave.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
edges = cv2.Canny(gray,50,150,apertureSize = 3)
lines = cv2.HoughLines(edges,1,np.pi/180,200)
void cv::HoughLinesP ( InputArray image,
OutputArray lines,
double rho,
double theta,
int threshold,
double minLineLength = 0,
double maxLineGap = 0
)
Python: lines = cv.HoughLinesP( image, rho, theta, threshold[, lines[, minLineLength[, maxLineGap]]] )
其中各个参数的解释:
- image:8-bit, single-channel binary source image. The image may be modified by the function.
- lines:Output vector of lines. Each line is represented by a 4-element vector (x1,y1,x2,y2) , where (x1,y1) and (x2,y2) are the ending points of each detected line segment.
- rho:Distance resolution of the accumulator in pixels.
- theta:Angle resolution of the accumulator in radians.
- threshold:Accumulator threshold parameter. Only those lines are returned that get enough votes ( >threshold ).
- minLineLength:Minimum line length. Line segments shorter than that are rejected.
- maxLineGap:Maximum allowed gap between points on the same line to link them.
在做的时候将rho设置为了10,theta直接1度(np.pi/180),如果不太了解rho参数的可以设置成1,再设置成10,看一下得出的道路线有什么区别就能大概理解了(1的话,特别是8,9,10都试一下,线会断续)
# GRADED FUNCTION: estimate_lane_lines
def estimate_lane_lines(segmentation_output):
"""
Estimates lines belonging to lane boundaries. Multiple lines could correspond to a single lane.
Arguments:
segmentation_output -- tensor of dimension (H,W), containing semantic segmentation neural network output
minLineLength -- Scalar, the minimum line length
maxLineGap -- Scalar, dimension (Nx1), containing the z coordinates of the points
Returns:
lines -- tensor of dimension (N, 4) containing lines in the form of [x_1, y_1, x_2, y_2], where [x_1,y_1] and [x_2,y_2] are
the coordinates of two points on the line in the (u,v) image coordinate frame.
"""
### START CODE HERE ### (≈ 7 lines in total)
# Step 1: Create an image with pixels belonging to lane boundary categories from the output of semantic segmentation
landmark=np.zeros(segmentation_output.shape,dtype=np.uint8)
landmark[segmentation_output==6]=255
landmark[segmentation_output==8]=255
# Step 2: Perform Edge Detection using cv2.Canny()
Edge=cv2.Canny(landmark,100,200)# Second and third arguments are our minVal and maxVal respectively.
# Step 3: Perform Line estimation using cv2.HoughLinesP()
lines=cv2.HoughLinesP(Edge,rho=10,theta=np.pi/180,threshold=200,minLineLength=100,maxLineGap=50)
#lines = cv.HoughLinesP( image, rho, theta, threshold[, lines[, minLineLength[, maxLineGap]]] )
# Note: Make sure dimensions of returned lines is (N x 4)
lines=lines.reshape((-1,4))
### END CODE HERE ###
return lines
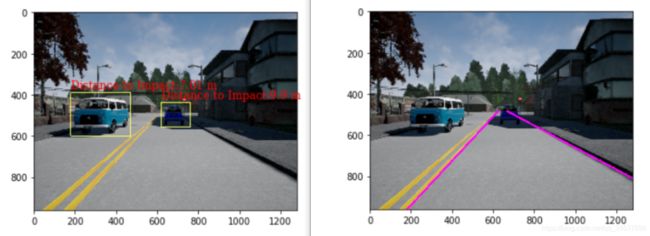
- Minimum Distance To impact Estimation:
- Estimating minimum distance to impact: M4L4
# Graded Function: find_min_distance_to_detection:
def find_min_distance_to_detection(detections, x, y, z):
"""
Filter 2D detection output based on a semantic segmentation map.
Arguments:
detections -- tensor of dimension (N, 5) containing detections in the form of [Class, x_min, y_min, x_max, y_max, score].
x -- tensor of dimension (H, W) containing the x coordinates of every pixel in the camera coordinate frame.
y -- tensor of dimension (H, W) containing the y coordinates of every pixel in the camera coordinate frame.
z -- tensor of dimensions (H,W) containing the z coordinates of every pixel in the camera coordinate frame.
Returns:
min_distances -- tensor of dimension (N, 1) containing distance to impact with every object in the scene.
"""
### START CODE HERE ### (≈ 20 lines in total)
distance=np.sqrt(x**2+y**2+z**2)
min_distances=[]
for detection in detections:
# Step 1: Compute distance of every pixel in the detection bounds
Class, x_min, y_min, x_max, y_max, score=detection
x_min,y_min,x_max,y_max=np.asfarray(x_min),np.asfarray(y_min),np.asfarray(x_max),np.asfarray(y_max)
x_min,y_min,x_max,y_max=int(x_min),int(y_min),int(x_max),int(y_max)
# Step 2: Find minimum distance
min_distances.append(np.min(distance[y_min:y_max,x_min:x_max]))
### END CODE HERE ###
return min_distances
最终的结果:
plane:
[-0.0, 1.0, 0.02, -1.36]
lanes:
[[1566.0, 960.0, 670.0, 484.0], [181.0, 960.0, 625.0, 484.0]]
min_distance
[7.01, 9.9]