蓝桥杯2015年第六届C/C++ B组省赛习题题解

目录

第一题：奖券数目

第二题：星系炸弹（日期计算）

第三题：三羊献瑞（全排列）

第四题：格子中输出

第五题：九数组分数（dfs）

 第六题：加法变乘法（枚举）

第七题：牌型种数（dfs+dp）

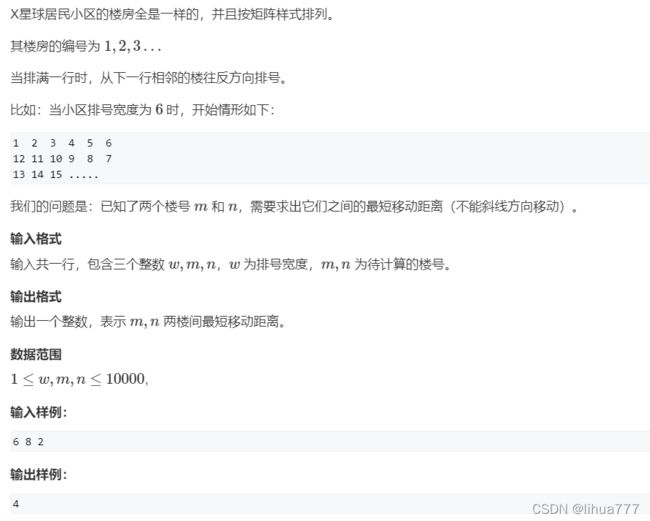
第八题：移动距离（数学+多情况+曼哈顿距离）

第九题：垒骰子（矩阵快速幂）

第十题：生命之树（dfs）

---

题目来源：

2015年第六届C/C++ B组蓝桥杯省赛真题_元气算法的博客-CSDN博客_2015年蓝桥杯c语言b组试题

---

第一题：奖券数目

#include
using namespace std;

bool check(int num)
{
	while (num)
	{
		int j = num % 10;
		if (j == 4) return false;
		num /= 10;
	}
	return true;
}

int main()
{
	int cnt = 0;
	for (int i = 10000; i <= 99999; i++)
	{
		if (check(i)) cnt++;
	}

	cout << cnt << endl;//52488

	return 0;
}

---

第二题：星系炸弹（日期计算）

 解析：

其实1000天也不难算，手算即可，但还是严谨的用代码给出答案

#include
using namespace std;
int months[13] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };
bool is_leap(int year)
{
	return (year % 400 == 0 || (year % 100 != 0 && year % 4 == 0));
}

int main()
{
	int year = 2014;
	int month = 11;
	int day = 9;
	
	int T = 1000;
	while (T--)
	{
		day++;
		if (month == 2)
		{
			if (is_leap(year)) months[2] = 29;//如果是闰年
		}
		if (day > months[month])//如果天数已经大于该月的天数时
		{
			if (month == 12)//如果该月是12月，那么就++年
			{
				year++;
				month = 1;//月份重新变为1
				day = 1;
			}
			else month++, day = 1;//否则只是月份++
		}
		months[2] = 28;//还原
	}

	printf("%d-%02d-%02d\n", year, month, day);//2017-08-05

	return 0;
}

---

第三题：三羊献瑞（全排列）

 解析：

由小学数学可知：

三：一定是数字1，这个不要问为什么，就是这样的，自己模拟一下

然后就是全排列找出所有的可能，然后进行对应数字之间的判断即可

#include
#include
using namespace std;

int main()
{
	int num[9] = { 0,2,3,4,5,6,7,8,9 };
	do {
		if (num[0] != 0)//数字的开头不能为0
		{
			int a = num[0] * 1000 + num[1] * 100 + num[2] * 10 + num[3];
			int b = 1000 + num[4] * 100 + num[5] * 10 + num[1];
			int c = 10000 + num[4] * 1000 + num[2] * 100 + num[1] * 10 + num[6];
			if (a + b == c)
			{
				cout << "1" << num[4] << num[5] << num[1] << endl;
				break;//1085
			}
		}
	} while (next_permutation(num, num + 9));

	return 0;
}

---

第四题：格子中输出

---

第五题：九数组分数（dfs）

#include 
void test(int x[])
{
	int a = x[0]*1000 + x[1]*100 + x[2]*10 + x[3];
	int b = x[4]*10000 + x[5]*1000 + x[6]*100 + x[7]*10 + x[8];
	
	if(a*3==b) printf("%d / %d\n", a, b);
}

void f(int x[], int k)
{
	int i,t;
	if(k>=9){
		test(x);
		return;
	}
	
	for(i=k; i<9; i++){
		{t=x[k]; x[k]=x[i]; x[i]=t;}
		f(x,k+1);
		_____________________________________________ // 填空处
	}
}
	
int main()
{
	int x[] = {1,2,3,4,5,6,7,8,9};
	f(x,0);	
	return 0;
}

解析：

我已经看到蓝桥杯的f函数就已经知道它是dfs了，没毛病啊兄弟们，毕竟还有个return，都知道是递归了，递归之后要还原，那么就要知道上一步是干什么，交换是吧，那么再交换一次就还原了，即可

所以答案是：{t=x[k]; x[k]=x[i]; x[i]=t;}

---

 第六题：加法变乘法（枚举）

#include 
using namespace std;

int main()
{
	for (int i = 1; i < 49; i ++)                                 // 枚举第一个 * 左边的数字
		for (int j = i + 2; j < 49; j ++)                         // 枚举第二个 * 左边的数字
		{
			if(1225 - 2*i-1 - 2*j-1 + i*(i+1) + j*(j+1) == 2015) 
			   cout << i << endl;
		}	
	
	return 0;
}  

---

第七题：牌型种数（dfs+dp）

 DFS：

#include
using namespace std;

int ans;

void dfs(int kind, int sum)
{
	if (sum > 13) return;
	if (kind == 14)
	{
		if (sum == 13) ans++;
		return;
	}
	for (int i = 0; i <= 4; i++)
	{
		dfs(kind + 1, sum + i);//这种类型，选多少张牌
	}
}

int main()
{
	dfs(1, 0);
	cout << ans << endl;
	return 0;
}

---

动态规划dp：

dp分析：

（1）dp数组的含义：dp[i][k]，i：牌的种类，共13种；k：剩余需要选取多少张牌

（2）dp数组的属性：方案数

（3）dp数组的递推公式：dp[i][k]=

<1>上一类牌，选了0张，dp[i-1][k];

<2>上一类牌，选了一张，dp[i-1][k+1];

<3>上一类牌，选了两张，dp[i-1][k+2];

<3>上一类牌，选了三张，dp[i-1][k+3];

<4>上一类牌，选了四张，dp[i-1][k+4];

这样枚举有些麻烦，所以用一层for循环代替

（4）dp数组的初始化：

由递推公式可知，必须要初始化一个dp[1][一个比较大的数]，那么这个比较大的数是多少呢？

对于第一类牌，可以拿0~4张，那么就有：

for(int i=9; i<=13; i++){
		num[1][i] = 1;

需要倒过来想：

（5）dp数组的遍历顺序：

无特殊要求，两层正序即可

（6）dp数组的返回值：

根据定义从前13类牌中选，当剩余需求排数为0时，即可满足题意要求

#include
using namespace std;
int dp[14][14];

int main()
{
	for (int i = 9; i <= 13; i++) dp[1][i] = 1;//当剩余9~13张要选时，均初始化方案数为1

	for(int i=2;i<=13;i++)//枚举牌的种类
		for(int k=0;k<=13;k++)//枚举剩余需要选的牌的数量
			for (int prek = k; prek <= k + 4 && prek <= 13; prek++)//只能选1~4张该种牌
			{
				dp[i][k] += dp[i - 1][prek];//该类牌的数量=原本+上一类牌选取的四种方案数
			}
	cout << dp[13][0] << endl;

	return 0;
}

---

第八题：移动距离（数学+多情况+曼哈顿距离）

#include 
#include 
#include 
using namespace std;

int main()
{
    int w, m, n;
    cin >> w >> m >> n;
    m --, n -- ;//为了对应

    int x1 = m / w, x2 = n / w;
    int y1 = m % w, y2 = n % w;
    if (x1 % 2) y1 = w - 1 - y1;//奇偶情况
    if (x2 % 2) y2 = w - 1 - y2;

    cout << abs(x1 - x2) + abs(y1 - y2) << endl;

    return 0;
}

---

第九题：垒骰子（矩阵快速幂）

第六届蓝桥杯【省赛试题9】垒骰子 ( 矩阵快速幂 )_i逆天耗子丶的博客-CSDN博客

 AcWing 1217. 垒骰子 - AcWing

---

第十题：生命之树（dfs）

 

解析：

[AcWing蓝桥杯]之复杂DP（C++题解）_lihua777的博客-CSDN博客

vector模拟单链表：

#include
#include
#include
using namespace std;

typedef long long ll;
const int N = 1e5 + 5;

int n, w[N];
ll f[N];
vectore[N];


void dfs(int u, int fa)
{
    f[u] = w[u];
    int len = e[u].size();
    for (int i = 0; i < len; i++)
    {
        int j = e[u][i];
        if (j != fa)
        {
            dfs(j, u);
            f[u] += max(0ll, f[j]);
        }
    }
    return;
}


int main()
{
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        cin >> w[i];
    }
    for (int i = 0; i < n - 1; i++)
    {
        int x, y;
        cin >> x >> y;
        e[x].push_back(y);
        e[y].push_back(x);
    }
    dfs(1, -1);
    ll res = f[1];
    for (int i = 2; i < n; i++)res = max(res, f[i]);
    printf("%lld",res);
}

---

数组模拟单链表：

#include 
#include 
#include 

using namespace std;

typedef long long LL;

const int N = 100010, M = N * 2;

int n;
int w[N];
int h[N], e[M], ne[M], idx;
LL f[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

void dfs(int u, int father)
{
    f[u] = w[u];
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (j != father)
        {
            dfs(j, u);
            f[u] += max(0ll, f[j]);
        }
    }
}

int main()
{
    scanf("%d", &n);
    memset(h, -1, sizeof h);

    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }

    dfs(1, -1);

    LL res = f[1];
    for (int i = 2; i <= n; i ++ ) res = max(res, f[i]);

    printf("%lld\n", res);

    return 0;
}