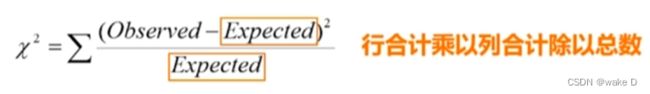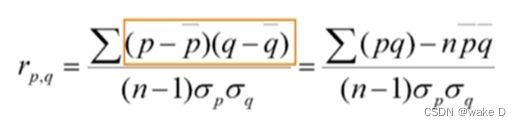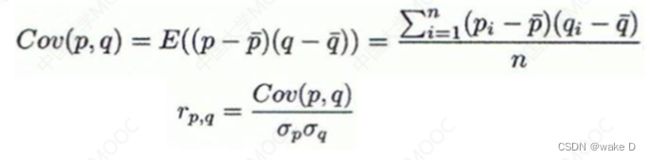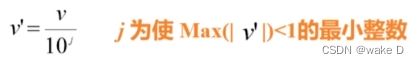文本数据挖掘----数据预处理

一、数据预处理简介

1、为什么要进行数据预处理

        一开始拿到的数据在数据的质量方面或多或少有一些问题，即在数据的准确性、完整性、一

致性、合时性（实时性）、可信性、解释性等方面可能存在问题，所以需要数据预处理来提高数据

的质量。

2、数据预处理的主要任务

        （1）数据清理（清洗）

                填写缺失值，平滑噪声数据，识别或者删除离群的数据，并搞定不一致的问题。

        （2）数据集成

                整合多个数据库、多维数据集或者文件。

        （3）数据缩减

                ①数据降维；

                ②数据压缩；

                ③Numerosity reduction；

        （4）数据转换和数据离散化

二、数据清洗

1、进行数据清洗的原因

        （1）脏数据

                有时候拿到的数据可能是“脏的”，即不完整的（缺少属性值，或者只包含总数据）；例

        如：职业=“ ”（丢失了数据）；

        （2）数据噪声

                即有些数据明显是错误的或者离群的；例：年龄=“-20”（显然就是错的）；

        （3）不一致的代码或者不符的名称

                例：年龄=“50”，生日=“13/4/1960”（出生于1960年的这个人，现在的年龄可能不是50

        岁，二者不一致）；

2、如何处理缺失的数据（脏数据）

        （1）忽略元组（删掉有缺失值的这一行）

                当类标号缺少的时候通常使用这种方法（监督式机器学习的训练集中缺乏这类的标

        签）；但是当每个属性的确实值比例比较大的时候，这种方法的处理效果就非常的差。

        （2）手工填写遗漏值

                缺点：工作量很大。

        （3）自动填写

                一般使用属性的平均值来填充空缺值。

        （4）具体处理方法（Python）

                具体的处理方法可以去下面这个网站看看，完整的教你用Python处理缺失的数据：

                6.4. Imputation of missing values — scikit-learn 1.1.2 documentation

3、如何处理噪声数据

        （1）箱线图监测离群数据（删除离群点）

                

4、如何处理不一致的代码或者名称数据

         通常通过计算推理、替换，全局替换。

三、数据集成

1、数据集成的作用

        将来自多个数据源的数据组合成一个连贯的数据源。

        

 2、数据集成面临的三个问题

        （1）模式集成

                整合来自不同来源的元数据，就是将相同类型字段数据的不同标签名进行合并成一个统

        一的标签名。

                例：

                 因为DBA中的cust-id和DBB中的cust-#的表述的含义是一样的属于同一类的数据，但是

        它们的标签名却不一样，所以模式集成就需要把它们的标签名统一，即如下所示：

                

        （2）实体识别

                就是同一个实体数据的表示方式不一样，需要统一表示方式；

                例：

                DBA中的name标签下的数据是汉字，而DBB中的name标签下的是拼音缩写，就像“张

        三”和“zs”表示的是同一个人，那么实体识别就要把“zs”替换成“张三“或者反过来。

                

        （3）数据的冲突检测和解决

                对同一个真实世界的实体，来自不同源的属性值，它们的表现方式不同，但是也表现的

        是同一个概念（有点类似实体识别的感觉），就像是不同的尺度单位之类的；

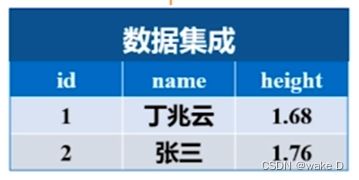
                例：

                DBA中的height和DBB中的height就表现的不一样，DBA中单位是米（m），而DBB的单

        位可能是英尺，最后就统一用米或者英尺其中一个来表示，如下图所示：

                

3、数据集成中的冗余信息的处理

        （1）冗余信息处理方法

                通常我们都会通过相关性分析和协方差分析可以检测到冗余的属性；

        仔细集成来自多个数据源，可能有助于减少或者避免冗余和不一致的地方，并提高读取速度

        和质量。

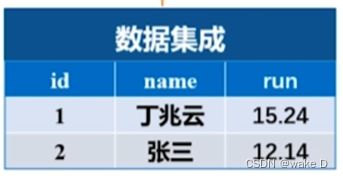
        例：

                 这两个数据库中分别有有跑3000m和5000m的数据，但是这两个数据都是对长跑能力的

        测试，所以就可以消除冗余的数据，把两个数据合并成一个。

                

        （2） 冗余信息处理的好处

                对于同一个内容的测定可能有两个或多个不同的表现形式在不同的数据源中，这时候就

        需要消除冗余数据，将两个或多个表现形式合并成一个，合并的好处就是：通常我们拿到的

        数据量都比较大，如果采用两列来表示同一个示例可能会占用过多的存储空间。

        （3）冗余处理方法之相关性分析

                ①卡方测试（离散变量）

                卡方检验适用于离散型变量不适用于连续型的；

                 

                的值越大，表示变量越有可能是相关的，即相关性越强；

                注：相关性并不意味着因果关系（即并不意味着，一个变量导致另一个变量怎么怎么样

        之类的）；

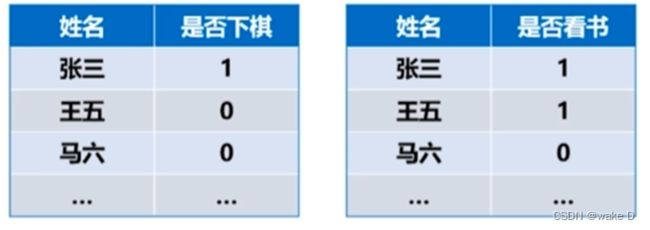
                例：

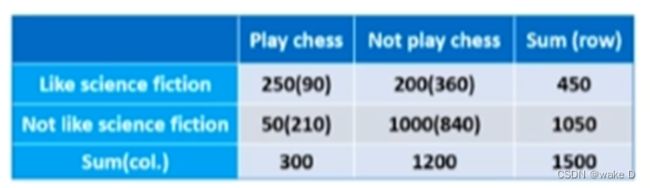
                 首先得出下面的分布矩阵：

 

                 这里的第一个250表示数据中两个表中都为1的有多少，第二个200表示第一个表里为0

        而第二个表里为1的有多少，第三个50表示第一个表里是1而第二个表里是0的有多少个，第四

        个1000表示第两个表里都是0的有多少个；

        注：括号里的是期望值，期望的算法就是上面的行乘以列除以总数；

                最后算得的值越大说明变量的相关性越大；

                ②皮尔逊相关系数（连续性变量）

                

                 其中n是元组的数目，而p和q是各自属性的具体值，和是各自的标准偏差；

                ③协方差

                 其中n是元组的数目，而p和q是各自属性的具体值，和是各自的标准偏差；

                 协方差除以一个标准差的积就等于皮尔逊相关系数；

                

                注：对于某些随机变量来说协方差为0，不一定表示它们相互独立；如果两组数据都服从

        相同的正态分布，那么此时协方差为0，就说明它们相互独立；

                例：

四、数据规约

1、进行数据规约的原因

        由于数据仓库可以储存TB级别的数据，所以在一个完整的数据集上运行的时候，复杂的数据

所花费的时间就比较长。

2、数据规约之数据降维

        （1）数据降维的功能

                就是把高维数据通过一些方法降为低维数据，以此来降低数据的复杂性。

        （2）降维的原因

                ①随着维数的增加，数据会变得越来越稀疏；

                例：

                 ②子空间的可能的组合将成倍增长；

                例：

                ③ 类似神经网络的机器学习方法，主要需要学习各个特征的权值参数。特征越多，需要

        学习的参数就越多，则模型越复杂；

                

                机器学习训练集的原则：如果模型越复杂，就需要更多的训练集来学习模型参数，否则

        模型将欠拟合；

                因此，如果数据集维度很高，而训练集数目很少，在使用复杂的机器学习模型的时候，

        首先选择降维。

                ④总结：需要降维的时候         

                数据稀疏，维度高；

                高维数据采用基于规则的分类方法；

                采用复杂模型，但是训练集数目较少的时候；

                需要可视化的时候；

        （3）数据降维的方法

                ①PCA主成分分析法

                主成分分析法就是设法将原来众多具有一定相关性的属性（比如p个属性），重新组合成

        一组相互无关的综合属性来代替原来属性。通常数学上的处理就是将原来p个属性作线性组

        合，作为新的综合属性。

 3、数据规约之降数据

        （1）什么是降数据

                就是数据规模非常大，如果直接用作训练的话，可能计算机的内存吃不消，或者需要尽

        快的出训练结果，就可以使用抽样（简单随机抽样，不放回抽样或有放回抽样）的方法将数

        据的规模减小；

                例：       4、数据规约之数据压缩 

        （1）理解   

                类似于将一张高清照片压缩为一个标清的图片，丢失了部分像素，但是降低了存储开

        销；

五、数据转换（规范化）和离散化 

1、数据转换（规范化）和离散化的概念

        函数映射：给定的属性值更换了一个新的表示方法，每个旧值与新的值可以被识别；

方法；

        

 2、规范化

        （1）为什么要进行规范化

                为了消除指标之间的量纲和取值范围差异的影响；

                例：就像高考在四川和北京的考生，比如某两个考生他们可能排名差不多，但是在北京

        和四川两个地方的排名范围不一样，由于排名的范围不同，所以不好比较，数据规范化就是

        为了解决这个问题。

        （2）数据规范化的方法

                ①最小-最大规范化

                

                 V就是需要规范化的数据，v‘就是规范化之后的数据；

                ②Z得分规范化

                

                如果是流式数据（即时时刻刻都有新数据进入），通常会使用z得分规范化（采用抽样来

        计算一个均值和标准差）；

                ③小数定标

                移动属性A的小数点位置（移动位数依赖于属性A的最大值）

                

                例：

                

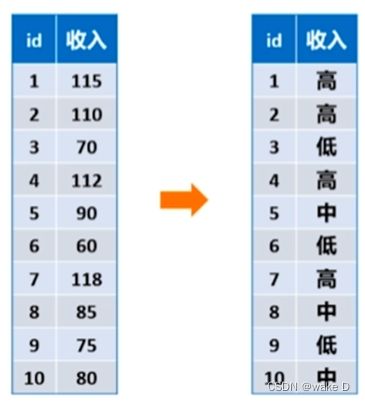
3、离散化

        （1）什么是数据离散化

                通过某种方法将原始的数值数据变成离散数据；

                例：

                

        （2）为什么需要离散化

                 部分数据发掘算法只适用于离散数据；

        （3）离散化方法（非监督离散）

                 ①等宽法

                根据属性的值域来划分，使每个区间的宽度相等。

                

                ②等频法

                 根据取值出现的频数来划分，将属性的值域划分成个小区间，并且要求落在每个区间的

        样本数目相等。

                例：

                ③聚类法

                 利用聚类将数据划分成不同的离散类别；