线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解

相关文章

1. K近邻算法和KD树详细介绍及其原理详解
2. 朴素贝叶斯算法和拉普拉斯平滑详细介绍及其原理详解
3. 决策树算法和CART决策树算法详细介绍及其原理详解
4. 线性回归算法和逻辑斯谛回归算法详细介绍及其原理详解
5. 硬间隔支持向量机算法、软间隔支持向量机算法、非线性支持向量机算法详细介绍及其原理详解

---

---

前言

  今天给大家带来的主要内容包括：线性回归算法、逻辑斯谛回归算法。废话不多说，下面就是本文的全部内容了！

---

一、线性回归

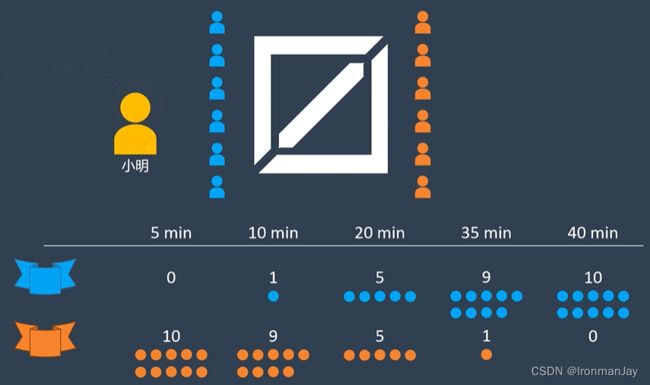
  假设小明现在有一个游戏战队，我们称其为蓝色战队，这支战队队员的游戏手感都比较慢热，在整个游戏比赛期间不同阶段的两个战队的得分情况如下所示：

图1：蓝色战队和橙色战队的得分情况

• 第5min：蓝色战队和橙色战队零十开
• 第10min：蓝色战队和橙色战队一九开
• 第20min：蓝色战队和橙色战队五五开
• 第35min：蓝色战队和橙色战队九一开
• 第40min：蓝色战队和橙色战队十零开

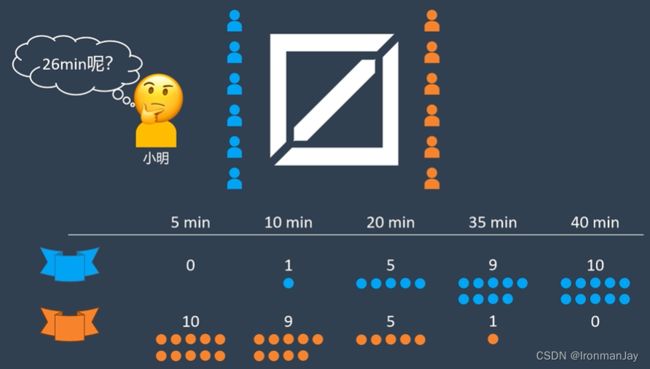
  由于游戏赛场上的情况变化莫测，作为游戏战队老板的小明想知道在比赛的第26min的时候，蓝色战队和橙色战队几几开呢？或者在比赛的其他时间，蓝色战队和橙色战队又是几几开呢？如果可以得到这样的数据，就可以帮助小明发掘他战队队员的最大潜力了。

图2：游戏比赛第26min蓝色战队和橙色战队的得分情况如何？

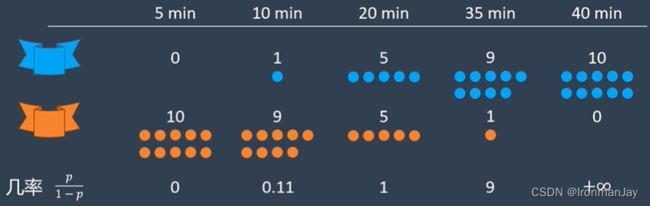
  为了得到以上信息，我们需要进行计算，在进行计算之前，首先我们要明确，几几开就代表着事情发生的几率，也就是蓝色战队赢下对局和输掉对局可能性的比值。我们把这些几率值列出来：

图3：在游戏比赛不同时间段的蓝色战队获胜的概率

  为了方便观察，我们把它转化为小数：

图4：将在游戏比赛不同时间段的蓝色战队获胜的概率转换为小数

  根据以上计算结果可以发现，当队伍十分可能输给对面的时候，赢的几率接近于零；当战队非常可能赢的时候，赢得几率接近于正无穷：

图5：将在游戏比赛不同时间段的蓝色战队获胜的概率刻画在数轴上

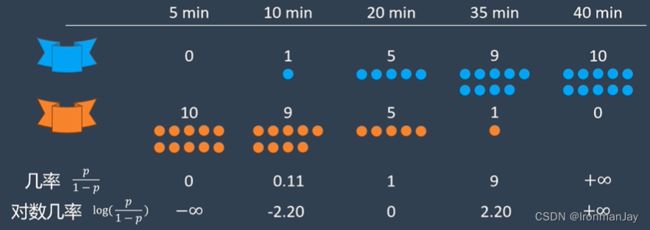
  虽然我们现在可以得到不同比赛时间的蓝色队伍获胜的概率分布情况，但是这种在正半轴十分不对称的分布不太好分析问题，所以我们使用几率的对数来分析数据：

图6：将在游戏比赛不同时间段的蓝色战队获胜的概率转换为对数概率

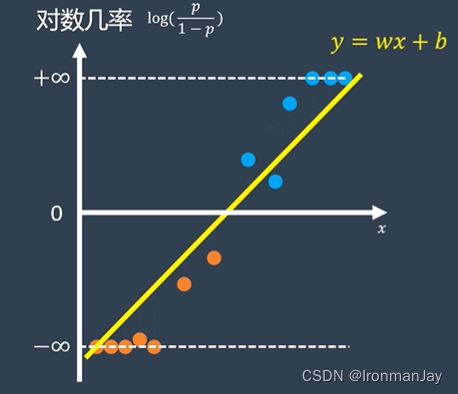
  可以看到，这样就可以把数据从正半轴重新映射回整条数轴上了：

图7：将在游戏比赛不同时间段的蓝色战队获胜的概率转换重新刻画在数轴上

  如果我们以对数几率作为$y$轴，比赛时间作为$x$轴，就可以把所有比赛的数据映射到$x\cdot y$平面上了：

图8：将在整场比赛中的数据映射到x·y平面上

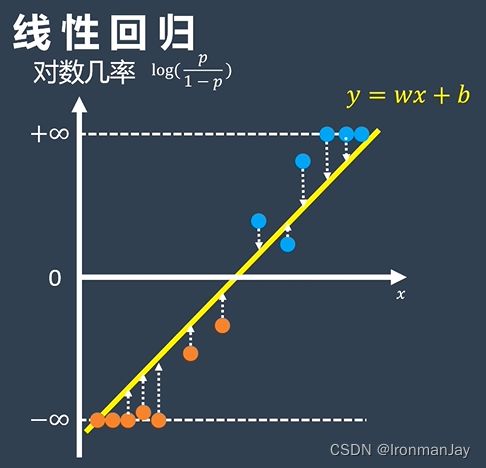
  可以发现，上图就是我们耳熟能详的线性回归。我们都知道，通过每一个点到直线的距离差，然后做一个最小二乘法的优化：
$$e(w,b)=\frac{1}{2}\sum _{i=1}^N||e_i|{|}^2$$
  利用上式进行最小二乘法的优化后，就可以得到一条最完美的直线来拟合这些数据，得到这条直线之后，我们只需要查询$x$轴所对应的时间，就可以求出赢下这场比赛的可能性了：

图9：使用最小二乘法得到对于整场比赛数据的最佳拟合直线

  以上就是对于线性回归的介绍。

二、逻辑斯谛回归

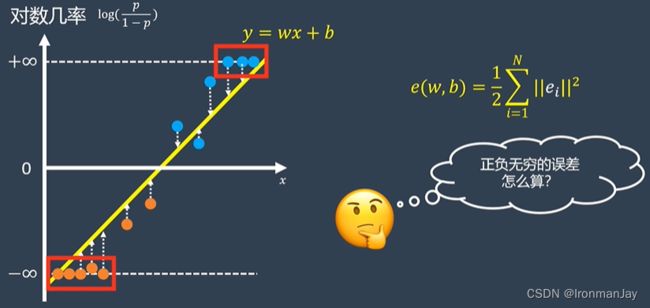
  虽然看起来我们可以得到比赛中不同时间段的蓝色队伍获胜的可能性，但是其中有许多数据点的$y$值是正负无穷，这种情况可是没有办法计算数据和直线的距离误差的：

图10：使用直线拟合数据无法计算正负无穷时数据和直线距离误差

  为了解决这个问题，我们可以考虑把这条直线重新映射回概率空间，我们是以对数几率作为$y$轴的，所以$y$的值为：
$$y=\log (\frac{p}{1-p})$$
  我们现在要把概率$p$写成$y$的函数，所以等式两边做一个自然对数的幂：
$$e^y=\frac{p}{1-p}$$
  然后等式两边同时乘以$1-p$：
$$(1-p)e^y=p$$
  把括号展开：
$$e^y-p{e}^y=p$$
  然后等式两边交换$p{e}^y$：
$$e^y=p+p{e}^y$$
  这样等式的右面就可以提出公共项$p$：
$$e^y=(1+e^y)p$$
  此时，我们就可以得到$p$的表达式：
$$p=\frac{e^y}{1+e^y}$$
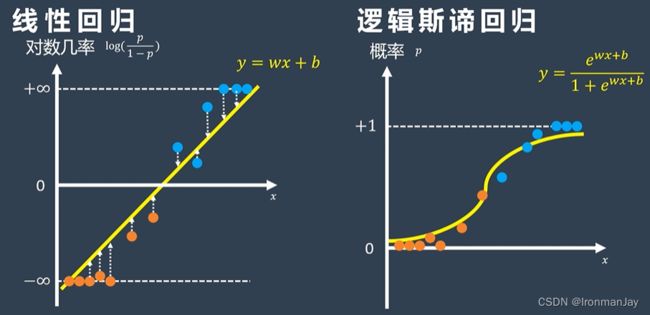
  上式就是逻辑斯谛函数，当我们把直线$y=wx+b$的表达式代入到公式中，就得到了概率空间的表达：
$$p=\frac{e^{wx+b}}{1+e^{wx+b}}$$
  上式就是逻辑斯谛回归的概率函数，因此，我们可以这样理解，概率空间内的逻辑斯谛回归，其实就是对数几率空间内的线性回归：

图11：线性回归和逻辑斯谛回归

  此时，我们已经可以在概率空间中讨论不同比赛时间的蓝色队伍获胜的可能性了：

图12：在概率空间讨论不同比赛时间的蓝色队伍获胜的可能性

  既然回到了概率空间，我们就可以使用概率论中的极大似然估计，来得到拟合情况最好的逻辑斯谛曲线。首先，我们假设对于在时间$x$时蓝色队伍赢下比赛的概率为$p$：
$$p(y=1|x)=p$$
  那么蓝色队伍在时间$x$时输掉比赛的概率就是$1-p$：
$$p(y=0|x)=1-p$$
  因为$y$的值只能取零或一，所以我们可以按照下式来表达任意样本$x_i$的概率：
$$p(y=?|x_i)=p_i^{y_i}(1-p_i{)}^{1-y_i}$$
  使用最大似然估计法得到的似然值就是这些样本概率的乘积：
$$L=\prod _{i=1}^{N}p(y=?|x_i)$$
  我们可以把$p(y=?|x_i)=p_i^{y_i}(1-p_i{)}^{1-y_i}$代入到上式中：
$$L=\prod _{i=1}^N{p}_i^{y_i}(1-p_i{)}^{1-y_i}$$
  一系列式子的乘积是一个不太容易优化的表达，所以我们取它的对数形式，把乘法转化为加法：
$$\log (L)=\sum _{i=1}^N{y}_i\log \left(p_i\right)+\left(1-y_i\right)\log \left(1-p_i\right)$$
  然后把括号展开整理一下：
$$\log (L)=\sum _{i=1}^N{y}_i\log \frac{p_i}{1-p_i}+\log \left(1-p_i\right)$$
  可以看到，在上式中，等号右面的式子中出现了$\log \frac{p_i}{1-p_i}$这个熟悉的身影，这就是之前我们介绍的对数几率，因为逻辑斯谛回归就是对数几率空间内的线性回归，所以我们可以将$\log \frac{p_i}{1-p_i}$替换成直线的方程：
$$\log (L)=\sum _{i=1}^N{y}_i(w{x}_i+b)+\log \left(1-p_i\right)$$
  需要注意的是，上式最后面的$p_i$值就是逻辑斯谛函数，所以我们将逻辑斯谛函数$p_i=\frac{e^{w{x}_i+b}}{1+e^{w{x}_i+b}}$代入上式即可：
$$\log (L)=\sum _{i=1}^N{y}_i(w{x}_i+b)-\log \left(1+e^{w{x}_i+b}\right)$$
  上式就是我们最终得到的式子，这个式子之和$w$和$b$这两个参数相关，我们可以使用最大似然估计优化方法得到最好的$w$和$b$这两个参数：
$$w,b=argma{x}_{w,b}\sum _{i=1}^N{y}_i(w{x}_i+b)-\log (1+e^{w{x}_i+b})$$
  当我们得到最优的参数$w$和$b$的值后，就可以将$x=26$代入：
$$p(26)=\frac{e^{w\times 26+b}}{1+e^{w\times 26+b}}$$
  这样就可以得到在比赛的第26分钟时，蓝色战队获胜的概率了：

图13：通过逻辑斯谛回归计算在比赛的第26min时蓝色队伍获胜的概率

以上就是逻辑斯谛回归的全部过程。

---

总结

  以上就是本文的全部内容了，这个系列还会继续更新，给大家带来更多的关于机器学习方面的算法和知识，下篇博客见！