数据预处理之归一化，标准化，数据降维之特征选择
- 归一化
以上为归一化的原理
接下来将展示出归一化的代码
from sklearn.preprocessing import MinMaxScaler
mm = MinMaxScaler()
data = mm.fit_transform([[90, 2, 10, 40],[60, 4, 15, 40],[75, 3, 13, 46]])
data
打印结果为：
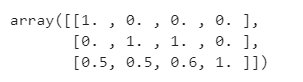
如果将上述代码的
**mm = MinMaxScaler()**改为
mm = MinMaxScaler(feature_range = (2, 3))
feature_range = (2, 3)意为将数据归一化后的范围为(2,3)
打印结果为：
- 标准化（注意标准化之后就不能用VarianceThreshold进行特征选择了，因为这是所有的特征列的方差都为1）
以上为标准化的原理
接下来将展示出标准化的代码
from sklearn.preprocessing import StandardScaler
std = StandardScaler()
data = std.fit_transform([[90, 2, 10, 40],[60, 4, 15, 40],[75, 3, 13, 46]])
data
打印结果为：
虽然归一化和标准化都可以将数据缩小为一定程度
但是归一化是将数据缩小到一定范围内，而标准化是将数据缩小成为均值为0，方差为1的数据
并且对于归一化来说，归一化容易受到异常点而产生的结果可能会发生改变，因为上文说了归一化的原理会用到最大值和最小值，如果出现异常点的话，最大值和最小值可能会发生改变，所以归一化不一定适用。
而对于标准化来说，标准化的原理会使用到平均值和方差，但是只要你具有一定的数据量，少量的异常点对于平均值和方差的影响并不大，所以标准化并不会出现较大的误差。
而在我们平常生活中所收集到的数据难免会有异常值，考虑到鲁棒性的问题，一般情况下尤其是在回归算法里面我们会使用标准化，很少使用归一化。
-
数据降维之特征选择
特征选择是什么：
特征选择就是单纯地从提取到的所有特征中选择部分特征作为训练集特征，特征在选择前和选择后可以改变值、也不改变值，但是选择后的特征维数肯定比选择前小，因为我们值选择了其中的一部分特征
特征选择的主要的三大方法：
1.Filter(过滤式)：VarianceThreshold
2.Embedded(嵌入式)：正则化、决策树
3.Wrapper(包裹式) -
VarianceThreshold
from sklearn.feature_selection import VarianceThreshold
# 删除低方差的特征，参数threshold为方差的阈值，即删除方差小于该值的特征
var = VarianceThreshold(threshold=0.0)
data = var.fit_transform([[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]])
data
打印结果为：
此处要注意threshold不能太大，如果太大的话数据全部删除掉了，那么就会报错：
No feature in X meets the variance threshold 3.00000此时我的参数threshold设置为了3.0
- PCA主成分分析法(一个大佬的提醒，PCA是特征抽取，不是特征选择)
本质：PCA是一种分析，简化数据集的技术
目的：使数据维度压缩，尽可能降低原数据的维度(复杂度),但是会损失少量的信息
作用:可以消减回归或者聚类分析中特征的数量
因为PCA会损失少量信息，所以一般当特征多于100时才会考虑是否要使用PCA
from sklearn.decomposition import PCA
# 参数n_components为保留后的特征信息量，一般值都为 0.9~0.95
# 此处意为保留 90%的特征
pca = PCA(n_components=0.9)
data = pca.fit_transform([[2, 8, 4, 5], [6, 3, 0, 8], [5, 4, 9, 1]])
data
打印结果如下：
本文章内容大部分来源于B站上的一个视频
链接: 【机器学习】特征工程