分别使用全连接神经网络和卷积层神经网络进行多分类问题

使用全连接神经网络

我们接下来就是要预测类似下面的图片中的数字是多少

导入之后会用到的模块

import torch
from torchvision import transforms, datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim

加载数据集，并且将数据集进行划分

batch_size = 64
transform = transforms.Compose([
    transforms.ToTensor(), # 将数据转换成张量
    transforms.Normalize((0.1307, ), (0.3081, )) # 将数据标准化为 0-1的值
])                                               # 0.1307为均值，0.3081位标准差

# 如果你已下载过数据集，则其中的root为数据集所在的地址，并且将download设置为False
# 如果你未下载过数据集，则其中的root为你希望将数据集下载到的地址，并且将download设置为True
train_dataset = datasets.MNIST(root = r'C:\Users\Administrator\Desktop\python\Pytorch和自然语言处理\多分类问题数据集',
                               train = True,
                               download=False,
                               transform=transform)
# 将数据集进行划分，之后一个一个batch进行读取并且训练
train_loader = DataLoader(train_dataset,
                          shuffle=True,
                          batch_size=batch_size)
test_dataset = datasets.MNIST(root = r'C:\Users\Administrator\Desktop\python\Pytorch和自然语言处理\多分类问题数据集',
                               train = False,
                               download=False,
                               transform=transform)
test_loader = DataLoader(train_dataset,
                          shuffle=False,
                          batch_size=batch_size)

全连接神经网络

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)

    def forward(self, x):
        kernel_size = x.view(-1, 784) # 将 (1*28*28)维度的张量的数据转换为 (1*784)维度的张量的数据
        # 使用relu作为激活函数
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return self.l5(x) # 最后一层网络不做激活，因为后期的损失函数选择了交叉熵损失，交叉熵损失会自动帮我们激活

实例化模型并且设置损失函数以及优化器

model = Net()
criterion = torch.nn.CrossEntropyLoss()
# lr即为学习率，momentum即为冲量大小
# momentum是为了尽量避免得到伪最优解
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

有关于momentum的具体解释可以看随机梯度下降优化算法、基于冲量的优化算法、TensorFlow中的优化算法API.

对训练集以及测试集进行训练

def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):
        inputs, target = data
        optimizer.zero_grad() # 将模型的参数梯度初始化为0
                              # 这一步非常重要，因为如果少了这一步，接下来每一次计算的参数梯度都会累加起来，这会导致整个结果出错
        outputs = model(inputs) # 前向传播计算预测值
        loss = criterion(outputs, target) # 计算当前的损失大小
        loss.backward() # 反向传播计算梯度
        optimizer.step() # 更新所有参数   

        running_loss += loss.item() # 为了防止我们的running_loss在计算图上，这里我们将loss.item()加给它
        if batch_idx % 300 == 299: # 每训练300次都打印出损失值进行查看
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))
            running_loss = 0.0

def test():
    correct = 0
    total = 0
    with torch.no_grad(): # 因为在测试集中我们不需要进行梯度计算，所以用了with torch.no_grad()
        for data in test_loader:
            images, labels = data
            outputs = model(images)
            # 因为我们预测出来的outputs为(64, 10)的概率矩阵，而我们需要的是该图片具体对应的一个数字
            # 所以我们取出每一行中概率最大的那个数字作为我们的预测结果
            _, predicted = torch.max(outputs.data, dim = 1) 
            correct += (predicted == labels).sum().item()# 计算出我们预测正确了的图片的数量
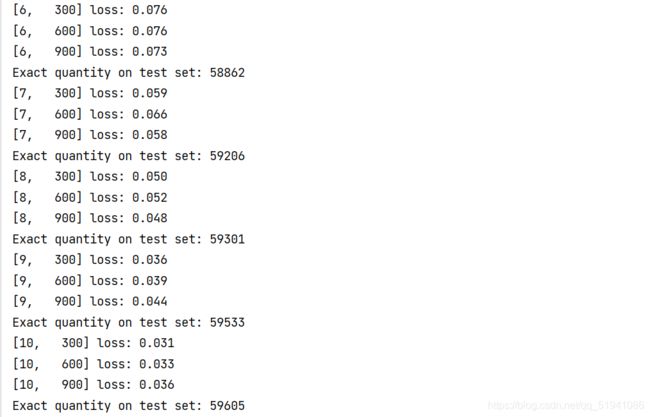
    print('Exact quantity on test set: %d' % correct)

由于我们在进行全连接神经网络训练的前向传播的时候是直接将x展开成了1*784的维度
例如下面这张图：

图片上所圈出的两个地方在图片上来看是非常接近的，都处于同一列，只是处于相邻两行
但是在将该图片的大小展开为了一维之后，这圈出来的两个点的距离就会变得比较大，所以这样数据就失去了原本存在的空间几何关系
但是使用卷积层神经网络就可以很好的减少这一点所带来的影响

使用卷积层神经网络

使用卷积层神经网络只需要将全连接神经网络中的模型换掉即可

定义卷积层神经网络模型

class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__() 
        # 进行卷积层训练
        self.conv1 = torch.nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = torch.nn.Conv2d(10, 20, kernel_size=5)
        # 进行池化层训练
        # 将维度(batch_size,10,24,24)转换为维度(batch_size,10,12,12)
        self.pooling = torch.nn.MaxPool2d(2)
        self.fc = torch.nn.Linear(320, 10)

    def forward(self, x):
        # 将 n*1*28*28维度的张量的数据转换为 n*784维度的张量的数据
        # 其中 n为样本的数量，也就是下面代码中的 batch_size
        batch_size = x.size(0)
        # 先将维度(batch_size,1,28,28)通过卷积层转换为维度(batch_size,10,24,24)
        # 再将维度(batch_size,10,24,24)通过池化层转换为维度(batch_size,10,12,12)
        x = F.relu(self.pooling(self.conv1(x)))
        # 先将维度(batch_size,10,12,12)通过卷积层转换为维度(batch_size,20,8,8)
        # 再将维度(batch_size,20,8,8)通过池化层转换为维度(batch_size,20,4,4)
        x = F.relu(self.pooling(self.conv2(x)))
        # 最后将维度(batch_size,20,4,4)展开成了维度(batch_size,320)
        x = x.view(batch_size, -1)
        x = self.fc(x)
        return x

接下来就是两种神经网络的训练结果的比较

全连接神经网络的训练结果：

卷积层神经网络的训练结果：

通过以上的结果可以看出卷积层神经网络要略优于全连接神经网络的训练结果