【改进灰狼优化算法】改进收敛因子和比例权重的灰狼优化算法【期刊论文完美复现】(Matlab代码实现)
欢迎来到本博客❤️❤️
博主优势:博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
本文目录如下:
目录
1 概述
2 运行结果
3 文献来源
4 Matlab代码实现
1 概述
文献来源:
摘要:在分析灰狼优化算法不足的基础上,提出一种改进的灰狼优化算法(CGWO),该算法采用基于余弦规律变化的收敛因子,平衡算法的全局搜索和局部搜索能力,同时引入基于步长欧氏距离的比例权重更新灰狼位置,从而加快算法的收敛速度。对8个经典测试函数进行仿真实验,结果表明CGWO算法的求解精度更高,稳定性更好。最后以预测谷氨酸菌体生长浓度为例,利用CGWO算法估计Richards模型的参数,以均方根误差和平均绝对误差作为评价指标,与PSO算法、GA算法和VS-FOA算法的结果进行比较,CGWO算法可以有效地估计Richards模型中的参数。
关键词:
灰狼优化算法;收敛因子;Richards模型;参数估计;
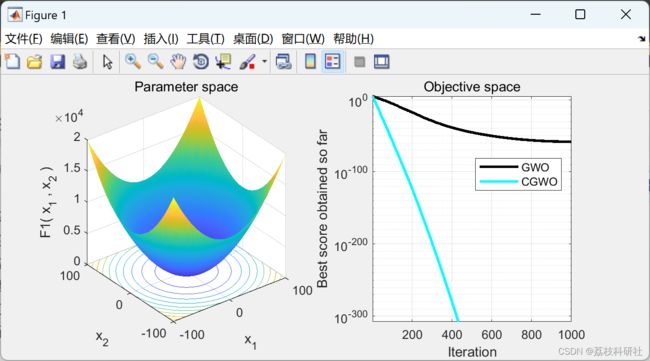
2 运行结果
部分代码:
function [Alpha_score,Alpha_pos,Convergence_curve]=CGWO(SearchAgents_no,Max_iter,lb,ub,dim,fobj)
%% 收敛因子参数
aintit = 2;
afinal = 0;
% initialize alpha, beta, and delta_pos
Alpha_pos=zeros(1,dim);
Alpha_score=inf; %change this to -inf for maximization problems
Beta_pos=zeros(1,dim);
Beta_score=inf; %change this to -inf for maximization problems
Delta_pos=zeros(1,dim);
Delta_score=inf; %change this to -inf for maximization problems
%Initialize the positions of search agents
Positions=initialization(SearchAgents_no,dim,ub,lb);
Convergence_curve=zeros(1,Max_iter);
l=0;% Loop counter
% Main loop
while l
% Return back the search agents that go beyond the boundaries of the search space
Flag4ub=Positions(i,:)>ub;
Flag4lb=Positions(i,:)
% Calculate objective function for each search agent
fitness=fobj(Positions(i,:));
% Update Alpha, Beta, and Delta
if fitness
Alpha_pos=Positions(i,:);
end
if fitness>Alpha_score && fitness
Beta_pos=Positions(i,:);
end
if fitness>Alpha_score && fitness>Beta_score && fitness
Delta_pos=Positions(i,:);
end
end
%% 改进点:收敛因子改进,文献中式(7)
n = 1;%递减系数
if(l<0.5*Max_iter)
a = afinal + (aintit - afinal)*(1 + (cos((l-1)*pi/( Max_iter-1)))^n)/2;
else
a = afinal + (aintit - afinal)*(1 - (cos((l-1)*pi/( Max_iter-1)))^n)/2;
end
% Update the Position of search agents including omegas
for i=1:size(Positions,1)
for j=1:size(Positions,2)
r1=rand(); % r1 is a random number in [0,1]
r2=rand(); % r2 is a random number in [0,1]
A1=2*a*r1-a; % Equation (3.3)
C1=2*r2; % Equation (3.4)
D_alpha=abs(C1*Alpha_pos(j)-Positions(i,j)); % Equation (3.5)-part 1
X1=Alpha_pos(j)-A1*D_alpha; % Equation (3.6)-part 1
r1=rand();
r2=rand();
A2=2*a*r1-a; % Equation (3.3)
C2=2*r2; % Equation (3.4)
D_beta=abs(C2*Beta_pos(j)-Positions(i,j)); % Equation (3.5)-part 2
X2=Beta_pos(j)-A2*D_beta; % Equation (3.6)-part 2
r1=rand();
r2=rand();
A3=2*a*r1-a; % Equation (3.3)
C3=2*r2; % Equation (3.4)
D_delta=abs(C3*Delta_pos(j)-Positions(i,j)); % Equation (3.5)-part 3
X3=Delta_pos(j)-A3*D_delta; % Equation (3.5)-part 3
%% 改进点:基于步长欧氏距离的比例权重
S = abs(X1) + abs(X2)+abs(X3);
if S~=0 %防止分母为0
W1 = abs(X1)/(abs(X1) + abs(X2)+abs(X3));
W2 = abs(X2)/(abs(X1) + abs(X2)+abs(X3));
W3 = abs(X3)/(abs(X1) + abs(X2)+abs(X3));
else
W1=1;W2=1;W3=1;
end
Positions(i,j)=(W1*X1+X2*W2+X3*W3)/3;% Equation (3.7)
end
end
l=l+1;
Convergence_curve(l)=Alpha_score;
end
3 文献来源
部分理论来源于网络,如有侵权请联系删除。
[1]王秋萍,王梦娜,王晓峰.改进收敛因子和比例权重的灰狼优化算法[J].计算机工程与应用,2019,55(21):60-65+98.