强化学习笔记:近端策略优化(PPO)
本文来自于datawhalechina的强化学习教程。
原文地址:https://datawhalechina.github.io/easy-rl/#/chapter5/chapter5
0x01 On-policy & Off-policy
在强化学习中,我们要让agent学习能够使得Q值尽可能大的策略。
- 如果做更新的策略和与环境互动的策略是同一个的话,称为On-policy;
- 如果不是同一个的话,称为Off-policy。
On-policy是比较麻烦的。我们以经典的策略梯度算法为例,每一次我们采集若干条轨迹 τ \tau τ 之后对agent做优化。但是这样有一个问题:我们每做一次优化,agent就不是原来的agent了。但是,我们采集的样本是基于原来的agent的,也就是说,之前采样了那么多轨迹,做了一次更新之后就直接没用了。
为了让之前采样到的数据能够多训练几次,我们可以使用重要性采样得到技术,确保一次采样后的数据可以多用几次。
0x02 重要性采样
假如我们有个函数 f ( X ) f(X) f(X) , X X X 是随机变量,我们来算一手 f ( X ) f(X) f(X) 的期望:
E f ( X ) = ∫ R f ( x ) p ( x ) d x Ef(X) = \int_R f(x) p(x) dx Ef(X)=∫Rf(x)p(x)dx
用蒙特卡洛法的话,我们会对X做若干采样,得到的样本 x i x_i xi 扔到 f f f 里求一手平均:
E f ( X ) ≈ 1 N ∑ i f ( x i ) Ef(X) \approx \frac 1 N \sum_{i} f(x_i) Ef(X)≈N1i∑f(xi)
但是我们没法从分布 p p p 里采样的话,我们可以从另一个分布 q q q 里做采样,然后做一下修正:
E f ( x ) = ∫ R f ( x ) p ( x ) d x = ∫ R f ( x ) p ( x ) q ( x ) q ( x ) d x = E q [ f ( x ) p ( x ) q ( x ) ] Ef(x) = \int_R f(x)p(x)dx = \int_R f(x)\frac{p(x)}{q(x)}q(x)dx = E_q[f(x)\frac{p(x)}{q(x)}] Ef(x)=∫Rf(x)p(x)dx=∫Rf(x)q(x)p(x)q(x)dx=Eq[f(x)q(x)p(x)]
上式意味着,我们从 q q q 里做采样的话,需要对采样的数据乘以重要性权重来修正两个分布的差异。
重要性采样有一些问题。虽然理论上你可以把 p p p 换成任何的 q q q。但是在实现上, p p p 和 q q q 不能差太多。
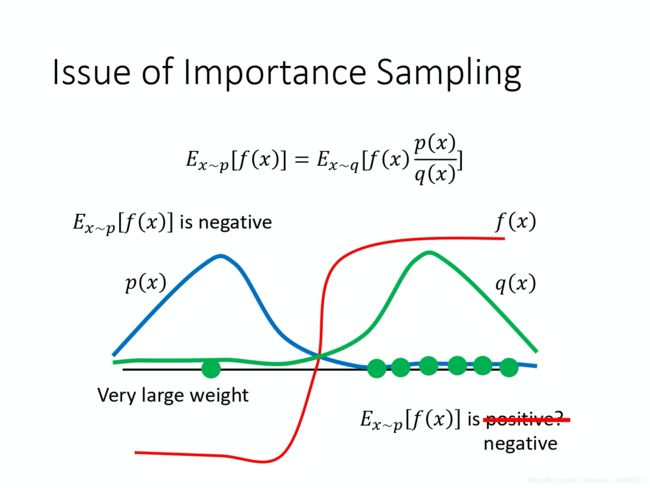
如上图,如果分布 p p p 和 q q q 差的太多,直接通过 p p p 求的期望是负的,但是如果 p p p 和 q q q 差太多,比如上图里,根据分布 q q q 修正之后求期望的结果可能就不好说了。假如采样太少,全采了右边的正数点,那么重要性采样求均值的结果就可能是正的。

我们现在要做的事情就是把重要性采样用在 off-policy 的情况,把 on-policy 训练的算法改成 off-policy 训练的算法。
现在,我们 τ \tau τ 是由agent θ ′ \theta' θ′ 采样出来的,然后真正作决策的agent θ \theta θ 会从这些 τ \tau τ 中学习更新自己的策略。

实际在做策略梯度的时候,我们并不是给整个轨迹 τ \tau τ 都一样的分数,而是每一个状态-动作的对(pair)会分开来计算。这个由马尔可夫性可以推导出来,此处不再赘述。
上图中, A A A 就是累计的奖励。我们先假设 A θ A^\theta Aθ 和 A θ ′ A^{\theta'} Aθ′的值差不多。然后,我们使用 θ ′ \theta' θ′ 的分布代替 θ \theta θ 的分布并且做一下修正。然后,我们假设模型是 θ \theta θ 和 θ ′ \theta' θ′ 的时候看到同一个状态的可能性是一样的,因此把他们约掉。
(理由如下:比如说玩不同的 Atari 的游戏,其实你看到的游戏画面都是差不多的,再者说这个东西确实很难算,有的时候一个 s t s_t st 根本不会出现第二次)
于是我们得到了一个损失函数 J θ ′ ( θ ) J^{\theta'}(\theta) Jθ′(θ)。对它做优化。 J θ ′ ( θ ) J^{\theta'}(\theta) Jθ′(θ) 的导数就是它上面一行的式子。
0x03 PPO
在搞重要性采样的时候我们不能让分布差得太多。因此,我们可以给分布之间的距离——KL散度加一个约束 δ \delta δ,这就是PPO的前身TRPO:
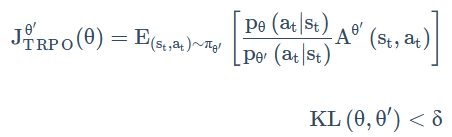
TRPO 是很难处理的,因为它把 KL 散度约束当做一个额外的约束,没有放目标(objective)里面,所以它很难算,所以一般就用 PPO 而不是 TRPO。看文献上的结果是,PPO 跟 TRPO 性能差不多,但 PPO 在实现上比 TRPO 容易的多。
PPO则是将KL散度作为一个正则项放到损失函数里做优化。
PPO算法还有两个主要的变种:PPO-penalty和PPO-clip。
首先来看PPO-penalty,也记为PPO-1。

在这个算法里,我们会先初始化一个策略的参数 θ 0 \theta_0 θ0 ,然后在每个迭代里,我们用 θ k \theta_k θk 和环境互动,生成一堆状态-动作对。
然后我们根据互动的结果估测一下 A θ k ( s t , a t ) A^{\theta_k}(s_t, a_t) Aθk(st,at) ,接着使用 PPO 的优化的公式。但跟原来的策略梯度不一样,原来的策略梯度只能更新一次参数,更新完以后就要重新采样数据。但是,现在我们可以让 θ \theta θ 更新很多次,因为由KL散度作为正则化项。
在 PPO 的论文里面还有一个 adaptive KL divergence。这边会遇到一个问题就是 β \beta β 要设多少,它就跟正则化一样。正则化前面也要乘一个权重,所以这个 KL 散度前面也要乘一个权重,但 β \beta β 要设多少呢?所以有个动态调整 β \beta β 的方法。
- 我们先设一个 β \beta β 的最大和最小值,作为容许界限。
- 如果优化一次之后,KL散度的项太大,则加大 β \beta β 的值。反之,如果KL散度的项太小,则减少 β \beta β 的值。
接着我们看PPO-clip,也记为PPO-2。
KL散度的计算可能很复杂,PPO-clip里面就没有KL散度。
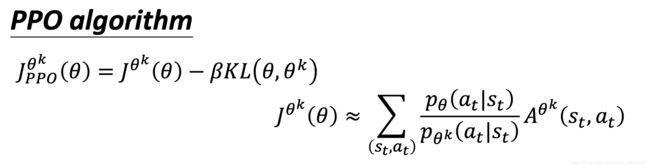
 这个 c l i p ( x , 1 − ϵ , 1 + ϵ ) clip(x, 1-\epsilon, 1 + \epsilon) clip(x,1−ϵ,1+ϵ) 函数的作用,就是当 x > 1 + ϵ x > 1 + \epsilon x>1+ϵ 的时候输出 1 + ϵ 1 + \epsilon 1+ϵ ,当 x < 1 − ϵ x < 1 - \epsilon x<1−ϵ 的时候输出 1 − ϵ 1 - \epsilon 1−ϵ,其他的时候不变。
这个 c l i p ( x , 1 − ϵ , 1 + ϵ ) clip(x, 1-\epsilon, 1 + \epsilon) clip(x,1−ϵ,1+ϵ) 函数的作用,就是当 x > 1 + ϵ x > 1 + \epsilon x>1+ϵ 的时候输出 1 + ϵ 1 + \epsilon 1+ϵ ,当 x < 1 − ϵ x < 1 - \epsilon x<1−ϵ 的时候输出 1 − ϵ 1 - \epsilon 1−ϵ,其他的时候不变。
也就是你拿来做示范的模型跟你实际上学习的模型,在优化以后不要差距太大。
比如说,A很大,我们要多增加对应的概率,但是不能增加太多,这个不能增加太多就由clip函数来体现:增加得过多的话,收益上也不会再增加。A很小,相应轨迹的出现概率则会减少,但是减得太厉害的话,比如小于 1 − ϵ 1 - \epsilon 1−ϵ ,也就不会再减少了。