机器学习实例（六）美国波士顿地区房价预测

回归问题预测的目标是连续变量

数据描述

# 从sklearn.datasets导入波士顿房价数据读取器
from sklearn.datasets import load_boston

# 从读取房价数据存储在变量boston中
boston = load_boston

# 输出数据描述
boston.DESCR

Number of Instances: 506
Number of Attributes: 13 numeric/categorical predictive.Median Value (attribute 14) is usually the target.
Missing Attribute Values: None
由上述可知，该数据集共有506条美国波士顿地区房价的数据，每条数据包括对指定房屋的13项数值型特征描述和目标房价（平均值）。另外，该数据中没有缺失的属性/特征值

数据处理

from sklearn.model_selection import train_test_split
import numpy as np

X = boston.data
y = boston.target

# 随机采样25%的数据构建测试样本，其余作为训练样本
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=33)

# 分析回归目标值的差异
print("The max target value is", np.max(boston.target))
print("The min target value is", np.min(boston.target))
print("The average target value is", np.mean(boston.target))

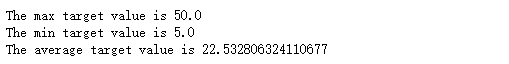
在上述对数据的探查中可以发现，预测目标房价之间的差异较大，因此需要对特征以及目标值进行标准化处理

# 从sklearn.preprocessing导入数据标准化模块
from sklearn.preprocessing import StandardScaler

# 分别初始化对特征和目标值的标准化器
ss_X = StandardScaler()
ss_y = StandardScaler()

# 分别对训练和测试数据的特征以及目标值进行标准化处理
X_train = ss_X.fit_transform(X_train)
X_test = ss_X.transform(X_test)
y_train = ss_y.fit_transform(y_train.reshape(-1,1))
y_test = ss_y.transform(y_test.reshape(-1,1))

标准化后的训练target集

标准化后的验证target集

尝试线性模型

这里尝试使用线性回归模型LinearRegression和SGDRegressor

# 从sklearn.linear_model导入LinearRegression
from sklearn.linear_model import LinearRegression

# 使用默认配置初始化线性回归器LinearRegression
lr = LinearRegression()

# 使用训练数据进行参数估计
lr.fit(X_train, y_train)

# 对测试数据进行回归预测
lr_y_predict = lr.predict(X_test)

# 从sklearn.linear_model导入SGDRegressor
from sklearn.linear_model import SGDRegressor

# 使用默认配置初始化线性回归器SGDRegressor
sgdr = SGDRegressor()

# 使用训练数据进行参数估计
sgdr.fit(X_train, y_train)

# 对测试数据进行回归预测
sgdr_y_predict = sgdr.predict(X_test)

线性模型评估

通过平均绝对误差、均方误差、R-squared评价模型
LinearRegression的评估

# 使用LinearRegression模型自带的评估模块，输出评估结果
print('The value of default measurement of LinearRegression is', lr.score(X_test, y_test))

# 从sklearn.metrics依次导入r2_score、mean_squared_error以及mean_absolute_error用于回归性能的评估
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error

# 使用r2_score模块,并输出评估结果
print('The value of R-squared of LinearRegression is', r2_score(y_test, lr_y_predict))

# 使用mean_squared_error模块,并输出评估结果
print('The mean squared error of LinearRegression is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)))

# 使用mean_absolute_error模块,并输出评估结果
print('The mean absolute error of LinearRegression is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(lr_y_predict)))

SGDRegressor的评估

# 使用SGDRegressor模型自带的评估模块，输出评估结果
print('The value of default measurement of SGDRegression is', sgdr.score(X_test, y_test))

# 从sklearn.metrics依次导入r2_score、mean_squared_error以及mean_absolute_error用于回归性能的评估
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error

# 使用r2_score模块,并输出评估结果
print('The value of R-squared of SGDRegressor is', r2_score(y_test, sgdr_y_predict))

# 使用mean_squared_error模块,并输出评估结果
print('The mean squared error of SGDRegressor is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(sgdr_y_predict)))

# 使用mean_absolute_error模块,并输出评估结果
print('The mean absolute error of SGDRegressor is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(sgdr_y_predict)))

可以看出模型自带的评分函数就是R-squared指标
SGDRegressor在面对训练数据规模十分庞大的任务时，可以在不损失过多性能的前提下，节省大量计算时间。根据Scikit-learn官网的建议，如果数据规模超过10万，推荐使用随机梯度法估计参数模型

尝试支持向量机模型

继续使用已经分割以及处理好的训练数据和测试数据
尝试三种不同核函数的支持向量机模型

# 从sklearn.svm中导入支持向量机(回归)模型
from sklearn.svm import SVR

# 使用线性核函数配置的支持向量机进行回归训练,并且对测试样本进行预测
linear_svr = SVR(kernel='linear')
linear_svr.fit(X_train, y_train)
linear_svr_y_predict = linear_svr.predict(X_test)

# 使用多项式核函数配置的支持向量机进行回归训练,并且对测试样本进行预测
poly_svr = SVR(kernel='poly')
poly_svr.fit(X_train, y_train)
poly_svr_y_predict = poly_svr.predict(X_test)

# 使用径向量核函数配置的支持向量机进行回归训练,并且对测试样本进行预测
rbf_svr = SVR(kernel='rbf')
rbf_svr.fit(X_train, y_train)
rbf_svr_y_predict = rbf_svr.predict(X_test)

模型评估

线性核函数支持向量机

# 从sklearn.metrics依次导入R-squared、MSE以及MAE用于回归性能的评估
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error

# 输出评估结果
print('R-squared value of linear SVR is', linear_svr.score(X_test, y_test))

# 使用mean_squared_error模块,并输出评估结果
print('The mean squared error of linear SVR is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(linear_svr_y_predict)))

# 使用mean_absolute_error模块,并输出评估结果
print('The mean absolute error of linear SVR is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(linear_svr_y_predict)))

多项式核函数支持向量机

# 输出评估结果
print('R-squared value of poly SVR is', poly_svr.score(X_test, y_test))

# 使用mean_squared_error模块,并输出评估结果
print('The mean squared error of poly SVR is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(poly_svr_y_predict)))

# 使用mean_absolute_error模块,并输出评估结果
print('The mean absolute error of poly SVR is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(poly_svr_y_predict)))

径向量核函数支持向量机

# 输出评估结果
print('R-squared value of rbf SVR is', rbf_svr.score(X_test, y_test))

# 使用mean_squared_error模块,并输出评估结果
print('The mean squared error of rbf SVR is', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(rbf_svr_y_predict)))

# 使用mean_absolute_error模块,并输出评估结果
print('The mean absolute error of rbf SVR is', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(rbf_svr_y_predict)))

尝试无参数模型

使用两种不同配置的K近邻回归模型

# 从sklearn.neighbors导入KNeighborRegressor
from sklearn.neighbors import KNeighborsRegressor

# 初始化K近邻回归器,并且调整配置,使得预测的方式为平均回归:weight='uniform'
uni_knr = KNeighborsRegressor(weights='uniform')
uni_knr.fit(X_train, y_train)
uni_knr_y_predict = uni_knr.predict(X_test)

# 初始化K近邻回归器,并且调整配置,使得预测的方式为平均回归:weight='distance'
dis_knr = KNeighborsRegressor(weights='distance')
dis_knr.fit(X_train, y_train)
dis_knr_y_predict = dis_knr.predict(X_test)

无参数模型评估

平均回归K近邻模型

# 使用R-squared.MSE以及MAE三种指标对平均回归配置的K近邻模型在测试集上进行性能评估
print('R-squared value of uniform-weighted KNeighborRegression:', uni_knr.score(X_test, y_test))
print('The mean squared error of uniform-weighted KNeighborRegression:', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(uni_knr_y_predict)))
print('The mean absoluate error of uniform-weighted KNeighborRegression:', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(uni_knr_y_predict)))

距离加权回归K近邻模型

# 使用R-squared、MSE以及MAE三种指标对根据距离加权回归配置的K近邻模型在测试集上进行性能评估
print('R-squared value of distance-weighted KNeighborRegression:', dis_knr.score(X_test, y_test))
print('The mean squared error of distance-weighted KNeighborRegression:', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(dis_knr_y_predict)))
print('The mean absoluate error of distance-weighted KNeighborRegression:', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(dis_knr_y_predict)))

尝试回归树模型

回归树的叶节点返回的是“一团”训练数据的均值，而不是具体的、连续的预测值

# 从sklearn.tree中导入DecisionTreeRegressor
from sklearn.tree import DecisionTreeRegressor

# 使用默认配置初始化DecisionTreeRegressor
dtr = DecisionTreeRegressor()

# 用波士顿房价的训练数据构建回归树
dtf.fit(X_train, y_train)

# 使用默认配置的单一回归树对测试数据进行预测,并将预测值存储在变量dtr_y_predict中
dtr_y_predict = dtr.predict(X_test)

回归树模型评估

# 使用R-squared、MSE以及MAE指标对默认配置的回归树在测试集上进行性能评估
print('R-squared value of DecisionTreeRegressor:', dtr.score(X_test, y_test))
print('The mean squared error of DecisionTreeRegressor:', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(dtr_y_predict)))
print('The mean absolute error of DecisionTreeRegressor:', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(dtr_y_predict)))

特点分析

• 树模型可以解决非线性特征的问题
• 树模型不要求对特征标准化和统一量化，即数值型和类别型特征都可以直接被应用在树模型的构建和预测过程中
• 树模型也可以直观地输出决策过程，使得预测结果具有可解释性

同时，树模型也有一些显著的缺陷

• 正是因为树模型可以解决复杂的非线性拟合问题，所以更加容易因为模型搭建过于复杂而丧失对新数据预测的精度
• 树模型从上至下的预测流程会因为数据细微的更改而发生较大的结构变化，因此预测稳定性较差
• 依托训练数据构建最佳的树模型是NP难问题，即在有限时间内无法找到最优解的问题，因此我们所使用类似贪婪算法的解法只能找到一些次优解，这也是为什么我们经常借助集成模型，在多个次优解中寻觅更高的模型性能

尝试集成模型

极端随机森林，与普通的随机森林模型不同的是，极端随机森林在每当构建一棵树的分裂节点的时候，不会任意地选取特征；而是先随机收集一部分特征，然后利用信息熵和基尼不纯性等指标挑选最佳的节点特征
尝试了RandomForestRegressor、ExtraTreesRegressor以及GradientBoostingRegressor三种模型

# 从sklearn.ensemble中导入RandomForestRegressor、ExtraTreesGressor以及GradientBoostingRegressor
from sklearn.ensemble import RandomForestRegressor, ExtraTreesRegressor, GradientBoostingRegressor
# 使用RandomForestRegressor训练模型,并对测试数据做出预测,结果存储在变量rfr_y_predict中
rfr = RandomForestRegressor()
rfr.fit(X_train, y_train)
rfr_y_predict = rfr.predict(X_test)

# 使用ExtraTreesRegressor训练模型,并对测试数据做出预测,结果存储在变量etr_y_predict中
etr = ExtraTreesRegressor()
etr.fit(X_train, y_train)
etr_y_predict = etr.predict(X_test)

# 使用GradientBoostingRegressor训练模型,并对测试数据做出预测,结果存储在变量gbr_y_predict中
gbr = GradientBoostingRegressor()
gbr.fit(X_train, y_train)
gbr_y_predict = gbr.predict(X_test)

集成模型评估

随机回归森林

# 使用R-squared.MSE以及MAE指标对默认配置的随即回归森林在测试集上进行性能评估
print('R-squared value of RandomForestRegressor:', rfr.score(X_test, y_test))
print('The mean squared error of RandomForestRegressor:', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(rfr_y_predict)))
print('The mean absoluate error of RandomForestRegressor:', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(rfr_y_predict)))

极端回归森林

# 使用R-squared.MSE以及MAE指标对默认配置的极端回归森林在测试集上进行性能评估
print('R-squared value of ExtraTreesRegressor:', etr.score(X_test, y_test))
print('The mean squared error of ExtraTreesRegressor:', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(etr_y_predict)))
print('The mean absoluate error of ExtraTreesRegressor:', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(etr_y_predict)))

# 使用训练好的极端回归森林模型,输出每种特征对预测目标的贡献度
print(np.sort(list(zip(etr.feature_importances_, boston.feature_names)), axis=0))

梯度回归森林

# 使用R-squared.MSE以及MAE指标对默认配置的梯度上升回归森林在测试集上进行性能评估
print('R-squared value of GrandientBoostingRegressor:', gbr.score(X_test, y_test))
print('The mean squared error of GrandientBoostingRegressor:', mean_squared_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(gbr_y_predict)))
print('The mean absoluate error of GrandientBoostingRegressor:', mean_absolute_error(ss_y.inverse_transform(y_test), ss_y.inverse_transform(gbr_y_predict)))

不难看出，集成模型往往可以提供更高的表现性能和更好的稳定性