基于柯西变异的蚁狮优化算法 - 附代码
基于柯西变异的蚁狮优化算法
文章目录
- 基于柯西变异的蚁狮优化算法
-
- 1.蚁狮优化算法
- 2. 改进蚁狮优化算法
-
- 2.1 基于柯西变异算子改进
- 3.实验结果
- 4.参考文献
- 5.Matlab代码
- 6.Python代码
摘要:针对蚁狮优化算法较易陷入局部最优停滞,收敛精度低以及收敛速度较慢等问题,将自适应t分布的柯西变异融入到蚁狮优化算法中,提出了基于柯西变异的蚁狮优化算法(CALO).该算法采用随机的方法挑选出精英蚁狮个体,改善蚁狮群体的适应性,提高种群的总体寻优效率;采用具有自适应的柯西变异算子使得蚁狮个体受局部极值点约束力下降,能够快速跳出局部最优,大大提高了全局搜索能力和收敛速度;
1.蚁狮优化算法
基础蚁狮优化算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107726004
2. 改进蚁狮优化算法
2.1 基于柯西变异算子改进
针对蚁狮算法的不足,进一步提出了基于柯西变异的蚁狮优化算法 .柯西高斯变异算子可以很大程度上提高算法全局勘探能力, 收敛精度以及稳定度. 比如近年来 柯西累积分布改进的鲸鱼优化算法, 柯西变异策略改进的果蝇算法均得到了良好的优化效果.
柯西分布如下:
s = t π ( x 2 + t 2 ) , − ∞ < x < + ∞ s=\frac{t}{\pi\left(x^{2}+t^{2}\right)}, \quad-\infty
柯西分布从峰值向两侧下降相对平缓, 蚁狮个体受局部的极值点约束力在柯西变异后下降, 并且 柯西分布的峰值相对较小, 蚁狮在变异后会花费相 对较少的时间来搜索相邻区间, 把更多的时间放在 掜寻全局最优值上, 使得改进的蚁狮优化算法在寻 找全局的最优值方面具有很好的调节能力. 利用上述柯西分布特点对蚁狮优化算法进行优化改进, 在 精英蚁狮个体的状态上引入服从柯西分布的随机向 量,公式如下:
x ′ = x + η Cauch y ( 0 , 1 ) x^{\prime}=x+\eta \text { Cauch } y(0,1) x′=x+η Cauch y(0,1)
式中, x ′ x^{\prime} x′ 为初始位置 x x x 的更新位置; Cauchy ( 0 , 1 ) (0,1) (0,1) 是 t = 1 t=1 t=1 时的标准柯西随机分布; 参数 η \eta η 是用来控制柯西分布变异强度的一个常数.
基于柯西变异的蚁狮优化算法的步㵵为:
步骤 1:执行原基本蚁狮优化算法的步骤 1 ∼ 1 \sim 1∼ 步骤 4 ;
步骤 2 : 在进入循环迭代后, 当䖢狮群体中相邻 两次迭代的几乎没有差别的最优值都作为历史最优 值被记录下来时, 我们认为算法陷入局部最优停滞, 此时需要进行柯西变异;
步骤 3:变异操作: 先将最优蚁狮个体的适应值 和个数复制到原先种群的规模, 然后嵌入柯西变异 算子, 进一步更新蚊狮群体的位置, 并更新最优值.
A 0 ′ = A 0 + A 0 ∗ Cauchy ( 0 , 1 ) A L 0 ∘ = A L 0 + A L 0 ∗ Cauch y ( 0 , 1 ) \begin{aligned} &A_{0}{ }^{\prime}=A_{0}+A_{0} * \text { Cauchy }(0,1) \\ &A L_{0}{ }^{\circ}=A L_{0}+A L_{0} * \operatorname{Cauch} y(0,1) \end{aligned} A0′=A0+A0∗ Cauchy (0,1)AL0∘=AL0+AL0∗Cauchy(0,1)
式中, A 0 , A L 0 A_{0}, A L_{0} A0,AL0 是原蚁狮和蚂蚁个体的初始位置; A 0 , A L 0 A_{0}, A L_{0} A0,AL0 '是经过柯西变异操作后更新的新位置.
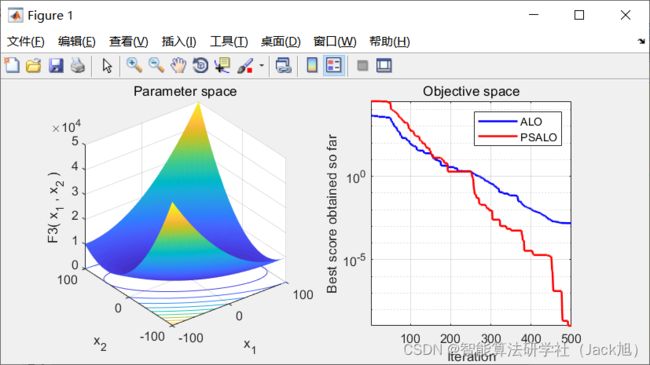
3.实验结果
4.参考文献
[1]于建芳,刘升,韩斐斐,肖子雅.基于柯西变异的蚁狮优化算法[J].微电子学与计算机,2019,36(06):45-49+54.