小生镜粒子群优化算法-附代码

小生镜粒子群优化算法-附代码

摘要：针对粒子群算法容易早熟收敛和后期收敛速度慢的缺点, 结合进化论中小生境技术, 提出了小生境粒子群优化算法。通过粒子之间的距离找到具有相似距离的粒子个体组成小生境种群, 然后在该种群里面利用粒子群优化算法进化粒子, 所有个体经过其小生境群体的进化之后, 找到最优的个体存入到下一代的粒子群中, 直到找到满意的适应值为止。

1.粒子群优化算法

基础粒子群算法的具体原理参考网络博客
$$\begin{array}{rl}& {\mathrm{v}}_{\mathrm{id}}(\mathrm{t}+1)={\omega }^{\ast }{\mathrm{v}}_{\mathrm{id}}(\mathrm{t})+{\alpha }^{\ast }\mathrm{rand}({)}^{\ast }\left({\mathrm{p}}_{\mathrm{i},\mathrm{d}}-{\mathrm{x}}_{\mathrm{id}}(\mathrm{t})\right)+{\beta }^{\ast }\mathrm{rand}()\ast \left({\mathrm{p}}_{\mathrm{g},\mathrm{d}}{\mathrm{x}}_{\mathrm{id}}(\mathrm{t})\right)(1)\\ & {\mathrm{x}}_{\mathrm{id}}(\mathrm{t}+1)={\mathrm{x}}_{\mathrm{id}}(\mathrm{t})+{\mathrm{v}}_{\mathrm{id}}(\mathrm{t}+1)(2)\end{array}$$

2. 小生镜粒子群优化算法

进化论中小生境概念指生物在特定环境下的生存环境 这 概念的主要思想是 “以群分, 物以类聚”, 即反映了在大自然 的进化过程中, 各种生物在特定环境下生存, 同种生物中存在 着优秀的生物, 各生物之间存在着相互竞争, 不同种生物之间 又存在着信息交换。资源共享”体现了在特定环境中共同生存 的同种生物分享有限的资源, 这些生物之间通过相互协调达到 共同进化, 对于适应环境能力弱的生物, 在资源不足的前提下, 将会逐渐被淘汰 。
在小生境粒子群算法中, 主要分为两个阶段, 第一个阶段 由小生境技术根据粒子之间矩离找到每个粒子的小生境群体, 然后在每个小生境群体中利用粒子群算法进行速度和位置更 新, 其中粒子群的群体最优值仅在该小生境群体中起作用。对 于更新后的群体, 根据粒子间的距离, 利用共享机制提高粒子 的适应度, 对于适应度最低的个体, 利用罚函数进行处罚相应的 粒子。最后保留每个粒子的群体最优个体, 直到满足终止条件。
(1) 小生境群体的划分
对于粒子 ${\mathrm{X}}_{\mathrm{i}}=\left({\mathrm{x}}_{\mathrm{i}},{\mathrm{x}}_{\mathrm{i}},\cdots ,{\mathrm{x}}_{\mathrm{im}}\right),\mathrm{i}=1,2,\cdots ,\mathrm{N}$, 它的小生境群 体是计算该粒子与其他粒子之间的范数。
$${\mathrm{d}}_{\mathrm{ik}}=\Vert {\mathrm{X}}_{\mathrm{i}}-{\mathrm{X}}_{\mathrm{k}}\Vert ,\mathrm{k}=1,2,\cdots ,\mathrm{N}\text{\hspace{1em}(3)}$$
对于给定参数 ${\sigma }_0$, 如果 ${\mathrm{d}}_{\mathrm{k}}<{\sigma }_0,\mathrm{k}=1,2,\cdots ,\mathrm{N}$, 则该个体加 入到该小生境群体 ${\mathrm{X}}_{\mathrm{p},}$, 这里范数一般对于实值函数取为欧式 距离

(2) 粒子之间的共享函数

粒子 $\mathrm{i}$ 和粒子 $\mathrm{j}$ 之间的共享函数为:
$${\mathrm{Shd}}_{\mathrm{ij}}=\{\begin{array}{cc}1& {\mathrm{d}}_{\mathrm{ij}}=0\\ 1-{\left(\frac{{\mathrm{d}}_{\mathrm{ij}}}{{\sigma }_0}\right)}^{\lambda }& {\mathrm{d}}_{\mathrm{ij}}<{\sigma }_0\\ 0& \text{ 否则 }\end{array}\text{\hspace{1em}(4)}$$
$\lambda$ 为控制共享函数形状的参数。
(3) 适应值函数的更新 根据共享机制函数更新该粒子的适应值：
$$f_j^{\prime }=\frac{f_j}{m}\text{\hspace{1em}(5)}$$ { }
其中 $m={\sum }_{s=i}^{i+p-1}{S}_j{h}_{js},j=i,i+1,\cdots ,i+p_i-1(6)$

具体的算法流程:
步骤 1 初始化粒子群体为 $\mathrm{X}=\left\{{\mathrm{X}}_1,{\mathrm{X}}_2,\cdots ,{\mathrm{X}}_{\mathrm{N}}\right\}$, 其中每个粒 子个体为 $X_i=\left(x_1,x_2,\cdots ,x_m\right),i=1,2,\cdots ,N$;
步骤 2 按下列步骤确定小生境种群个体:
(2.1) 置 $\mathrm{i}=1$;
(2.2) 计算两个粒子个体的距离按照式(3) 计算;
(2.3) 根据 ${\mathrm{d}}_{\mathrm{ik}}<{\sigma }_0,\mathrm{k}=\mathrm{i},\mathrm{i}+1,\cdots ,\mathrm{N}$, 确定小生境子群 ${\mathrm{X}}_{{\mathrm{p}}_{\mathrm{i}}},{\mathrm{p}}_{\mathrm{i}}$ 为 ${\mathrm{X}}_{{\mathrm{p}}_{\mathrm{i}}}$ 的元素个数, 其中 ${\sigma }_0$ 依据问题(NFP) 而定;
步骤 3 按照粒子群算法对小生境群体进行速度和适应度 更新：
(3.1) 设置加速常数 $\alpha$ 和 $\beta$, 最大进化代数 ${\mathrm{T}}_{p_1}$, 当前进化代 数置为 $\mathrm{T}=1$, 并且每初始化每个粒子的速度, 其粒子初始最优 位置为粒子自身;
(3.2) 按照方程 (1) 和 (2) 进行粒子位置和速度更新。其中 群体最优值为小生境群体的最优值, 不再是整个群体的最优值;
(3.3) 检查条件, 对于更新后的个体 ${\mathrm{X}}_{{\mathrm{p}}_{\mathrm{i}}}{}^{\prime }$, 按照式(5) 对 ${\mathrm{X}}_{{\mathrm{p}}_{\mathrm{i}}}$ 中的第 $\mathrm{j}$ 个粒子进行速度和位置更新个体的更新适应度;
(3.4) 利用更新适应度 ${\mathrm{f}}_{\mathrm{j}}^{\prime }$ 及处罚函数 Penalty 对该子群中 低适应度的粒子进行处罚, 即当 ${\mathrm{x}}_{\mathrm{j}},{\mathrm{x}}_{\mathrm{k}}\in {\mathrm{M}}_{{\mathrm{p}}_{\mathrm{i}}},\Vert {\mathrm{x}}_{\mathrm{j}}-{\mathrm{x}}_{\mathrm{k}}||<\mathrm{L},\mathrm{L}<\sigma$ 时, 比较两个粒子的距离, 并对其中适应度较低的粒子进行处罚：
$${\mathrm{f}}_{\min }\left({\mathrm{x}}_{\mathrm{j}},{\mathrm{x}}_{\mathrm{k}}\right)=\text{ Penalty, }\mathrm{j},\mathrm{k}=\mathrm{i},\mathrm{i}+1,\cdots ,\mathrm{i}+{\mathrm{p}}_{\mathrm{i}}-1$$
(3.5) 当 $i+p_i<N$ 时, 置 $i\leftarrow i+p_i$, 返回步骤 (3.2); 否则, 进入 下一步;
步骤 4 计算每个粒子的适应值, 保留最优的适应值和个 体, 检查是否达到优化条件, 如果达到误差精度, 则结束。否则, 然后进入下一个粒子的小生境群体进行优化;

步骤 5 若没有找到最优值, 则对每个粒子的小生境群体 保留的最优个体组成新的群体空间, 重复步骤 2。
以上算法通过利用粒子间的距离划分每个粒子的小生境 群体, 然后在小生境群体内利用粒子群算法的进化机理对群体 内的每个粒子进行更新。对于更新后的群体, 利用共享机制算 法对适应值进行更新, 对于适应度最低的粒子利用处罚函数进 行处罚。

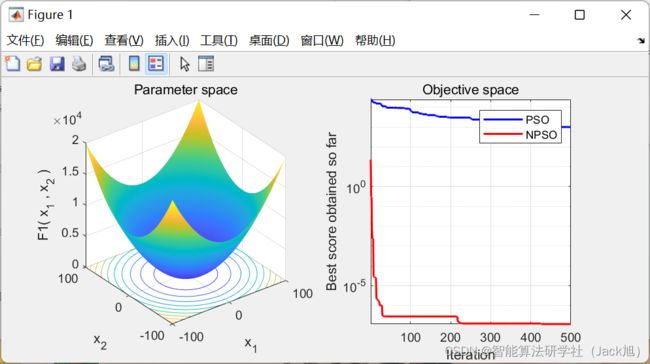
3.实验结果

4.参考文献

[1]向长城,黄席樾,杨祖元,杨欣.小生境粒子群优化算法[J].计算机工程与应用,2007(15):41-43.

5.Matlab代码

6.Python代码