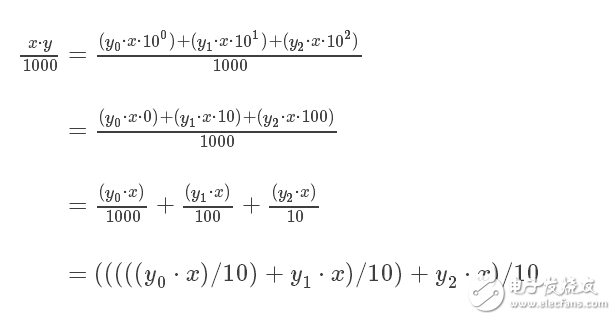用c语言实现蒙哥马利算法,蒙哥马利算法的概念与原理 - 全文
蒙哥马利(Montgomery)幂模运算是快速计算a^b%k的一种算法,是RSA加密算法的核心之一。
蒙哥马利模乘的优点在于减少了取模的次数(在大数的条件下)以及简化了除法的复杂度(在2的k次幂的进制下除法仅需要进行左移操作)。模幂运算是RSA 的核心算法,最直接地决定了RSA 算法的性能。
针对快速模幂运算这一课题,西方现代数学家提出了大量的解决方案,通常都是先将幂模运算转化为乘模运算。
这里为大家梳理一下整个蒙哥马利算法的本质,蒙哥马利算法并不是一个独立的算法,而是三个相互独立又相互联系的算法集合,其中包括
蒙哥马利乘模,是用来计算x⋅y (mod N)
蒙哥马利约减,是用来计算t⋅ρ−1 (mod N)
蒙哥马利幂模,是用来计算xy (mod N)
其中蒙哥马利幂乘是RSA加密算法的核心部分。
基本概念
梳理几个概念,试想一个集合是整数模N之后得到的
ZN={0,1,2,⋯,N−1}
注:N在base-b进制下有lN位。 比如10进制和100进制,都属于base-10进制,因为100=102,所以b=10。在10进制下,667的lN=3这样的集合叫做N的剩余类环,任何属于这个集合Z的x满足以下两个条件:
1. 正整数
2. 最大长度是lN
文中讲到的蒙哥马利算法就是用来计算基于ZN集合上的运算,简单讲一下原因,因为RSA是基于大数运算的,通常是1024bit或2018bit,而我们的计算机不可能存储完整的大数,因为占空间太大,而且也没必要。因此,这种基于大数运算的加密体系在计算的时候都是基于ZN集合的,自然,蒙哥马利算法也是基于ZN。
在剩余类环上,有两种重要的运算,一类是简单运算,也就是加法和减法,另一类复杂运算,也就是乘法。我们比较熟悉的是自然数集上的运算,下面看下怎么从自然数集的运算演变成剩余类环上的运算。
对于加法运算,如果计算x±y (mod N) (0≤x,y<N),试想自然数集上的 x±y
0≤x+y≤2⋅(N−1)
−(N−1)≤x−y≤(N−1)我们可以简单的通过加减N来实现从自然数到剩余类集的转换
另外一类是乘法操作,也就是x⋅y (mod N)(0≤x,y<N),那么
0≤x⋅y≤(N−1)2如果在自然数集下,令t=x⋅y,那么对于modN我们需要计算
t−(N⋅⌊t/N⌋)加减操作很简单,具体的算这里就不细说了,我们用ZN−ADD 来代表剩余类环上的加法操作。既然我们可以做加法操作,那么我们就可以扩展到乘法操作,算法如下
但是这并不是一个好的解决方案,因为通常来说,我们不会直接做w位乘w位的操作,这个后面会用蒙哥马利的乘法来代替解决。
对于取模操作,一般有以下几种方法
1,根据以下公式,来计算取模操作
t−(N⋅⌊t/N⌋)
这种解法有以下特征
整个计算过程是基于标准的数字表示
不需要预计算(也就是提前计算一些变量,以备使用)
涉及到一个除法操作,非常费时和复杂
2,用Barrett reducTIon算法,这篇文章不细说,但是有以下特征
基于标准的数字表示
不需要预计算
需要2⋅(lN+1)⋅(lN+1) 次数乘运算
3,用蒙哥马利约减,也就是下面要讲的算法,有以下特征
不是基于标准的数字表示(后文中有提到,是基于蒙哥马利表示法)
需要预计算
需要2⋅(lN)⋅(lN) 次数乘运算
蒙哥马利预备知识
在将蒙哥马利算法之前,先看一下在自然数下的乘法公式
计算x⋅y,想象一下我们常用的计算乘法的方法,用乘数的每一位乘上被乘数,然后把得到的结果相加,总结成公式,可以写成如下的形式。
x⋅y=x⋅sumly−1i=0yi⋅bi
=sumly−1i=0yi⋅x⋅bi
尝试下面一个例子,10进制下(也就是b=10),y=456(也就是ln=3),计算x⋅y,公式可演变如下:
x⋅y=(y0⋅x⋅100)+(y1⋅x⋅101)+(y2⋅x⋅102)
=(y0⋅x⋅0)+(y1⋅x⋅10)+(y2⋅x⋅100)
=(y0⋅x)+10⋅(y1⋅x+10⋅(y2⋅x⋅+10⋅(0)))
最后一次演变其实就是用霍纳法则(Horner’s rule)所讲的规则,关于霍纳法则,可以自行百度。
这个计算过程写成代码实现的算法应该是这样的:
接下来我们来看下面这样的计算,计算(x⋅y)/1000,由前面可以知道
x⋅y=(y_0⋅x)+10⋅(y_1⋅x+10⋅(y_2⋅x⋅+10⋅(0)))
由此可以知道:
这个计算过程写成代码实现的算法是这样的:
接下来我们再来看在剩余类集合下的乘法操作 x⋅y/1000 (mod 667)
我们知道剩余类集合Z667={0,1⋯666},是不存在小数的,而如果我们采用自然数集的计算方式的话,就会出现小数,比如前面的例子,除10就会有小数。
这个问题是这样的,我们知道u⋅667≡0(mod667)(≡表示取模相等),所以我们可以选择一个合适的u,用u乘667再加上r,使得和是一个可以除10没有小数,这样在mod 667之后依然是正确的结果。至于u怎么算出来,这篇文章会在后面的章节说明。
这个过程之后x⋅y/1000 (mod 667) 的计算算法可以写成如下的形式
至此,你可能还不明白上面说这一堆演变的原因,其实很简单,原来是一个(x⋅y) (mod 667)的运算,这个运算中的模操作,正常情况下是要通过除法实现的,而除法是一个特别复杂的运算,要涉及到很多乘法,所以在大数运算时,我们要尽量避免除法的出现。而通过以上几个步骤,我们发现(x⋅y)/1000 (mod 667)这个操作是不用除法的。等等,算法中明明有个除10的操作,你骗谁呢。不知道你有没有发现,除数其实是我们的进制数,除进制数在计算机中是怎么做呢,其实很简单,左移操作就ok了。所以这个计算方法是不涉及到除法操作的。
但是我们要计算的明明是(x1⋅y1) (mod 667),怎么现在变成了(x2⋅y2)/1000 (mod 667),所以在下一步,我们要思考的是怎么样让(x1⋅y1) (mod 667)转变成(x2⋅y2)/1000 (mod 667)这种形式。
考虑这样两个算法
- 第一个是输入x和y,计算x⋅y⋅ρ−1
-第二个算法,输入一个t,计算t⋅ρ−1。
x⋅y (mod 667)=((x⋅1000)⋅(y⋅1000)/1000)/1000 (mod 667)
是不是变成了我们需要的(x⋅y)/1000 (mod 667)模式,而且这个转变过程是不是可以通过上面两个算法来实现,输入值如果是(x⋅1000)和(y⋅1000),则通过第一个算法可以得到((x⋅1000)⋅(y⋅1000)/1000),把结果作为第二个算法的输入值,则通过第二个算法可以得到((x⋅1000)⋅(y⋅1000)/1000)/1000。
算法的详解
扯了一大顿,终于引出了今天文章的主角,前面讲到的两个算法,第一个就是蒙哥马利乘模,第二个就是蒙哥马利约减。下面我们来讲这两个算法的详解。
正如前面提到的蒙哥马利算法的三个特性之一是,不是基于普通的整数表示法,而是基于蒙哥马利表示法。什么是蒙哥马利表示法呢,其实也很简单,上面我们提到,要让(x1⋅y1) (mod 667)转变成(x2⋅y2)/1000 (mod 667)这种形式,我们需要将输入参数变成(x⋅1000)和(y⋅1000),而不是x和y本身,而(x⋅1000)和(y⋅1000) 其实就是蒙哥马利表示法。
所以我们先定义几个概念:
蒙哥马利参数
给定一个N,N在b进制(例如,二进制时,b=2)下共有l位,gcd(N,b)=1,先预计算以下几个值(这就是前面提到的特性之一,需要预计算):
ρ=bk 指定一个最小的k,使得bk》N
ω=−N−1(mod ρ)
这两个参数是做什么用的呢,你对照前面的演变过程可以猜到ρ 就是前面演变中的1000,而ω 则是用来计算前面提到的u的。
蒙哥马利表示法
对于x,0≤x≤N−1,x的蒙哥马利表示法表示为x=x⋅ρ (mod N)
蒙哥马利约减
蒙哥马利约减的定义如下
给定一些整数t,蒙哥马利约减的计算结果是t⋅ρ−1 (mod N)
蒙哥马利约减的算法可表示为
蒙哥马利约减可以算作是下面要说的蒙哥马利模乘当x=1时的一种特殊形式,。同时它又是蒙哥马利乘模要用到的一部分,这在下一部分讲蒙哥马利乘模的时候有讲到。
蒙哥马利约减可以用来计算某个值得取模操作,比如我们要计算m(mod N),只需要将m
的蒙哥马利表示法m⋅ρ作为参数,带入蒙哥马利约减,则计算结果就是m(mod N)。
蒙哥马利乘模
一个蒙哥马利乘模包括整数乘法和蒙哥马利约减,现在我们有蒙哥马利表示法:
x^=x⋅ρ (mod N)
y^=y⋅ρ (mod N)
它们相乘的结果是
t=x^⋅y^
=(x⋅ρ)⋅(y⋅ρ)
=(x⋅y)⋅ρ2
最后,用一次蒙哥马利约减得到结果
t^=(x⋅y)⋅ρ (mod N)
上面我们可以看出,给出的输入参数是x^ 和y^, 得到的结果是(x⋅y)⋅ρ (mod N),所以蒙哥马利乘法也可以写成如下形式,已知输入参数x和y,蒙哥马利乘法是计算(x⋅y)⋅ρ−1 (mod N)
举个例子:
b=10,也就是说在10进制下,N=667
让bk》N的最小的k是3,所以ρ=bk=103=1000
ω=−N−1 (mod ρ)=−667−1 (mod ρ)=997
因为x=421,所以x^=x⋅ρ(mod N)=421⋅1000(mod 667)=123
因为y=422,所以y^=y⋅ρ(mod N)=422⋅1000(mod 667)=456
所以计算x^和y^蒙哥马利乘结果是
x^⋅y^⋅ρ−1=(421⋅1000⋅422⋅1000)⋅1000−1 (mod 667)
(421⋅422)⋅1000 (mod 667)
(240)⋅1000 (mod 667)
547 (mod 667)
然后总结一下蒙哥马利约减和蒙哥马利乘法的伪代码实现,这个算法其实就是从蒙哥马利预备知识讲到的算法演变来的。
上面的例子用这个算法可以描述为
蒙哥马利算法是一套很完美的算法,为什么这么说呢,你看一开始已知x,我们要求x^=x⋅ρ,这个过程可以通过蒙哥马利乘法本身来计算,输入参数x和ρ2,计算结果就是x^=x⋅ρ。然后在最后,我们知道x^=x⋅ρ,要求得x的时候,同样可以通过蒙哥马利算法本身计算,输入参数x^和1,计算结果就是x。有没有一种因就是果,果就是因的感觉,这就是为什么说蒙哥马利算法是一套很完美的算法。
蒙哥马利幂模
最后,才说到我们最开始提到的RSA的核心幂模运算,先来看一下普通幂运算的算法是怎么得出来的。
以下资料来自于百度百科快速模幂运算
针对快速模幂运算这一课题,西方现代数学家提出了大量的解决方案,通常都是先将幂模运算转化为乘模运算。
例如求D=C^15%N
由于:a*b % n = (a % n)*(b % n) % n
所以令:
C1 =C*C % N =C^2 % N
C2 =C1*C % N =C^3 % N
C3 =C2*C2 % N =C^6 % N
C4 =C3*C % N =C^7 % N
C5 =C4*C4 % N =C^14 % N
C6 =C5*C % N =C^15 % N
即:对于E=15的幂模运算可分解为6 个乘模运算,归纳分析以上方法可以发现:
对于任意指数E,都可采用以下算法计算D=C**E % N:
D=1
WHILE E》0
IF E%2=0
C=C*C % N
E=E/2
ELSE
D=D*C % N
E=E-1
RETURN D
继续分析会发现,要知道E 何时能整除 2,并不需要反复进行减一或除二的操作,只需验证E 的二进制各位是0 还是1 就可以了,从左至右或从右至左验证都可以,从左至右会更简洁,
设E=Sum[i=0 to n](E*2**i),0《=E《=1
则:
D=1
FOR i=n TO 0
D=D*D % N
IF E=1
D=D*C % N
RETURN D这样,模幂运算就转化成了一系列的模乘运算。
算法可以写成如下的形式
如果我们现在用蒙哥马利样式稍作改变,就可以变成如下的形式:
以上就是蒙哥马利算法的全部,通过蒙哥马利算法中的约减运算,我们将大数运算中的模运算变成了移位操作,极大地提高了大数模乘的效率。
但是在以上的算法,可以发现还有两个变量的计算方式不是很清楚,一个是ω,前面说过ω=−N−1(modN) ,其实在算法中,我们看到,omega仅仅被用来做modb操作,所以事实上,我们只需要计算modb即可。
尽管N有可能是合数(因为两个素数的乘积不一定是素数),但通常N和ρ(也就是N和b)是互质的,也就是说Nϕ(b)=1(mob b)(费马定理),Nϕ(b)−1=N−1(mob b)
因为b=2ω,所以ϕ(b)=2(ω−1),写成算法是这样的
还有一个参数是ρ2,还记得前面说过ρ是怎么得出来吗,选定一个最小的k,使得bk》N,我们还知道N在b进制下是lN位,所以当k=lN的时候肯定是符合要求。
b=2ω 所以ρ=bk=(2ω)kρ2=(2w)k)2=22⋅k⋅ω=22⋅lN⋅ω,算法如下
至此整个蒙哥马利算法就全部说完了。通过这个算法,我们可以实现快速幂模。
C++实现
inline unsigned __int64 MulMod(unsigned __int64 a, unsigned __int64 b, unsigned __int64 n)
{
return a * b % n;
}
/*
模幂运算,返回值 x=base^pow mod n
*/
unsigned __int64 PowMod(unsigned __int64 base, unsigned __int64 pow, unsigned __int64 &n)
{
unsigned __int64 a=base, b=pow, c=1;
while(b)
{
while(!(b & 1))
{
b》》=1; //a=a * a % n; //
a=MulMod(a, a, n);
} b--; //c=a * c % n; //
c=MulMod(a, c, n);
} return c;
}
数论学家利用费马小定理研究出了多种素数测试方法,目前最快的算法是拉宾
米勒测试算法,其过程如下:
(1)计算奇数M,使得N=(2**r)*M+1
(2)选择随机数A《N
(3)对于任意i《r,若A**((2**i)*M) % N = N-1,则N通过随机数A的测试
(4)或者,若A**M % N = 1,则N通过随机数A的测试
(5)让A取不同的值对N进行5次测试,若全部通过则判定N为素数
若N 通过一次测试,则N 不是素数的概率为 25%,若N 通过t 次测试,则N 不是素数的概率为1/4**t。事实上取t 为5 时,N 不是素数的概率为 1/128,N 为素数的概率已经大于99.99%。
在实际应用中,可首先用300—500个小素数对N 进行测试,以提高拉宾米勒测试通过的概率,从而提高整体测试速度。而在生成随机素数时,选取的随机数最好让r=0,则可省去步骤(3) 的测试,进一步提高测试速度。
素数测试是RSA 选取秘钥的第一步,奇妙的是其核心运算与加解密时所需的运算完全一致:都是模幂运算。而模幂运算过程中中所需求解的欧几里德方程又恰恰正是选取密钥第二步所用的运算。可见整个RSA 算法具有一种整体的和谐。