shamir 门限 分散图文详解
概述
算法基本原理也就是多项式求值,详情见博客 [1]
从上面的算法思路中了解到,待加密明文 s ∈ Zp 。
事实上在实际该算法使用过程的,上面的数学表达需要装换为代码,待加密明文 s 可能存在多种情况,这造成有限群GF§取值多样,不便于算法代码实现。
- 我们能够将 待加密明文 s 拆解多个分块,每个 分块 都处于 属于某个 固定的有限域G 内。
- 以每个 分块 作为我们待加密的内容,这样我们就可以利用 固定的有限域G 实现算法。
- 加密时,利用 Shamir算法加密独立每个分块。
- 解密时分别解密每个分块,然后将各个分块 拼接到一起,就是 待加密明文 s
按照上述思路:
我们可以将 待加密明文 s 按照字节来拆分,每个字节(byte)能表示的范围是 [0, 255),这样就可以使用有限域 GF(256) 作为 Shamir算法的有限域。
实现解析
算法实现参考 [2]
设 Shamir算法的二元数为 (5, 3) 也就是 3 5 门限。
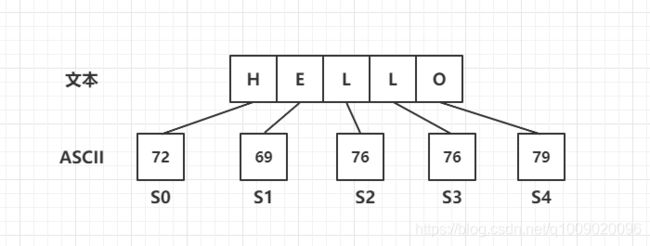
设 明文S为 HELLO,将S以字节拆分,可以拆分为5个部分: S 0 S_0 S0、 S 1 S_1 S1、 S 2 S_2 S2、 S 3 S_3 S3、 S 4 S_4 S4
加密需要生成多项式,对于上面的5个部分,也就需要生成 5个多项式,每个多项式的 a i , 0 = S n a_{i,0}=S_n ai,0=Sn, k = 3 k=3 k=3, i = 0... n − 1 i = 0...n-1 i=0...n−1
f 0 ( x ) = a 0 , 0 + a 0 , 1 x + a 0 , 2 x 2 m o d ( 255 ) , a 0 , 0 = 72 f_0(x) = a_{0,0} + a_{0,1}x + a_{0,2}x^2 mod(255), a_{0,0} = 72 f0(x)=a0,0+a0,1x+a0,2x2mod(255),a0,0=72
f 1 ( x ) = a 1 , 0 + a 1 , 1 x + a 1 , 2 x 2 m o d ( 255 ) , a 1 , 0 = 69 f_1(x) = a_{1,0} + a_{1,1}x + a_{1,2}x^2 mod(255), a_{1,0} = 69 f1(x)=a1,0+a1,1x+a1,2x2mod(255),a1,0=69
f 2 ( x ) = a 2 , 0 + a 2 , 1 x + a 2 , 2 x 2 m o d ( 255 ) , a 2 , 0 = 76 f_2(x) = a_{2,0} + a_{2,1}x + a_{2,2}x^2 mod(255), a_{2,0} = 76 f2(x)=a2,0+a2,1x+a2,2x2mod(255),a2,0=76
f 3 ( x ) = a 3 , 0 + a 3 , 1 x + a 3 , 2 x 2 m o d ( 255 ) , a 3 , 0 = 76 f_3(x) = a_{3,0} + a_{3,1}x + a_{3,2}x^2 mod(255), a_{3,0} = 76 f3(x)=a3,0+a3,1x+a3,2x2mod(255),a3,0=76
f 4 ( x ) = a 4 , 0 + a 4 , 1 x + a 4 , 2 x 2 m o d ( 255 ) , a 4 , 0 = 79 f_4(x) = a_{4,0} + a_{4,1}x + a_{4,2}x^2 mod(255), a_{4,0} = 79 f4(x)=a4,0+a4,1x+a4,2x2mod(255),a4,0=79
-
根据Shamir算法,需要为取 5个数( n = 5 n=5 n=5): x 1 x_1 x1、 x 2 x_2 x2、 x 3 x_3 x3、 x 4 x_4 x4、 x 5 x_5 x5,带入 f i ( x ) f_i(x) fi(x) 计算,得到
( x 1 , f i ( x 1 ) ) , ( x 2 , f i ( x 2 ) ) , ( x 3 , f i ( x 3 ) ) , ( x 4 , f i ( x 4 ) ) , ( x 5 , f i ( x 5 ) ) (x_1,f_i(x_1)), (x_2,f_i(x_2)), (x_3,f_i(x_3)), (x_4,f_i(x_4)), (x_5,f_i(x_5)) (x1,fi(x1)),(x2,fi(x2)),(x3,fi(x3)),(x4,fi(x4)),(x5,fi(x5)) -
由于S被拆为5份,5个多项式运算可以使用同一个 x 1 x_1 x1、 x 2 x_2 x2、 x 3 x_3 x3、 x 4 x_4 x4、 x 5 x_5 x5 序列,计算各自的加密分片。
5个分布的各自5个密钥对如下:
( x 1 , f 0 ( x 1 ) ) , ( x 2 , f 0 ( x 2 ) ) , ( x 3 , f 0 ( x 3 ) ) , ( x 4 , f 0 ( x 4 ) ) , ( x 5 , f 0 ( x 5 ) ) (x_1,f_0(x_1)), (x_2,f_0(x_2)), (x_3,f_0(x_3)), (x_4,f_0(x_4)), (x_5,f_0(x_5)) (x1,f0(x1)),(x2,f0(x2)),(x3,f0(x3)),(x4,f0(x4)),(x5,f0(x5))
( x 1 , f 1 ( x 1 ) ) , ( x 2 , f 1 ( x 2 ) ) , ( x 3 , f 1 ( x 3 ) ) , ( x 4 , f 1 ( x 4 ) ) , ( x 5 , f 1 ( x 5 ) ) (x_1,f_1(x_1)), (x_2,f_1(x_2)), (x_3,f_1(x_3)), (x_4,f_1(x_4)), (x_5,f_1(x_5)) (x1,f1(x1)),(x2,f1(x2)),(x3,f1(x3)),(x4,f1(x4)),(x5,f1(x5))
( x 1 , f 2 ( x 1 ) ) , ( x 2 , f 2 ( x 2 ) ) , ( x 3 , f 2 ( x 3 ) ) , ( x 4 , f 2 ( x 4 ) ) , ( x 5 , f 2 ( x 5 ) ) (x_1,f_2(x_1)), (x_2,f_2(x_2)), (x_3,f_2(x_3)), (x_4,f_2(x_4)), (x_5,f_2(x_5)) (x1,f2(x1)),(x2,f2(x2)),(x3,f2(x3)),(x4,f2(x4)),(x5,f2(x5))
( x 1 , f 3 ( x 1 ) ) , ( x 2 , f 3 ( x 2 ) ) , ( x 3 , f 3 ( x 3 ) ) , ( x 4 , f 3 ( x 4 ) ) , ( x 5 , f 3 ( x 5 ) ) (x_1,f_3(x_1)), (x_2,f_3(x_2)), (x_3,f_3(x_3)), (x_4,f_3(x_4)), (x_5,f_3(x_5)) (x1,f3(x1)),(x2,f3(x2)),(x3,f3(x3)),(x4,f3(x4)),(x5,f3(x5))
( x 1 , f 4 ( x 1 ) ) , ( x 2 , f 4 ( x 2 ) ) , ( x 3 , f 4 ( x 3 ) ) , ( x 4 , f 4 ( x 4 ) ) , ( x 5 , f 4 ( x 5 ) ) (x_1,f_4(x_1)), (x_2,f_4(x_2)), (x_3,f_4(x_3)), (x_4,f_4(x_4)), (x_5,f_4(x_5)) (x1,f4(x1)),(x2,f4(x2)),(x3,f4(x3)),(x4,f4(x4)),(x5,f4(x5))
令 y i = f i ( x ) y_i=f_i(x) yi=fi(x),将上述结果以表格形式呈现如下:
| y 1 y_1 y1 | y 2 y_2 y2 | y 3 y_3 y3 | y 4 y_4 y4 | y 5 y_5 y5 |
|---|---|---|---|---|
| f 0 ( x 1 ) f_0(x_1) f0(x1) | f 0 ( x 2 ) f_0(x_2) f0(x2) | f 0 ( x 3 ) f_0(x_3) f0(x3) | f 0 ( x 4 ) f_0(x_4) f0(x4) | f 0 ( x 5 ) f_0(x_5) f0(x5) |
| f 1 ( x 1 ) f_1(x_1) f1(x1) | f 1 ( x 2 ) f_1(x_2) f1(x2) | f 1 ( x 3 ) f_1(x_3) f1(x3) | f 1 ( x 4 ) f_1(x_4) f1(x4) | f 1 ( x 5 ) f_1(x_5) f1(x5) |
| f 2 ( x 1 ) f_2(x_1) f2(x1) | f 2 ( x 2 ) f_2(x_2) f2(x2) | f 2 ( x 3 ) f_2(x_3) f2(x3) | f 2 ( x 4 ) f_2(x_4) f2(x4) | f 2 ( x 5 ) f_2(x_5) f2(x5) |
| f 3 ( x 1 ) f_3(x_1) f3(x1) | f 3 ( x 2 ) f_3(x_2) f3(x2) | f 3 ( x 3 ) f_3(x_3) f3(x3) | f 3 ( x 4 ) f_3(x_4) f3(x4) | f 3 ( x 5 ) f_3(x_5) f3(x5) |
| f 4 ( x 1 ) f_4(x_1) f4(x1) | f 4 ( x 2 ) f_4(x_2) f4(x2) | f 4 ( x 3 ) f_4(x_3) f4(x3) | f 4 ( x 4 ) f_4(x_4) f4(x4) | f 4 ( x 5 ) f_4(x_5) f4(x5) |
x ∈ x 1 , x 2 , x 3 , x 4 , x 5 x \in x_1, x_2, x_3, x_4, x_5 x∈x1,x2,x3,x4,x5
- 我们的目的是将明文S加密,生成5个密钥。
- 而我们将S分解成了5个分片,每个分片加密后也是生成5个分片的加密密钥。
- 为了满足最终5个分片的需求,在最终每个密钥里面要含有,5个拆分的密钥的的密钥分片。
根据上述需求,将 x x x相同的 y i y_i yi,提到一行来(也就是旋转表格),如下:
| 名称 | y 1 y_1 y1 | y 2 y_2 y2 | y 3 y_3 y3 | y 4 y_4 y4 | y 5 y_5 y5 |
|---|---|---|---|---|---|
| 密钥分量1 | f 0 ( x 1 ) f_0(x_1) f0(x1) | f 1 ( x 1 ) f_1(x_1) f1(x1) | f 2 ( x 1 ) f_2(x_1) f2(x1) | f 3 ( x 1 ) f_3(x_1) f3(x1) | f 4 ( x 1 ) f_4(x_1) f4(x1) |
| 密钥分量2 | f 0 ( x 2 ) f_0(x_2) f0(x2) | f 1 ( x 2 ) f_1(x_2) f1(x2) | f 2 ( x 2 ) f_2(x_2) f2(x2) | f 3 ( x 2 ) f_3(x_2) f3(x2) | f 4 ( x 2 ) f_4(x_2) f4(x2) |
| 密钥分量3 | f 0 ( x 3 ) f_0(x_3) f0(x3) | f 1 ( x 3 ) f_1(x_3) f1(x3) | f 2 ( x 3 ) f_2(x_3) f2(x3) | f 3 ( x 3 ) f_3(x_3) f3(x3) | f 4 ( x 3 ) f_4(x_3) f4(x3) |
| 密钥分量4 | f 0 ( x 4 ) f_0(x_4) f0(x4) | f 1 ( x 4 ) f_1(x_4) f1(x4) | f 2 ( x 4 ) f_2(x_4) f2(x4) | f 3 ( x 4 ) f_3(x_4) f3(x4) | f 4 ( x 4 ) f_4(x_4) f4(x4) |
| 密钥分量5 | f 0 ( x 5 ) f_0(x_5) f0(x5) | f 1 ( x 5 ) f_1(x_5) f1(x5) | f 2 ( x 5 ) f_2(x_5) f2(x5) | f 3 ( x 5 ) f_3(x_5) f3(x5) | f 4 ( x 5 ) f_4(x_5) f4(x5) |
Shamir算法的密钥是一个二元组 ( x , y ) (x,y) (x,y),上面表格每行的 x x x都是相同的,因此还需要在表格里面放上 x x x。
| 名称 | y 1 y_1 y1 | y 2 y_2 y2 | y 3 y_3 y3 | y 4 y_4 y4 | y 5 y_5 y5 | x x x |
|---|---|---|---|---|---|---|
| 密钥分量1 | f 0 ( x 1 ) f_0(x_1) f0(x1) | f 1 ( x 1 ) f_1(x_1) f1(x1) | f 2 ( x 1 ) f_2(x_1) f2(x1) | f 3 ( x 1 ) f_3(x_1) f3(x1) | f 4 ( x 1 ) f_4(x_1) f4(x1) | x 1 x_1 x1 |
| 密钥分量2 | f 0 ( x 2 ) f_0(x_2) f0(x2) | f 1 ( x 2 ) f_1(x_2) f1(x2) | f 2 ( x 2 ) f_2(x_2) f2(x2) | f 3 ( x 2 ) f_3(x_2) f3(x2) | f 4 ( x 2 ) f_4(x_2) f4(x2) | x 2 x_2 x2 |
| 密钥分量3 | f 0 ( x 3 ) f_0(x_3) f0(x3) | f 1 ( x 3 ) f_1(x_3) f1(x3) | f 2 ( x 3 ) f_2(x_3) f2(x3) | f 3 ( x 3 ) f_3(x_3) f3(x3) | f 4 ( x 3 ) f_4(x_3) f4(x3) | x 3 x_3 x3 |
| 密钥分量4 | f 0 ( x 4 ) f_0(x_4) f0(x4) | f 1 ( x 4 ) f_1(x_4) f1(x4) | f 2 ( x 4 ) f_2(x_4) f2(x4) | f 3 ( x 4 ) f_3(x_4) f3(x4) | f 4 ( x 4 ) f_4(x_4) f4(x4) | x 4 x_4 x4 |
| 密钥分量5 | f 0 ( x 5 ) f_0(x_5) f0(x5) | f 1 ( x 5 ) f_1(x_5) f1(x5) | f 2 ( x 5 ) f_2(x_5) f2(x5) | f 3 ( x 5 ) f_3(x_5) f3(x5) | f 4 ( x 5 ) f_4(x_5) f4(x5) | x 5 x_5 x5 |
- 表格中的每一行就是一个密钥分量。
- 每个密钥分量也就是一个
byte数组。 - Shamir算法的运算结果也就是一个
byte[][]
实例
还是以上面的HELLO为例,拆分字符
f 0 ( x ) = 72 + 114 x + 242 x 2 m o d ( 255 ) f_0(x) = 72 + 114x + 242x^2 mod(255) f0(x)=72+114x+242x2mod(255)
f 1 ( x ) = 69 + 32 x + 90 x 2 m o d ( 255 ) f_1(x) = 69 + 32x + 90x^2 mod(255) f1(x)=69+32x+90x2mod(255)
f 2 ( x ) = 76 + 174 x + 98 x 2 m o d ( 255 ) f_2(x) = 76 + 174x + 98x^2 mod(255) f2(x)=76+174x+98x2mod(255)
f 3 ( x ) = 76 + 73 x + 29 x 2 m o d ( 255 ) f_3(x) = 76 + 73x + 29x^2 mod(255) f3(x)=76+73x+29x2mod(255)
f 4 ( x ) = 79 + 221 x + 29 x 2 m o d ( 255 ) f_4(x) = 79 + 221x + 29x^2 mod(255) f4(x)=79+221x+29x2mod(255)
| a 0 a_0 a0 | a 1 a_1 a1 | a 2 a_2 a2 |
|---|---|---|
| 72 | 114 | 242 |
| 69 | 32 | 90 |
| 76 | 174 | 98 |
| 76 | 73 | 29 |
| 79 | 221 | 29 |
取5个随机数 x x x
x 1 = 64 , x 2 = 5 , x 3 = 121 , x 4 = 117 , x 5 = 129 x_1=64, x_2=5, x_3=121, x_4=117, x_5=129 x1=64,x2=5,x3=121,x4=117,x5=129
5个分量为
| 名称 | y 1 y_1 y1 | y 2 y_2 y2 | y 3 y_3 y3 | y 4 y_4 y4 | y 5 y_5 y5 | x x x |
|---|---|---|---|---|---|---|
| 密钥分量1 | 221 | 194 | 230 | 209 | 232 | 64 |
| 密钥分量2 | 162 | 104 | 116 | 236 | 29 | 5 |
| 密钥分量3 | 123 | 6 | 132 | 241 | 14 | 121 |
| 密钥分量4 | 126 | 59 | 132 | 122 | 47 | 117 |
| 密钥分量5 | 197 | 243 | 142 | 162 | 65 | 129 |
参考文献
[1]. Shamir密钥分享算法简析 . Mythsman . 2015.10.07 . https://blog.mythsman.com/post/5d2fe659976abc05b345449c/
[2]. github . hashicorp . vault . https://github.com/kinvolk/go-shamir/blob/master/vendor/github.com/hashicorp/vault/shamir/shamir.go