365天深度学习训练营-第J3周：DenseNet算法实战与解析

目录

  一、前言

二、论文解读

1、DenseNet的优势

2、设计理念

 3、网络结构

 4、与其他算法进行对比

三、代码复现

1、使用Pytorch实现DenseNet

2、使用Tensorflow实现DenseNet网络

四、分析总结

---

  一、前言

• 本文为365天深度学习训练营 中的学习记录博客
• 原作者：K同学啊|接辅导、项目定制

● 难度：夯实基础⭐⭐
● 语言：Python3、Pytorch3
● 时间：2月18日-2月14日
要求：

1.根据本文的Pytorch代码，编写Tensorflow代码
2.了解DenseNet和ResnetV的区别
3.改进地方可以迁移到哪里呢

二、论文解读

论文：Densely Connected Convolutional Networks

       众所周知，最近一两年卷积神经网络提高效果的方向，要么深（比如ResNet，解决了网络深时候的梯度消失问题）要么宽（比如GoogleNet的Inception），而作者则是从特征图入手，通过对特征图的极致利用达到更好的效果和更少的参数。

1、DenseNet的优势

• 减轻了vanishing-gradient（梯度消失）

这种连接方式使得特征和梯度的传递更加有效，网络也就更加容易训练。每一层都可以直接利用损失函数的梯度以及最开始的输入信息，相当于是一种隐形的深度监督（implicit deep supervision），这有助于训练更深的网络。前面提到过梯度消失问题在网络深度越深的时候越容易出现，原因就是输入信息和梯度信息在很多层之间传递导致的，而现在这种密集连接相当于每一层都直接连接输入和损失，因此就可以减轻梯度消失现象，这样构建更深的网络不是问题。

• 加强了特征的传递，更有效地利用了特征

每层的输出特征图都是之后所有层的输入。

• 一定程度上较少了参数数量

DenseNets的稠密连接模块（dense block）的一个优点是它比传统的卷积网络有更少的参数，因为它不需要再重新学习多余的特征图。传统的前馈结构可以被看成一种层与层之间状态传递的算法。每一层接收前一层的状态，然后将新的状态传递给下一层。它改变了状态，但也传递了需要保留的信息。ResNets将这种信息保留的更明显，因为它加入了自身变换（identity transformations）。最近很多关于ResNets的研究都表明ResNets的很多层是几乎没有起作用的，可以在训练时随机的丢掉。DenseNet结构中，增加到网络中的信息与保留的信息有着明显的不同。DenseNet的dense block中每个卷积层都很窄（例如每一层有12个滤波器），仅仅增加小数量的特征图到网络的“集体知识”（collective knowledge），并且保持这些特征图不变——最后的分类器基于网络中的所有特征图进行预测。

另外作者还观察到这种密集连接有正则化的效果，因此对于过拟合有一定的抑制作用，因为参数减少了，所以过拟合现象减轻。
参考文章

2、设计理念

DenseNet 的想法很大程度上源于一个叫做随机深度网络（Deep networks with stochastic depth）工作。当时我们提出了一种类似于 Dropout 的方法来改进ResNet。我们发现在训练过程中的每一步都随机地「扔掉」（drop）一些层，可以显著的提高 ResNet 的泛化性能。这个方法的成功至少带给我们两点启发：

• 首先，它说明了神经网络其实并不一定要是一个递进层级结构，也就是说网络中的某一层可以不仅仅依赖于紧邻的上一层的特征，而可以依赖于更前面层学习的特征。想像一下在随机深度网络中，当第 l 层被扔掉之后，第 l+1 层就被直接连到了第 l-1 层；当第 2 到了第 l 层都被扔掉之后，第 l+1 层就直接用到了第 1 层的特征。因此，随机深度网络其实可以看成一个具有随机密集连接的 DenseNet。

• 其次，我们在训练的过程中随机扔掉很多层也不会破坏算法的收敛，说明了 ResNet 具有比较明显的冗余性，网络中的每一层都只提取了很少的特征（即所谓的残差）。实际上，我们将训练好的 ResNet 随机的去掉几层，对网络的预测结果也不会产生太大的影响。既然每一层学习的特征这么少，能不能降低它的计算量来减小冗余呢？

DenseNet 的设计正是基于以上两点观察。我们让网络中的每一层都直接与其前面层相连，实现特征的重复利用；同时把网络的每一层设计得特别「窄」，即只学习非常少的特征图（最极端情况就是每一层只学习一个特征图），达到降低冗余性的目的。这两点也是 DenseNet 与其他网络最主要的不同。需要强调的是，第一点是第二点的前提，没有密集连接，我们是不可能把网络设计得太窄的，否则训练会出现欠拟合（under-fitting）现象，即使 ResNet 也是如此。

 3、网络结构

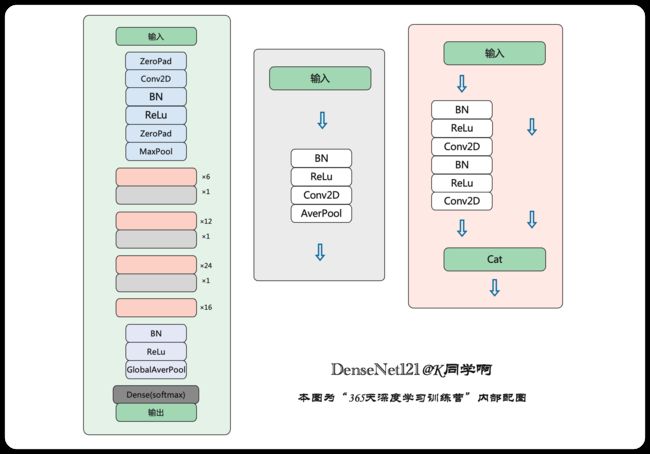
     CNN网络一般要经过Pooling或者stride>1的Conv来降低特征图的大小，而DenseNet的密集连接方式需要特征图大小保持一致。为了解决这个问题，DenseNet网络中使用DenseBlock+Transition的结构，其中DenseBlock是包含很多层的模块，每个层的特征图大小相同，层与层之间采用密集连接方式。而Transition层是连接两个相邻的DenseBlock，并且通过Pooling使特征图大小降低。图5给出了DenseNet的网路结构，它共包含4个DenseBlock，各个DenseBlock之间通过Transition层连接在一起。

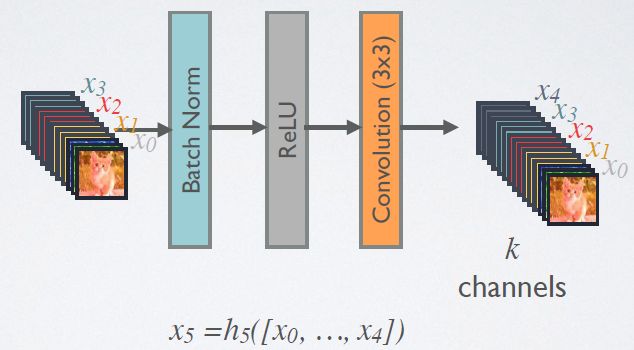
       在DenseBlock中，各个层的特征图大小一致，可以在channel维度上连接。DenseBlock中的非线性组合函数H(·)的是 BN+ReLU+3x3 Conv 的结构，如图6所示。另外值得注意的一点是，与ResNet不同，所有DenseBlock中各个层卷积之后均输出k个特征图，即得到的特征图的channel数为k，或者说采用k个卷积核。k在DenseNet称为growth rate，这是一个超参数。一般情况下使用较小的k（比如12），就可以得到较佳的性能。假定输入层的特征图的channel数为k0，那么l层输入的channel数为，因此随着层数增加，尽管k设定得较小，DenseBlock的输入会非常多，不过这是由于特征重用所造成的，每个层仅有k个特征是自己独有的。

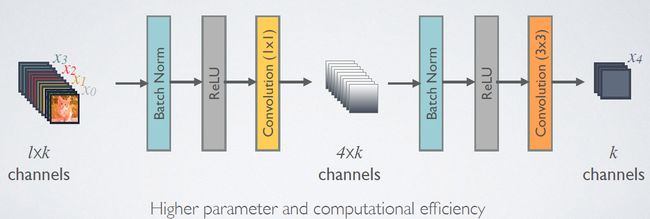
       由于后面层的输入会非常大，DenseBlock内部可以采用bottleneck层来减少计算量，主要是原有的结构中增加1x1 Conv，如图7所示，即BN+ReLU+1x1 Conv+BN+ReLU+3x3 Conv，称为DenseNet-B结构。其中1x1 Conv得到4k个特征图它起到的作用是降低特征数量，从而提升计算效率。

       对于Transition层，，它主要是连接两个相邻的DenseBlock，并且降低特征图大小。Transition层包括一个1x1的卷积和2x2的AvgPooling，结构为BN+ReLU+1x1Conv+2x2AvgPooling。另外，Transition层可以起到压缩模型的作用。假定层的上接DenseBlock得到的特征图channels数为m，Transition层可以产生【θm】个特征（通过卷积层），其中 是压缩系数θ∈（0，1]（compression rate）。当 θ=1时，特征个数经过Transition层没有变化，即无压缩，而当压缩系数小于1时，这种结构称为DenseNet-C，文中使用θ=0.5。对于使用bottleneck层的DenseBlock结构和压缩系数小于1的Transition组合结构称为DenseNet-BC。

       对于ImageNet数据集，图片输入大小为224×224，网络结构采用包含4个DenseBlock的DenseNet-BC，其首先是一个stride=2的7x7卷积层，然后是一个stride=2的3x3 MaxPooling层，后面才进入DenseBlock。ImageNet数据集所采用的网络配置如表1所示：

 4、与其他算法进行对比

三、代码复现

1、使用Pytorch实现DenseNet

•       这里我们采用了Pytorch的框架来实现DenseNet，首先实现DenseBlock中的内部结构，这里是BN+ReLU+1×1Conv+BN+ReLU+3×3Conv结构，最后也加入dropout层用于训练过程。

class _DenseLayer(nn.Module):
    def __init__(self, num_input_features, growth_rate, bn_size, drop_rate, efficient=False):
        super(_DenseLayer, self).__init__()
        self.add_module('norm1', nn.BatchNorm2d(num_input_features)),
        self.add_module('relu1', nn.ReLU(inplace=True)),
        self.add_module('conv1', nn.Conv2d(num_input_features, bn_size * growth_rate,
                        kernel_size=1, stride=1, bias=False)),
        self.add_module('norm2', nn.BatchNorm2d(bn_size * growth_rate)),
        self.add_module('relu2', nn.ReLU(inplace=True)),
        self.add_module('conv2', nn.Conv2d(bn_size * growth_rate, growth_rate,
                        kernel_size=3, stride=1, padding=1, bias=False)),
        self.drop_rate = drop_rate
        self.efficient = efficient

    def forward(self, *prev_features):
        bn_function = _bn_function_factory(self.norm1, self.relu1, self.conv1)
        if self.efficient and any(prev_feature.requires_grad for prev_feature in prev_features):
            bottleneck_output = cp.checkpoint(bn_function, *prev_features)
        else:
            bottleneck_output = bn_function(*prev_features)
        new_features = self.conv2(self.relu2(self.norm2(bottleneck_output)))
        if self.drop_rate > 0:
            new_features = F.dropout(new_features, p=self.drop_rate, training=self.training)
        return new_features

• 实现DenseBlock模块，内部是密集连接方式（输入特征数线性增长）： 

class _DenseBlock(nn.Module):
    def __init__(self, num_layers, num_input_features, bn_size, growth_rate, drop_rate, efficient=False):
        super(_DenseBlock, self).__init__()
        for i in range(num_layers):
            layer = _DenseLayer(
                num_input_features + i * growth_rate,
                growth_rate=growth_rate,
                bn_size=bn_size,
                drop_rate=drop_rate,
                efficient=efficient,
            )
            self.add_module('denselayer%d' % (i + 1), layer)

    def forward(self, init_features):
        features = [init_features]
        for name, layer in self.named_children():
            new_features = layer(*features)
            features.append(new_features)
        return torch.cat(features, 1)

• 实现Transition层，它主要是一个卷积层和一个池化层：

class _Transition(nn.Sequential):
    def __init__(self, num_input_features, num_output_features):
        super(_Transition, self).__init__()
        self.add_module('norm', nn.BatchNorm2d(num_input_features))
        self.add_module('relu', nn.ReLU(inplace=True))
        self.add_module('conv', nn.Conv2d(num_input_features, num_output_features,
                                          kernel_size=1, stride=1, bias=False))
        self.add_module('pool', nn.AvgPool2d(kernel_size=2, stride=2))

• 最后我们实现DenseNet网络： 

class DenseNet(nn.Module):
    r"""Densenet-BC model class, based on
    `"Densely Connected Convolutional Networks" `
    Args:
        growth_rate (int) - how many filters to add each layer (`k` in paper)
        block_config (list of 3 or 4 ints) - how many layers in each pooling block
        num_init_features (int) - the number of filters to learn in the first convolution layer
        bn_size (int) - multiplicative factor for number of bottle neck layers
            (i.e. bn_size * k features in the bottleneck layer)
        drop_rate (float) - dropout rate after each dense layer
        num_classes (int) - number of classification classes
        small_inputs (bool) - set to True if images are 32x32. Otherwise assumes images are larger.
        efficient (bool) - set to True to use checkpointing. Much more memory efficient, but slower.
    """
    def __init__(self, growth_rate=12, block_config=(16, 16, 16), compression=0.5,
                 num_init_features=24, bn_size=4, drop_rate=0,
                 num_classes=10, small_inputs=True, efficient=False):

        super(DenseNet, self).__init__()
        assert 0 < compression <= 1, 'compression of densenet should be between 0 and 1'

        # First convolution
        if small_inputs:
            self.features = nn.Sequential(OrderedDict([
                ('conv0', nn.Conv2d(3, num_init_features, kernel_size=3, stride=1, padding=1, bias=False)),
            ]))
        else:
            self.features = nn.Sequential(OrderedDict([
                ('conv0', nn.Conv2d(3, num_init_features, kernel_size=7, stride=2, padding=3, bias=False)),
            ]))
            self.features.add_module('norm0', nn.BatchNorm2d(num_init_features))
            self.features.add_module('relu0', nn.ReLU(inplace=True))
            self.features.add_module('pool0', nn.MaxPool2d(kernel_size=3, stride=2, padding=1,
                                                           ceil_mode=False))

        # Each denseblock
        num_features = num_init_features
        for i, num_layers in enumerate(block_config):
            block = _DenseBlock(
                num_layers=num_layers,
                num_input_features=num_features,
                bn_size=bn_size,
                growth_rate=growth_rate,
                drop_rate=drop_rate,
                efficient=efficient,
            )
            self.features.add_module('denseblock%d' % (i + 1), block)
            num_features = num_features + num_layers * growth_rate
            if i != len(block_config) - 1:
                trans = _Transition(num_input_features=num_features,
                                    num_output_features=int(num_features * compression))
                self.features.add_module('transition%d' % (i + 1), trans)
                num_features = int(num_features * compression)

        # Final batch norm
        self.features.add_module('norm_final', nn.BatchNorm2d(num_features))

        # Linear layer
        self.classifier = nn.Linear(num_features, num_classes)

        # Initialization
        for name, param in self.named_parameters():
            if 'conv' in name and 'weight' in name:
                n = param.size(0) * param.size(2) * param.size(3)
                param.data.normal_().mul_(math.sqrt(2. / n))
            elif 'norm' in name and 'weight' in name:
                param.data.fill_(1)
            elif 'norm' in name and 'bias' in name:
                param.data.fill_(0)
            elif 'classifier' in name and 'bias' in name:
                param.data.fill_(0)

    def forward(self, x):
        features = self.features(x)
        out = F.relu(features, inplace=True)
        out = F.adaptive_avg_pool2d(out, (1, 1))
        out = torch.flatten(out, 1)
        out = self.classifier(out)
        return 

2、使用Tensorflow实现DenseNet网络

• DenseLayer

class  DenseLayer(Model):
    def __init__(self,bottleneck_size,growth_rate):
        super().__init__()
        self.filters=growth_rate
        self.bottleneck_size=bottleneck_size
        self.b1=BatchNormalization()
        self.a1=Activation('relu')
        self.c1=Conv2D(filters=self.bottleneck_size,kernel_size=(1,1),strides=1)
        self.b2=BatchNormalization()
        self.a2=Activation('relu')
        self.c2=Conv2D(filters=32,kernel_size=(3,3),strides=1,padding='same')
    def call(self,*x):
        x=tf.concat(x,2)
        x=self.b1(x)
        x=self.a1(x)
        x=self.c1(x)
        x=self.b2(x)
        x=self.a2(x)
        y=self.c2(x)    
        return y

• Block

class DenseBlock(Model):
    def __init__(self,Dense_layers_num,growth_rate):#Dense_layers_num每个denseblock中的denselayer数，growth
        super().__init__()
        self.Dense_layers_num=Dense_layers_num
        self.Dense_layers=[]
        bottleneck_size=4*growth_rate
        for i in range(Dense_layers_num):
            layer=DenseLayer(bottleneck_size,growth_rate)
            self.Dense_layers.append(layer)
    def call(self,input):
        x=[input]
        for layer in self.Dense_layers:
            output=layer(*x)
            x.append(output)
        y=tf.concat(x,2)
        return y

• Transition

class Transition(Model):
    def __init__(self,filters):
        super().__init__()
        self.b=BatchNormalization()
        self.a=Activation('relu')
        self.c=Conv2D(filters=filters,kernel_size=(1,1),strides=1)
        self.p=AveragePooling2D(pool_size=(2,2),strides=2)
        
    def call(self,x):
        x=self.b(x)
        x=self.a(x)
        x=self.c(x)
        y=self.p(x)
        return y 

• DenseNet

class DenseNet(Model):
    def __init__(self,block_list=[6,12,24,16],compression_rate=0.5,filters=64):
        super().__init__()
        growth_rate=32
        self.padding=ZeroPadding2D(((1,2),(1,2)))
        self.c1=Conv2D(filters=filters,kernel_size=(7,7),strides=2,padding='valid')
        self.b1=BatchNormalization()
        self.a1=Activation('relu')
        self.p1=MaxPooling2D(pool_size=(3,3),strides=2,padding='same')
        self.blocks=tf.keras.models.Sequential()
        input_channel=filters
        for i,layers_in_block in enumerate(block_list):
            if i<3 :
                self.blocks.add(DenseBlock(layers_in_block,growth_rate))
                block_out_channels=input_channel+layers_in_block*growth_rate
                self.blocks.add(Transition(filters=block_out_channels*0.5))
            if i==3:
                self.blocks.add(DenseBlock(Dense_layers_num=layers_in_block,growth_rate=growth_rate))
        self.p2=GlobalAveragePooling2D()
        self.d2=Dense(1000,activation='softmax') 
    def call(self,x):
        x=self.padding(x)
        x=self.c1(x)
        x=self.b1(x)
        x=self.a1(x)
        x=self.p1(x)
        x=self.blocks(x)
        x=self.p2(x)
        y=self.d2(x)
        return y
model=DenseNet()

四、分析总结

分析：

该文章提出的DenseNet核心思想在于建立了不同层之间的连接关系，充分利用了feature，进一步减轻了梯度消失问题，加深网络不是问题，而且训练效果非常好。另外，利用bottleneck layer，Translation layer以及较小的growth rate使得网络变窄，参数减少，有效抑制了过拟合，同时计算量也减少了。DenseNet优点很多，而且在和ResNet的对比中优势还是非常明显的。

DenseNet具有如下优点：

• 1.信息流通更为顺畅；
• 2.支持特征重用；
• 3.网络更窄

由于DenseNet需要在内存中保存Dense Block的每个节点的输出，此时需要极大的显存才能支持较大规模的DenseNet，这也导致了现在工业界主流的算法依旧是残差网络。

讨论

　　从表面来看，DenseNets和ResNets很像：方程（2）和方程（1）的不同主要在输入 Hl(*) （进行拼接而不是求和）。然而，这个小的改变却是给这两种网络结构的性能带来了很大的差异。

模型简化性（Model Compactness）。将输入进行连接的直接结果是，DenseNets 每一层学到的特征图都可以被以后的任一层利用。该方式有助于网络特征的重复利用，也因此得到了更简化的模型。

DenseNet-BC 是参数效率最高的一个 DenseNet 版本。此外，DenseNet-BC 仅仅用了大概 ResNets 1/3 的参数量就获得了相近的准确率（中图）。该结果与图3的结果相一致。如图4右图，仅有 0.8M 参数量的 DenseNet-BC 和有 10.2M参数的 101-ResNets 准确率相近。

隐含的深度监督（implicit deep supervision）。稠密卷积网络可以提升准确率的一个解释是，由于更短的连接，每一层都可以从损失函数中获得监督信息。可以将 DenseNets 理解为一种“深度监督”（Deep supervision）。深度监督的好处已经在之前的深度监督网络（DSN）中说明，该网络在每一隐含层都加了分类器，迫使中间层也学习判断特征（discriminative features）。

　　DenseNet和深度监督网络相似：网络最后的分类器通过最多两个或三个过度层为所有层提供监督信息。然而，DenseNets的损失含数字和梯度不是很复杂，这是因为所有层之间共享了损失函数。

随机 VS 确定连接。稠密卷积网络与残差网络的随机深度正则化（stochastic depth regularzaion）之间有着有趣的关系。在随机深度中，残差网络随机丢掉一些层，直接将周围的层进行连接。因为池化层没有丢掉，所以该网络和DenseNet有着相似的连接模式：以一定的小概率对相同池化层之间的任意两层进行直接连接——如果中间层随机丢掉的话。尽管这两个方法在根本上是完全不一样的，但是 DenseNet 关于随机深度的解释会给该正则化的成功提供依据。

　　总结一下：DenseNet和stochastic depth的关系，在 stochastic depth中，residual中的layers在训练过程中会被随机drop掉，其实这就会使得相邻层之间直接连接，这和DenseNet是很像的。

特征重复利用。根据设计来看，DenseNets 允许每一层获得之前所有层（尽管一些是通过过渡层）的特征图。我们做了一个实验来判断是否训练的网络可以重复利用这个机会。我们首先在 C10+ 数据上训练了 L=40, k=12 的 DenseNet。对于每个 block的每个卷积层 l，我们计算其与 s 层连接的平均权重。三个 dense block 的热度图如图 5 所示。平均权重表示卷积层与它之前层的依赖关系。位置（l, s）处的一个红点表示层 l 充分利用了前 s 层产生的特征图。由图中可以得到以下结论：

• 1，在同一个 block 中，所有层都将他的权重传递给其他层作为输入。这表明早期层提取的特征可以被同一个 dense block 下深层所利用
• 2，过渡层的权重也可以传递给之前 dense block 的所有层，也就是说 DenseNet 的信息可以以很少的间接方式从第一层流向最后一层
• 3，第二个和第三个 dense block 内的所有层分配最少的权重给过渡层的输出，表明过渡层输出很多冗余特征。这和 DenseNet-BC 强大的结果有关系
• 4，尽管最后的分类器也使用通过整个 dense block 的权重，但似乎更关注最后的特征图，表明网络的最后也会产生一些高层次的特征。