基于FPGA实现正弦插值算法
1、正弦插值的算法分析
1.1 信号在时域与频域的映射关系
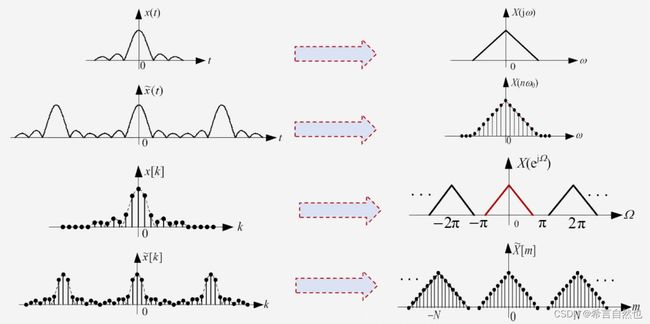
在进行正弦算法分析之前,我们回顾一下《数字信号处理》课程中,对于信号在时域与频域之间的映射关系,如下图。
对于上图中的原始信号x(t),使用ADC对信号进行采样,即实现了时域信号的离散化,得到x[k]。根据时域与频域之间的映射关系:时域的离散化对应着频域的周期化,即x[k]的频域响应为![]() 。
。
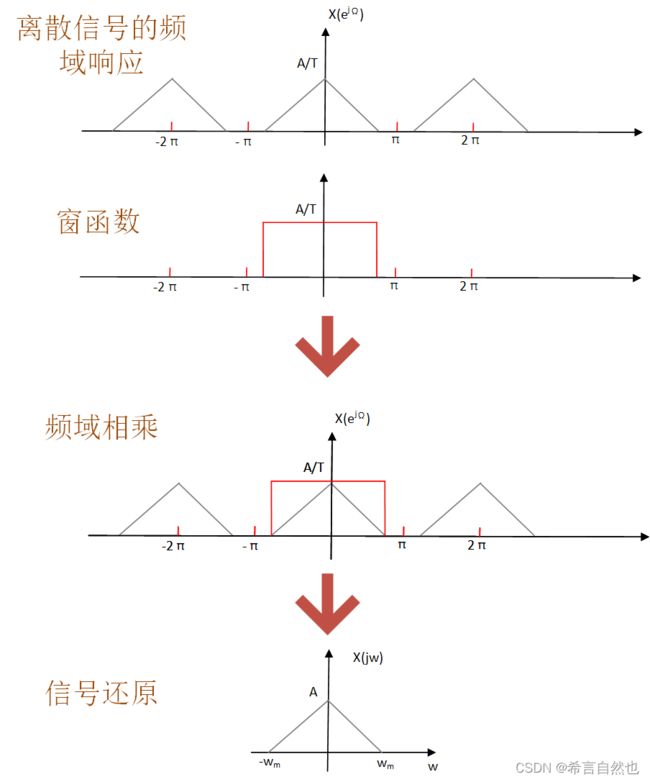
那么离散化的x[k]如何还原为原来的x(t)呢?时域上分析较为复杂,我们可以从频域上进行分析,即如何将频域响应![]() 还原成X(jw)。这样就比较直观了,只需要截取
还原成X(jw)。这样就比较直观了,只需要截取![]() 一个周期的信号,就可以还原成X(jw),示例如下图。
一个周期的信号,就可以还原成X(jw),示例如下图。
1.2 sinc函数
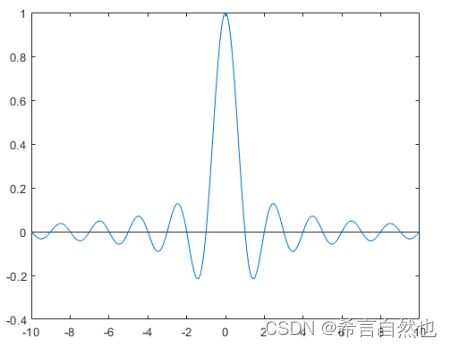
上面用到的窗函数,实际上是一个理想的低通滤波器,其时域形态是什么样子的呢?如下图。
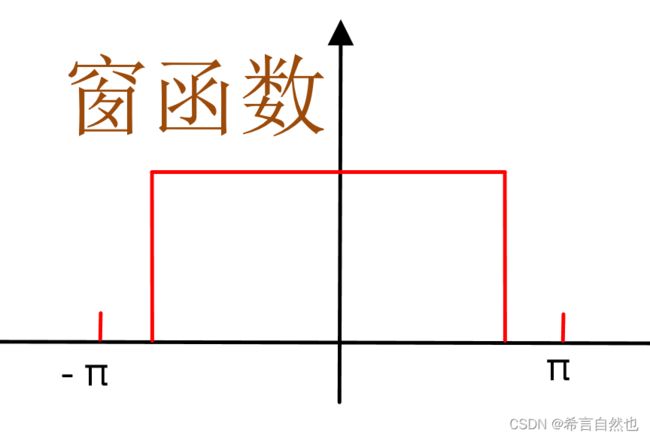
其时域形态公式:![]() ,sinc函数在频域上是一个矩形的方窗,如下图。
,sinc函数在频域上是一个矩形的方窗,如下图。
1.3 使用sinc函数实现正弦插值的算法分析
综上所述,对于我们可以使用sinc函数实现离散信号还原为连续信号,即使用sinc函数实现离散信号的无限插值。
而频域的乘积对应着时域的卷积,因此我们可以将离散的采样信号与sinc函数进行卷积运算,从而获得插值后的信号。
![]()
其中,y(n)为插值后信号;x(n)为待插值的离散信号;h(n)为sinc函数,也称为插值核或者插值因子。
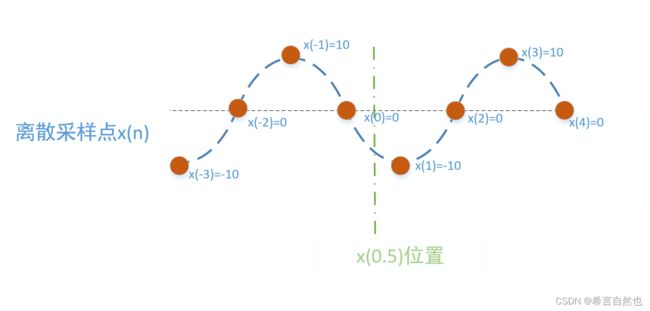
假设有一个离散信号x(n),含有8个离散点,x(n)={-10,0,10,0,-10,0,10,0};如下图:
我们使用前后共计8个原始采样点,来求插值点x(0.5)的数值。套用上面描述的公式![]() ,即x(0.5)=x(-3)h(0.5-(-3)) + x(-2)h(0.5-(-2)) + x(-1)h(0.5-(-1)) + x(0)h(0.5-(0)) + x(1)h(0.5-(1)) + x(2)h(0.5-(2)) + x(3)h(0.5-(3)) =-6.3056,即求得插值点的数值。
,即x(0.5)=x(-3)h(0.5-(-3)) + x(-2)h(0.5-(-2)) + x(-1)h(0.5-(-1)) + x(0)h(0.5-(0)) + x(1)h(0.5-(1)) + x(2)h(0.5-(2)) + x(3)h(0.5-(3)) =-6.3056,即求得插值点的数值。
根据这种思想,我们可以无限的求得每个插值点的数值。那么如何在工程也能够中使用sinc函数实现信号的插值,是我们接下来要讲述的。
2、使用matlab计算插值核
在使用FPGA实现插值算法时,由于sinc函数的计算实现起来比较消耗硬件资源,所以一般预先计算好插值核存放在ROM或者寄存器中,直接进行调用。
假设我们要使用前后8个点计算插值,插值倍数为10,那么使用matlab计算插值核的代码如下:
interp_mul = 10; %插值倍数为10
orig_point_num = 8;%原始点数8个
coe_group = zeros(interp_mul,orig_point_num); %定义系数组
for group = 1:1:interp_mul %计算interp_mul组系数
for Hn = 1:1:orig_point_num %计算每组系数的orig_point_num个加权值
if(group == 1)
if(Hn==4)
coe_group(group,Hn) = 1; %原始点保持数据不变[0,0,0,1,0,0,0,0]
else
coe_group(group,Hn) = 0; %原始点保持数据不变[0,0,0,1,0,0,0,0]
end
else
coe_group(group,Hn) = sinc(4- Hn + 0.1*(group-1));%找规律映射
end
end
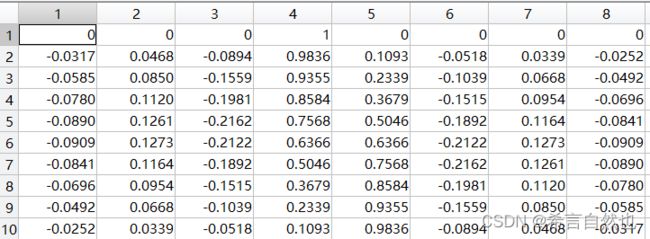
end运行结果保存在coe_group数组中,结果如下:
上述算法计算得到的插值核为小数,而FPGA计算小数运算时,需要现将数值左移相应位数进行放大,方便进行计算,输出结果时,截取高bit即可。由于后续FPGA实现卷积和时使用18bits的插值核进行运算,因此实际工程中的matlab代码如下:
interp_mul = 10; %插值倍数为10
orig_point_num = 8;%原始点数8个
coe_group = zeros(interp_mul,orig_point_num); %定义系数组
for group = 1:1:interp_mul %计算interp_mul组系数
for Hn = 1:1:orig_point_num %计算每组系数的orig_point_num个加权值
if(group == 1)
if(Hn==4)
coe_group(group,Hn) = 2^17 -1; %原始点保持数据不变[0,0,0,1,0,0,0,0]
else
coe_group(group,Hn) = 0; %原始点保持数据不变[0,0,0,1,0,0,0,0]
end
else
coe_group(group,Hn) = sinc(4- Hn + 0.1*(group-1)) *2^17;%找规律映射,小数放大2^17倍
end
end
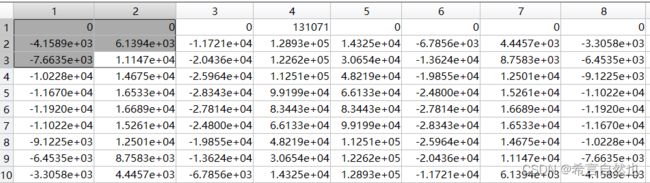
end结果如下:
3、使用FPGA实现离散采样点的插值
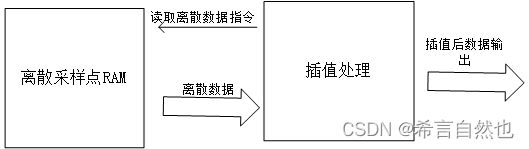
本文中仅使用一个测试程序,说明FPGA实现插值的原理,结构相对简单,架构图如下:
离散采样RAM模块代码如下:
module disc_samp_gen(
input clk,
input disc_rd,//读待插值数据标志
output [7:0] disc_samp //离散采样点输出 有符号数据
);
reg [1:0]addra=0;
always@(posedge clk)
begin
if(disc_rd)
addra <= addra + 1'b1;
end
DataSrc_ROM DataSrc_ROM (
.clka(clk), // input wire clka
.addra(addra), // input wire [1 : 0] addra
.douta(disc_samp) // output wire [7 : 0] douta
);
endmodule插值处理模块,主要通过乘法器实现卷积和,如下:
module sinc_process(
input clk,
input sinc_en,//插值使能标志
input [7:0]disc_samp,//待插值数据,有符号数
output disc_rd,//读取插值数据标志
output sinc_valid,//插值数据有效标志
output [7:0]sinc_data//插值后数据
);
//插值倍数10,使用8个离散采样点进行插值处理
第0组插值核
//localparam [17:0] group0_coe[7:0] = {18'h0,18'h0,18'h0,18'h0,
// 18'h1FFFF,18'h0,18'h0,18'h0};//临时粗略将18'h1FFFF视为1
第1组插值核
//localparam [17:0] group1_coe[7:0] = {18'h3F317,18'h0115D,18'h3E57F,18'h037F5,
// 18'h1F79E,18'h3D238,18'h017FB,18'h3EFC2};
第2组插值核
//localparam [17:0] group2_coe[7:0] = {18'h3E6CB,18'h02236,18'h3CAC8,18'h077BE,
// 18'h1DEF8,18'h3B02C,18'h02B8A,18'h3E211};
第3组插值核
//localparam [17:0] group3_coe[7:0] = {18'h3DC5E,18'h030D5,18'h3B272,18'h0BC5B,
// 18'h1B77F,18'h39A94,18'h03953,18'h3D80C};
第4组插值核
//localparam [17:0] group4_coe[7:0] = {18'h3D4F2,18'h03B9D,18'h39F21,18'h10254,
// 18'h1837E,18'h3914A,18'h04095,18'h3D26A};
第5组插值核
//localparam [17:0] group5_coe[7:0] = {18'h3D170,18'h04130,18'h3935A,18'h145F3,
// 18'h145F3,18'h3935A,18'h04130,18'h3D170};
第6组插值核
//localparam [17:0] group6_coe[7:0] = {18'h3D26A,18'h04095,18'h3914A,18'h1837E,
// 18'h10254,18'h39F21,18'h03B9D,18'h3D4F2};
第7组插值核
//localparam [17:0] group7_coe[7:0] = {18'h3D80C,18'h03953,18'h39A94,18'h1B77F,
// 18'h0BC5B,18'h3B272,18'h030D5,18'h3DC5E};
第8组插值核
//localparam [17:0] group8_coe[7:0] = {18'h3E211,18'h02B8A,18'h3B02C,18'h1DEF8,
// 18'h077BE,18'h3CAC8,18'h02236,18'h3E6CB};
第9组插值核
//localparam [17:0] group9_coe[7:0] = {18'h3EFC2,18'h017FB,18'h3D238,18'h1F79E,
// 18'h037F5,18'h3E57F,18'h0115D,18'h3F317};
//第0组插值核
localparam [17:0] group0_coe[7:0] = {18'h0,18'h0,18'h0,18'h1FFFF,18'h0,18'h0,18'h0,18'h0};//临时粗略将18'h1FFFF视为1
//第1组插值核
localparam [17:0] group1_coe[7:0] = {18'h3EFC2,18'h017FB,18'h3D238,18'h1F79E,18'h037F5,18'h3E57F,18'h0115D,18'h3F317};
//第2组插值核
localparam [17:0] group2_coe[7:0] = {18'h3E211,18'h02B8A,18'h3B02C,18'h1DEF8,18'h077BE,18'h3CAC8,18'h02236,18'h3E6CB};
//第3组插值核
localparam [17:0] group3_coe[7:0] = {18'h3D80C,18'h03953,18'h39A94,18'h1B77F,18'h0BC5B,18'h3B272,18'h030D5,18'h3DC5E};
//第4组插值核
localparam [17:0] group4_coe[7:0] = {18'h3D26A,18'h04095,18'h3914A,18'h1837E,18'h10254,18'h39F21,18'h03B9D,18'h3D4F2};
//第5组插值核
localparam [17:0] group5_coe[7:0] = {18'h3D170,18'h04130,18'h3935A,18'h145F3,18'h145F3,18'h3935A,18'h04130,18'h3D170};
//第6组插值核
localparam [17:0] group6_coe[7:0] = {18'h3D4F2,18'h03B9D,18'h39F21,18'h10254,18'h1837E,18'h3914A,18'h04095,18'h3D26A};
//第7组插值核
localparam [17:0] group7_coe[7:0] = {18'h3DC5E,18'h030D5,18'h3B272,18'h0BC5B,18'h1B77F,18'h39A94,18'h03953,18'h3D80C};
//第8组插值核
localparam [17:0] group8_coe[7:0] = {18'h3E6CB,18'h02236,18'h3CAC8,18'h077BE,18'h1DEF8,18'h3B02C,18'h02B8A,18'h3E211};
//第9组插值核
localparam [17:0] group9_coe[7:0] = {18'h3F317,18'h0115D,18'h3E57F,18'h037F5,18'h1F79E,18'h3D238,18'h017FB,18'h3EFC2};
reg [17:0] sinc_coe [7:0];//对应插值点使用的插值核
reg [3:0] sinc_cnt = 0;//插值计数,0时为原始点,1~9为插值点,其余数值保留
reg [7:0] samp_data [7:0];//每次从RAM读取数据时进行锁存更新
//8个乘法结果
reg [25:0] mult_data[7:0];
assign disc_rd = (sinc_cnt == 4'd8) ? 1'b1:1'b0; //插值第8个点时,读取新的数据
//插值倍数10,插值点计数
always@(posedge clk)
begin
if(sinc_en == 1'b1) begin
if(sinc_cnt == 4'd9)
sinc_cnt <= 4'd0;
else
sinc_cnt <= sinc_cnt + 1;
end
else
sinc_cnt <= 4'd0;
end
//原始点锁存
always@(posedge clk)
begin
if(sinc_en == 1'b1 && sinc_cnt == 4'd0) begin //插值使能
samp_data[0] <= disc_samp;//新输入的点
samp_data[1] <= samp_data[0];
samp_data[2] <= samp_data[1];
samp_data[3] <= samp_data[2];
samp_data[4] <= samp_data[3];
samp_data[5] <= samp_data[4];
samp_data[6] <= samp_data[5];
samp_data[7] <= samp_data[6];
end
end
//插值核系数选择
always@(posedge clk)
begin
case(sinc_cnt)
4'd0:sinc_coe <= group0_coe;//原始点系数
4'd1:sinc_coe <= group1_coe;//第1个插值点系数
4'd2:sinc_coe <= group2_coe;//第2个插值点系数
4'd3:sinc_coe <= group3_coe;//第3个插值点系数
4'd4:sinc_coe <= group4_coe;//第4个插值点系数
4'd5:sinc_coe <= group5_coe;//第5个插值点系数
4'd6:sinc_coe <= group6_coe;//第6个插值点系数
4'd7:sinc_coe <= group7_coe;//第7个插值点系数
4'd8:sinc_coe <= group8_coe;//第8个插值点系数
4'd9:sinc_coe <= group9_coe;//第9个插值点系数
default:;
endcase
end
//乘法器0
mult_gen mult_gen_0 (
.CLK(clk), // input wire CLK
.A(samp_data[0]), // input wire [7 : 0] A
.B(sinc_coe[0]), // input wire [17 : 0] B
.P(mult_data[0]) // output wire [25 : 0] P
);
//乘法器1
mult_gen mult_gen_1 (
.CLK(clk), // input wire CLK
.A(samp_data[1]), // input wire [7 : 0] A
.B(sinc_coe[1]), // input wire [17 : 0] B
.P(mult_data[1]) // output wire [25 : 0] P
);
//乘法器2
mult_gen mult_gen_2 (
.CLK(clk), // input wire CLK
.A(samp_data[2]), // input wire [7 : 0] A
.B(sinc_coe[2]), // input wire [17 : 0] B
.P(mult_data[2]) // output wire [25 : 0] P
);
//乘法器3
mult_gen mult_gen_3 (
.CLK(clk), // input wire CLK
.A(samp_data[3]), // input wire [7 : 0] A
.B(sinc_coe[3]), // input wire [17 : 0] B
.P(mult_data[3]) // output wire [25 : 0] P
);
//乘法器4
mult_gen mult_gen_4 (
.CLK(clk), // input wire CLK
.A(samp_data[4]), // input wire [7 : 0] A
.B(sinc_coe[4]), // input wire [17 : 0] B
.P(mult_data[4]) // output wire [25 : 0] P
);
//乘法器5
mult_gen mult_gen_5 (
.CLK(clk), // input wire CLK
.A(samp_data[5]), // input wire [7 : 0] A
.B(sinc_coe[5]), // input wire [17 : 0] B
.P(mult_data[5]) // output wire [25 : 0] P
);
//乘法器6
mult_gen mult_gen_6 (
.CLK(clk), // input wire CLK
.A(samp_data[6]), // input wire [7 : 0] A
.B(sinc_coe[6]), // input wire [17 : 0] B
.P(mult_data[6]) // output wire [25 : 0] P
);
//乘法器7
mult_gen mult_gen_7 (
.CLK(clk), // input wire CLK
.A(samp_data[7]), // input wire [7 : 0] A
.B(sinc_coe[7]), // input wire [17 : 0] B
.P(mult_data[7]) // output wire [25 : 0] P
);
//使用加法器实现有符号数相加
//二点相加
wire [25:0] add2_0;
wire [25:0] add2_1;
wire [25:0] add2_2;
wire [25:0] add2_3;
adder2 adder2_inst0 (
.A(mult_data[0]), // input wire [25 : 0] A
.B(mult_data[1]), // input wire [25 : 0] B
.CLK(clk), // input wire CLK
.S(add2_0) // output wire [26 : 0] S
);
adder2 adder2_inst1 (
.A(mult_data[2]), // input wire [25 : 0] A
.B(mult_data[3]), // input wire [25 : 0] B
.CLK(clk), // input wire CLK
.S(add2_1) // output wire [26 : 0] S
);
adder2 adder2_inst2 (
.A(mult_data[4]), // input wire [25 : 0] A
.B(mult_data[5]), // input wire [25 : 0] B
.CLK(clk), // input wire CLK
.S(add2_2) // output wire [26 : 0] S
);
adder2 adder2_inst3 (
.A(mult_data[5]), // input wire [25 : 0] A
.B(mult_data[6]), // input wire [25 : 0] B
.CLK(clk), // input wire CLK
.S(add2_3) // output wire [26 : 0] S
);
//四点相加
reg [25:0] add4_0;
reg [25:0] add4_1;
adder4 adder4_inst0 (
.A(add2_0), // input wire [26 : 0] A
.B(add2_1), // input wire [26 : 0] B
.CLK(clk), // input wire CLK
.S(add4_0) // output wire [27 : 0] S
);
adder4 adder4_inst1 (
.A(add2_2), // input wire [26 : 0] A
.B(add2_3), // input wire [26 : 0] B
.CLK(clk), // input wire CLK
.S(add4_1) // output wire [27 : 0] S
);
//八点相加
wire [25:0] add8;
adder8 adder8 (
.A(add4_0), // input wire [26 : 0] A
.B(add4_1), // input wire [26 : 0] B
.CLK(clk), // input wire CLK
.S(add8) // output wire [27 : 0] S
);
assign sinc_valid = 1'b1;
assign sinc_data = add8[25:18];
endmodule
编写testbench,对插值模块进行仿真验证,testbench代码如下:
module testbench(
);
reg clk = 0; //100M时钟
always
begin
# 5
clk <= ~clk;
end
wire disc_rd;//采样点有效标志
wire [7:0] disc_samp; //离散采样点输出
disc_samp_gen disc_samp_gen(
.clk(clk),
.disc_rd(disc_rd),//采样点有效标志
.disc_samp(disc_samp)//离散采样点输出
);
sinc_process sinc_process(
.clk(clk),
.sinc_en(1'b1),
.disc_rd(disc_rd),//采样点有效标志
.disc_samp(disc_samp),//离散采样点输出
.sinc_valid(),//插值数据有效标志
.sinc_data()//插值后数据
);
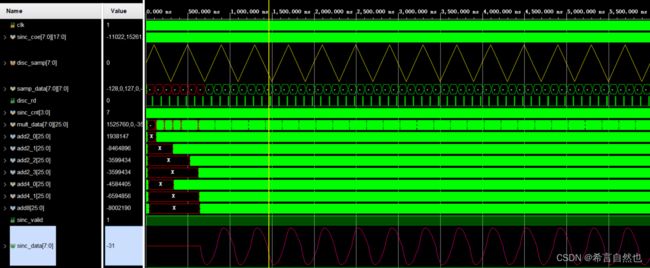
endmodule仿真验证结果如下:
可以看到,图中黄色部分为原始采样点的直线连接波形,紫色部分为正弦插值后的波形。正弦插值仿真成功。
vivado工程以及学习sinc插值的过程文件(主要是为了存档,方便后续自己使用):https://download.csdn.net/download/yindq1220/87557975?spm=1001.2014.3001.5501