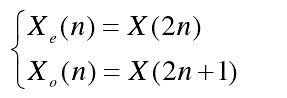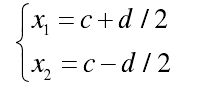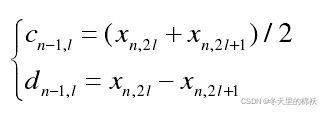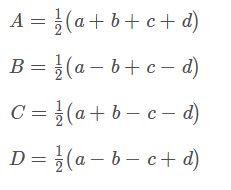Haar小波提升算法

传统的小波变换是在傅里叶变换的基础上演变而来，计算过程中存在着大量的卷积运算或是乘累加的计算，如若在硬件上实现，势必会消耗大量的寄存器资源，而且速度也上不去。提升小波又称为第二代小波，最早是由 Sweldens W.博士于 1995 年在贝尔实验室提出，相对于 Mallat 算法而言，提升小波抛弃了原有的傅里叶变换思想，可在时域中完成正交小波的构造，具有算法简单、运算速度快、占用内存少等优点，而且还能实现整数到整数小波变换，这对于硬件上实现小波变换来说无疑是个天大的好消息。

小波变换的提升算法主要由分裂（Split）、预测（Prediction）和更新（Update）三个部分构成。分裂是将一个信号分裂成两个信号，预测主要作用是消除第一步分裂之后所留下的数据冗余，更新则是起到一个修正数据的作用。下面将讨论每一步的具体实现过程。

      1）分裂：分裂是将原始信号 X(n) 分裂成两个集合：Xe(n) 和Xo(n) 。最常用的分裂方法是惰性分裂，即对信号 X(n) 进行奇偶采样，其中偶采样构成集合Xe(n) ，奇采样构成集合Xo(n) ，即：

相反地，可以通过 X e(n) 和 X o(n) 来恢复信号 X(n) 。

2）预测：由于Xe(n) 和Xo(n) 都是通过对信号 X(n) 进行采样得到的，所以Xe(n) 和Xo(n) 之间必定存在着高度的相关性。因此，可以利用其中一个集合来预测另一个集合。通常习惯就是利用偶子集 Xe(n) 来预测奇子集Xo(n) ，其
预测误差定义为：

 等式中的 P(Xe(n))为预测算子。通常采用多项式插值作为预测算子，当确定预测算子之后，便可以通过偶子集 Xe(n) 和预测误差 d(n) 来恢复奇子集Xo(n) ，进而可以恢复原始信号 X(n) ，

由于预测误差 d(n) 表示原始信号 X(n) 局部区域的低频分量误差，故预测误差 d(n) 可看作是信号的高频分量。

3）更新：低频信号保留了原始信号的绝大部信息，为了使其更逼近原始信号的整体特征（如均值等），确保整体特性和原始信号相同，则需要一个更新过程，来对数据进行修正，其过程如下：

其中U() 为更新算子。

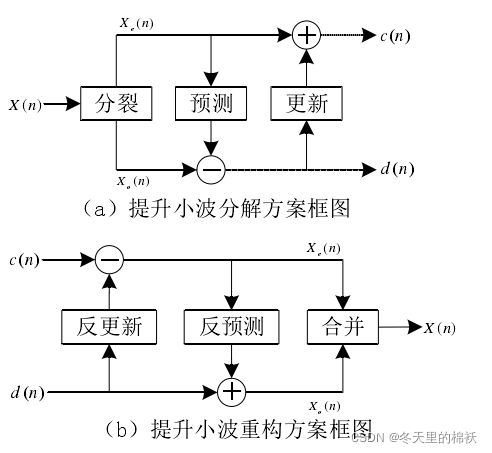
 提升小波的分解与重构示意图。信号 X(n) 首先分裂成Xe(n) 和 Xo(n) 两个信号，然后用 Xe(n)对Xo(n)进行预测，得到预测误差 d(n) ，最后用预测误差 d(n) 来更新信号 Xe(n) ，从而获得进行信号 c(n) 。重构过程则与之相反

Haar 小波变换的提升算法:

本小节将介绍 Haar 小波的提升算法及其原位计算，即在不新增内存的情况下实现小波变换。
  定义x1和x2 两个数，其低频近似系数 c 和高频细节系数 d 分别为：

 则{x1, x2} 的 Haar 小波变换结果为 {c, d}。其逆变换恢复x1 、x2 的公式为：

若对于长度为 2n的信号,则其变换结果为：

多级 Haar 小波变换的分解与重构的过程:

为了实现原位计算，可先计算出细节系数 d ，并将结果 d 存放在原x2 的位置上，接着用x1和 d 的值计算近似系数 c 的值最后将 c 存放在x1 的位置上。内存数据的变化过程。

同理，可利用逆变换实现原位数据恢复。  

      小波指的是一种能量在时域非常集中的波，它的能量有限，都集中在某一点附近，而且积分的值为零，这说明它与傅里叶波一样是正交波。

      图像的傅里叶变换是将图像信号分解为各种不同频率的正弦波。同样，小波变换是将图像信号分解为由原始小波位移和缩放之后的一组小波。小波在图像处理里被称为图像显微镜，原因在于它的多分辨率分解能力可以将图片信息一层一层分解剥离开来。剥离的手段就是通过低通和高通滤波器。

       小波变换可以和傅里叶变换结合起来理解。傅里叶变换是用一系列不同频率的正余弦函数去分解原函数，变换后得到是原函数在正余弦不同频率下的系数。小波变换使用一系列的不同尺度的小波去分解原函数，变换后得到的是原函数在不同尺度小波下的系数。不同的小波通过平移与尺度变换分解，平移是为了得到原函数的时间特性，尺度变换是为了得到原函数的频率特性。

小波变换步骤：

1.把小波w(t)和原函数f(t)的开始部分进行比较，计算系数C。系数C表示该部分函数与小波的相似程度。

2.把小波向右移k单位，得到小波w(t-k)，重复1。重复该步骤直至函数f结束.

3.扩展小波w(t)，得到小波w(t/2)，重复步骤1,2.

4.不断扩展小波，重复1,2,3.

我这里使用的haar小波，缩放函数是[1 1]，小波函数是[1 -1]。是最简单的小波了。

假设一张图片只有4个像素，其经过2-D DWT之后得到4张子图，每个子图的详细计算过程如下：
在这里插入图片描述

        图像可以看作是一组二维数据，而 Haar 提升小波变换是一维变换，为了实现图像的二维变换，可通过对行和列分别进行变换来达到二维变换的目的。图像数据进来时，首先进行行变换，变换结果按照树状结果存储到SDRAM 中，图像的一行数据变换结果也存储在同一行，近似系数存放在前，
细节系数存放在后，如图 4-6 所示。列变换在行变换结束后进行，依次从SDRAM 中读出每一列的数据进行变换，并将同一列的变换结果存储在一列中，近似系数在前，细节系数在后。

 

Haar 提升小波变换的 FPGA 实现

图像小波变换主要分为行变换和列变换，而行变换与列变换之间唯一不同是读取数据的方向不一样，其计算过程都是相同的。在处理方式上，对于第一次行变换可直接时时处理，即对于刚输入的数据可直接进行变换。而对于后续的变换则需要先从 SDRAM 中读取数据再做变换处理。
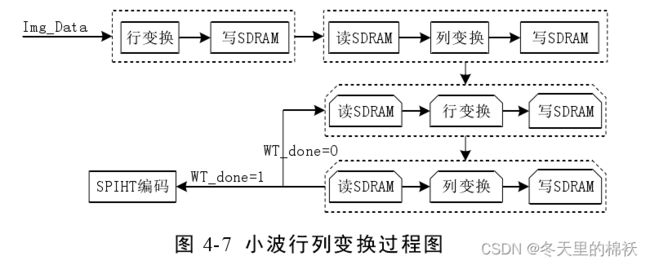
  图 4-7 给出了小波行列变换的过程示意图，图像数据进来直接进行变换，同时将变换结果写入 SDRAM。行变化完成过后紧接着进行列变换处理。在列变换的过程中，需要先从 SDRAM 读取行变换的结果，再进行计算，同时将计算结果存入 SDRAM 中。为了防止数据覆盖，需要把 SDRAM 划分成两个存储模块，一个存储上一次的计算结果，另一个存储当前计算结果。在下一次进行变换时，读取上一次行列变换之后的低频数据进变换，高频数据不动。分别经过三次行列变换之后，就完成了图像的三层小波分解。

Haar 提升小波变换原理框图如图 4-8 所示，数据进来先做一个缓存，当下一次数据进来时，则同时进行求和、求差运算，之后再将求和之后的结果右移一位，获得变换后的近似系数。为了保证结果的同步性，将求差之后的结果延时一个时钟，这样就可以同时获得变换之后的近似系数和细节系数。

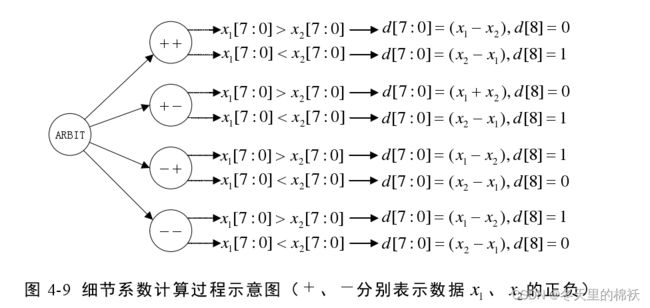
为了确保后续的编码过程正确，变换之后的数据位仍然表示当前数据绝对值的大小，在数据位前增加一位符号标记位。在计算时，先判断数据符号位，然后再进行计算。这样一来，数据位宽就变成了 9 位，最高位是符号位，表示数据的正负，低八位为数据位，表示数据的大小。图 4-9 给出了细节系数的计算过程，图中 + 和 -分别表示数据x1 、x2 的正负，最高位 0 为正数，1为负数。

 基于小波变换的图像压缩及其 FPGA 实现-游斌相
https://blog.csdn.net/baidu_27643275/article/details/84826773

https://blog.csdn.net/qq_30815237/article/details/89704855