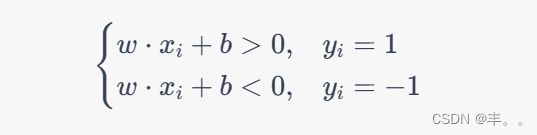感知器算法
感知器算法原理说明
感知器是一种二分类的线性分类算法,其原理基于神经元的工作原理。感知器将输入数据通过加权求和的方式映射到一个输出,然后根据输出的结果进行分类。
具体来说,给定一个训练集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) D={(x_1,y_1),(x_2,y_2),...,(x_n,y_n)} D=(x1,y1),(x2,y2),...,(xn,yn),其中 x i x_i xi 是一个 m m m 维向量,表示第 i i i 个样本的特征, y i ∈ − 1 , 1 y_i\in {-1,1} yi∈−1,1 是该样本的标签。感知器的目标是找到一个权重向量 w w w,使得对于所有样本 ( x i , y i ) (x_i,y_i) (xi,yi),有:
其中 w ⋅ x i w\cdot x_i w⋅xi 表示 w w w 和 x i x_i xi 的内积, b b b 是一个常数,称为偏置项。上述式子可以简化为:
y i ( w ⋅ x i + b ) > 0 y_i(w\cdot x_i+b)>0 yi(w⋅xi+b)>0
即对于正确分类的样本,其预测值与真实值之积大于零。
感知器的训练过程是一个迭代的过程,每次迭代通过更新权重向量 w w w 和偏置项 b b b 来逐步提高模型的准确率。具体来说,在每一轮迭代中,从训练集中选取一个错分类的样本 ( x i , y i ) (x_i,y_i) (xi,yi),然后按以下公式更新 w w w 和 b b b:
w = w + η y i x i w=w+\eta y_ix_i w=w+ηyixi
b = b + η y i b=b+\eta y_i b=b+ηyi
其中 η \eta η 是学习率,控制着每次更新的步长。这个过程会一直重复,直到所有样本都被正确分类或达到预设的迭代次数。
需要注意的是,感知器算法只能处理线性可分的数据集。如果数据集不是线性可分的,算法会一直迭代下去而无法停止。此外,感知器还存在多个权重向量和偏置项的解,因此不同的初始权重和偏置可能会导致不同的结果。
感知器算法公式推导
感知器算法的公式推导可以从定义开始,假设我们有一个二分类的数据集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) D={(x_1,y_1),(x_2,y_2),...,(x_n,y_n)} D=(x1,y1),(x2,y2),...,(xn,yn),其中 x i x_i xi 是一个 m m m 维向量,表示第 i i i 个样本的特征, y i ∈ − 1 , 1 y_i\in {-1,1} yi∈−1,1 是该样本的标签。我们的目标是找到一个超平面 w ⋅ x + b = 0 w\cdot x+b=0 w⋅x+b=0 将数据集分为两类。
假设我们已经得到了一个权重向量 w w w 和偏置项 b b b,我们可以将其代入超平面方程中,得到样本 x i x_i xi 距离超平面的距离:
∣ w ⋅ x i + b ∣ ∣ w ∣ \frac{|w\cdot x_i+b|}{|w|} ∣w∣∣w⋅xi+b∣
其中 ∣ w ∣ |w| ∣w∣ 表示向量 w w w 的模长。我们希望距离正确分类的样本越远越好,因此可以定义感知器的损失函数为:
L ( w , b ) = − ∑ x i ∈ M y i ( w ⋅ x i + b ) L(w,b)=-\sum_{x_i\in M}y_i(w\cdot x_i+b) L(w,b)=−xi∈M∑yi(w⋅xi+b)
其中 M M M 是被错误分类的样本集合。对于正确分类的样本, y i ( w ⋅ x i + b ) > 0 y_i(w\cdot x_i+b)>0 yi(w⋅xi+b)>0,所以损失函数取值为负数。而对于错误分类的样本, y i ( w ⋅ x i + b ) < 0 y_i(w\cdot x_i+b)<0 yi(w⋅xi+b)<0,损失函数取值为正数。我们的目标是最小化损失函数,使得所有样本都被正确分类。
接下来,我们使用随机梯度下降算法来优化损失函数。在每次迭代中,我们随机选择一个错误分类的样本 ( x i , y i ) (x_i,y_i) (xi,yi),然后按照以下公式更新 w w w 和 b b b:
w = w + η y i x i w=w+\eta y_ix_i w=w+ηyixi
b = b + η y i b=b+\eta y_i b=b+ηyi
其中 η \eta η 是学习率,控制着每次更新的步长。这个过程会一直重复,直到所有样本都被正确分类或达到预设的迭代次数。
可以证明,如果数据集是线性可分的,那么感知器算法一定会收敛,得到一个能够将数据集分为两类的超平面。但如果数据集不是线性可分的,算法会一直迭代下去而无法停止。此外,感知器还存在多个权重向量和偏置项的解,因此不同的初始权重和偏置可能会导致不同的结果。
下面我们来推导感知器算法的更新公式。首先定义一个样本点 ( x i , y i ) (x_i, y_i) (xi,yi) 的损失函数为:
L i ( w , b ) = − y i ( w ⋅ x i + b ) L_i(w,b)=-y_i(w\cdot x_i+b) Li(w,b)=−yi(w⋅xi+b)
如果这个样本点被正确分类,即 y i ( w ⋅ x i + b ) > 0 y_i(w\cdot x_i+b)>0 yi(w⋅xi+b)>0,那么这个样本点的损失函数为0。如果这个样本点被错误分类,即 y i ( w ⋅ x i + b ) ≤ 0 y_i(w\cdot x_i+b)\leq 0 yi(w⋅xi+b)≤0,那么这个样本点的损失函数就是 − y i ( w ⋅ x i + b ) -y_i(w\cdot x_i+b) −yi(w⋅xi+b)。
为了最小化感知器的损失函数,我们需要对所有被错误分类的样本点 ( x i , y i ) (x_i, y_i) (xi,yi) 更新权重 w w w 和偏置 b b b。假设当前迭代到第 t t t 次,我们选取的样本点为 ( x i , y i ) (x_i, y_i) (xi,yi),那么在这次迭代中,我们需要将 w w w 和 b b b 更新为:
w t + 1 = w t + η y i x i w_{t+1} = w_t + \eta y_i x_i wt+1=wt+ηyixi
b t + 1 = b t + η y i b_{t+1} = b_t + \eta y_i bt+1=bt+ηyi
其中, η \eta η 是学习率, w t w_t wt 和 b t b_t bt 是上一次迭代得到的权重和偏置。这个更新规则的含义是:如果一个样本点 ( x i , y i ) (x_i, y_i) (xi,yi) 被错误分类,那么我们就沿着它的负梯度方向更新权重和偏置,使得这个样本点离超平面更近,从而使得它被正确分类。
在实际应用中,感知器算法往往需要多次迭代才能得到较好的结果。我们可以设置一个最大迭代次数或者一个阈值,当达到这个条件时就停止迭代。在每次迭代中,我们可以随机选取一个错误分类的样本点来更新权重和偏置,或者按照顺序遍历所有的样本点来更新权重和偏置。无论是哪种更新方式,最终的结果都是将数据集分为两类的超平面。