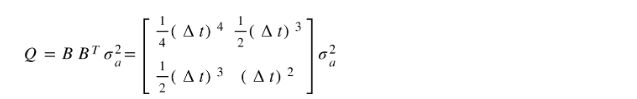卡尔曼滤波滤波方程
Before getting into what a Kalman filter is or what it does, let’s first do an exercise. Open the google maps application on your phone and check your device’s current location.
在了解什么是卡尔曼滤波器或其功能之前,我们先做一个练习。 在手机上打开Google Maps应用程序,然后检查设备的当前位置。
Did you check it? How accurately is it able to pinpoint your location? Quite accurately isn’t it. The errors from your actual location might range from 2m to 20m depending on the quality of the GPS or whether you are indoors or outdoors but still, it did a pretty good job. In fact, it did a great job considering the fact that earth is so huge and it’s able to pinpoint your location, with a small error radius which is represented by a circle around the point.
你检查了吗? 能够精确定位您的位置吗? 完全是不是。 根据GPS的质量,或者您是在室内还是室外,实际位置的误差范围可能在2m至20m之间,但这仍然做得很好。 实际上,考虑到地球是如此之大,它能够以较小的误差半径(通过围绕该点的圆圈表示)来精确定位您的位置,因此,它做得很好。
But now let’s say you install a GPS on your car and you are told to remote control it from your house, given the feed from the GPS. Would you be able to navigate your car through the streets? Your answer would be definitely no. Even though the GPS is able to pinpoint the location of your car with decent accuracy, the error in measurements can range from 2 to 3 meters which makes it impossible to drive with no other feed. This is where the field of localization comes in. Localization is the task of reducing the error in the position of our vehicle to cm level accuracy.
但是,现在让我们假设您在汽车上安装了GPS,然后根据GPS的提示,您被告知要在家中对其进行遥控。 您能在街上开车吗? 您的答案肯定不会。 即使GPS能够精确定位您的汽车位置,但测量误差可能会在2至3米的范围内,这使得没有其他饲料就无法驾驶。 这就是本地化的领域。本地化是将我们的车辆位置误差降低到厘米级精度的任务。
Now to do this, instead of just relying on our GPS, we install other instruments such as IMU, camera, lidar, and radar to our vehicle and use the additional information to get a better understanding of the environment.
现在,不仅要依靠我们的GPS,还需要在车辆上安装其他仪器,例如IMU,摄像头,激光雷达和雷达,并使用其他信息来更好地了解环境。
Ok, so now we have a much detailed sense of the environment and, if now the task is given to you, you’ll probably feel more confident in being able to navigate the car through the streets with just the device feeds. At Least the less crowded ones. But what if this task is given to a computer? Humans are quite good at recognizing patterns without much effort but, for a computer, it still needs to process the information, and factors like measurement error, measurement noise, process error, and delays add further complexity. Here’s where Kalman filter comes in.
好的,现在我们对环境有了更详尽的了解,如果现在将任务交给您,您可能会感到更加自信,能够仅使用设备提要在街上驾驶汽车。 至少不那么拥挤。 但是,如果将此任务交给计算机怎么办? 人类非常擅长于识别模式,而无需花费太多精力,但对于计算机而言,它仍然需要处理信息,并且诸如测量误差,测量噪声,过程误差和延迟之类的因素会进一步增加复杂性。 这就是卡尔曼滤波器的作用。
Kalman filter is an algorithm, named after Rudolf E. Kálmán, one of the primary developers of this theory, which is extensively used for many applications. A common application is for Guidance, Navigation, and Control of Vehicles.
卡尔曼滤波器是一种算法,以该理论的主要开发者之一Rudolf E.Kálmán命名,已广泛用于许多应用程序。 常见的应用是车辆的制导,导航和控制。
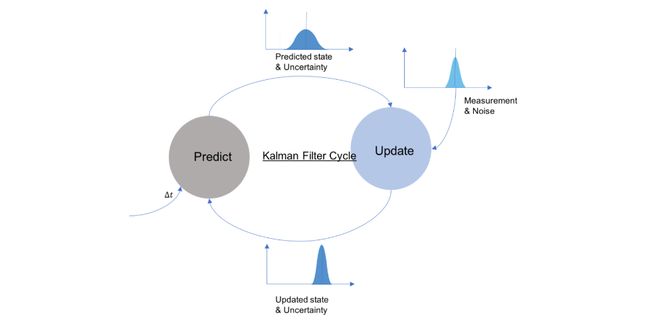
Kalman filters are based on the theory of Bayesian probabilities. There are typically two steps in the Kalman filter: Predict and Update.
卡尔曼滤波器基于贝叶斯概率理论。 卡尔曼滤波器通常有两个步骤: Predict和Update 。
Stages of Kalman Filter 卡尔曼滤波的阶段To understand what each of the steps does, we first define something called the State of the vehicle. The state represents a collection of measurements that we would like to describe our vehicle with. It can be a combination of anything from, position, velocity, lateral acceleration, yaw, yaw rate, and many more. Let’s take a simple example of a car that can only move along the x-axis with only the position as part of the state. We start with a good guess for the state of the vehicle.
为了了解每个步骤的作用,我们首先定义一个称为“车辆状态 ”的内容。 状态代表我们要用来描述车辆的测量值的集合。 它可以是位置,速度,横向加速度,偏航,偏航率等等中任何一项的组合。 让我们举一个简单的汽车示例,该汽车只能沿x轴移动,而位置仅是状态的一部分。 我们首先对车辆的状态进行猜测。
Let’s start with position 0 m. We assume a constant velocity model i.e., we will not consider the effect of acceleration to our vehicle’s position estimate.
让我们从位置0 m开始。 我们假设一个恒定速度模型,即,我们将不考虑加速度对我们的车辆位置估计的影响。
Now we bump up the velocity of our vehicle to 1 m/s. Remember that we have assumed a constant velocity model, so we will not consider the acceleration in between. Where do you expect the vehicle to be after 1second has elapsed? You probably answered it correctly. The answer is at 1m. The velocity of the vehicle is 1 m/s and according to distance = velocity * time, we get distance as 1m.
现在,我们将车辆的速度提高到1 m / s。 请记住,我们假设了一个恒定速度模型,因此我们将不考虑两者之间的加速度。 您希望车辆经过1秒后会在哪里? 您可能回答正确。 答案是1m。 车辆的速度为1 m / s,根据距离=速度*时间,我们得出距离为1m。
Now, can you predict the position after 2 more seconds have elapsed with the same velocity? The answer is 3m. Easy, right? Given the velocity of the vehicle at all times, you were able to predict the position of the vehicle. If we were able to predict the position of the vehicle without any hustle, why do we need Kalman filter?
现在,您能以相同的速度经过2秒后预测位置吗? 答案是3m。 容易吧? 给定车辆始终的速度,您就可以预测车辆的位置。 如果我们能够毫无障碍地预测车辆的位置,为什么我们需要卡尔曼滤波器?
The truth is, we wouldn’t have needed Kalman filters if we could have been 100% sure of all our measurements. But in reality, no measurement is perfect. So the place where we assume our velocity to be 1 m/s may not be 100% accurate. It may be 0.9 m/s or 1.1 m/s or something else, we aren’t sure. There is always some margin for error. Now, what will happen to our position estimate? Because there is an error term in velocity, there will also be an associated error term for the position estimate as well. As the vehicle moves with time, we can propagate the state of the vehicle along with it’s associated error term. This is the prediction step of the Kalman filter.
事实是,如果我们可以100%确信所有测量结果,就不需要卡尔曼滤波器。 但实际上,没有任何测量是完美的。 因此,我们假设速度为1 m / s的地方可能不是100%准确的。 我们不确定这可能是0.9 m / s或1.1 m / s或其他。 总会有一些误差。 现在,我们的职位估计会怎样? 由于速度中存在误差项,因此位置估计也将具有关联的误差项。 随着车辆随时间移动,我们可以传播车辆状态及其相关的误差项。 这是卡尔曼滤波器的预测步骤。
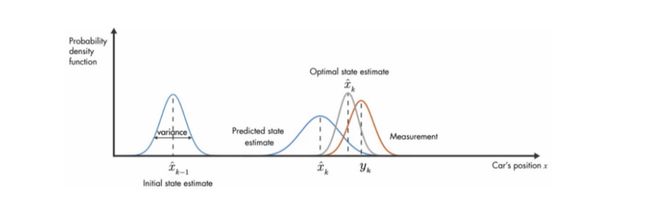
Propagation of car’s state 汽车状态的传播Now the prediction step alone cannot solve the problem of localization as the errors will keep accumulating with time, degrading our position estimate. Our estimates degrade with time because no new information is collected while the car is moving and hence some information is lost during each propagation step. This is evident from the image above where the probability distribution of position estimate gets wider as it moves ahead. And, if this is continued, the probability distribution of the vehicle position will tend to uniform distribution.
现在,仅凭预测步骤就无法解决定位问题,因为误差会随着时间的推移而不断累积,从而降低了我们的位置估算值。 我们的估计会随着时间的推移而降低,因为在汽车行驶时没有收集到任何新信息,因此在每个传播步骤中都会丢失一些信息。 从上图可以清楚地看出,位置估计的概率分布随着向前移动而变宽。 并且,如果继续这样,则车辆位置的概率分布将趋于均匀分布。
The Update step solves this problem. Let’s say we have a GPS installed on our vehicle which tells us our position every 2 seconds. So after every 2 seconds, using this new information, we can update the state of the vehicle based on the measurements and previous belief of the state. The update step makes sure that the errors don’t keep accumulating with time.
更新步骤解决了此问题。 假设我们在车辆上安装了GPS,每2秒就会告诉我们我们的位置。 因此,每隔2秒钟,使用此新信息,我们就可以基于测量结果和状态的先前信念来更新车辆的状态。 更新步骤可确保错误不会随着时间累积。
卡尔曼滤波方程 (Kalman Filter equations)
Cool, if you have understood everything, you have got a good grasp of what Kalman filters are, and how they work. So, let’s see how all this is implemented in mathematical equations.
太好了,如果您了解了所有内容,那么您将对Kalman过滤器及其工作原理有很好的了解。 因此,让我们看看如何在数学方程式中实现所有这些功能。
Predict:
预测:
Update:
更新:
Did I suddenly confuse you with all the equations? Don’t worry, even I felt the same way when I had faced these equations for the first time. Instead of getting too deep into the linear algebra that is making this possible, we will try to understand the essence of each equation. You can still follow the equations without getting into the derivation of the advanced linear algebra concepts.
我突然把所有方程式弄糊涂了吗? 不用担心,即使是我第一次面对这些方程式时,也有同样的感觉。 我们将不会试图深入了解每个方程式的实质,而不必太过深入地研究线性代数使之成为可能。 您仍然可以遵循这些方程式,而无需进行高级线性代数概念的推导。
Consider an example of a car initially at position 0. We measure its position every Δt seconds and we keep track of the car’s position and velocity along the x- dimension.
考虑一个最初在位置0处的汽车的示例。我们每隔Δt秒测量一次它的位置,并沿x维度跟踪汽车的位置和速度。
步骤1 :(预测) (Step 1: (Predict))
1.1 Propagation of State:
1.1国家的传播:
As we are describing our car using position and velocity, these quantities will be part of the car’s state. x is the position and ẋ is the derivative of position wrt to time which is velocity.
当我们使用位置和速度描述汽车时,这些量将成为汽车状态的一部分。 x是位置, ẋ是位置wrt对时间的导数,即速度。
Control inputs represent the collection of external parameters that are used to control the car. In our case, we consider lateral acceleration ‘a’ as an input.
控制输入代表用于控制汽车的外部参数的集合。 在我们的案例中,我们将横向加速度“ a”视为输入。
The state-transition model describes how the car’s state propagates in the time, given the state of the previous time step. The propagation of state is governed by the two equations below:
状态转换模型描述了给定上一个时间步长的状态下汽车状态在时间中的传播方式。 状态的传播受以下两个方程式控制:
The multiplication F(k) X(k-1) is translated by the above equations. Here the subscript k of F has no significance because F does not vary with time.
乘积F(k)X(k-1)由上述方程式转换。 在此, F的下标k不重要,因为F不会随时间变化。
The control-input model is a matrix that defines the effect of control-inputs on the car’s state. For only lateral acceleration as the input, its effect on the state parameters are as follows:
控制输入模型是一个矩阵,用于定义控制输入对汽车状态的影响。 仅将横向加速度作为输入,它对状态参数的影响如下:
The equations above are what you will get on the multiplication B(k) u(k). Similar to F, the subscript k of B also does not have any significance as B is also constant throughout.
上面的等式是乘法B(k)u(k)的结果 。 与F相似, B的下标k也没有任何意义,因为B始终是恒定的。
You might wonder what the hat in X̂ (k|k-1) means? In linear algebra to represent an estimate of a variable, we put a hat over the variable. As we can only estimate the state of the car is, the hat represents that it is an estimate of the state.
您可能想知道X̂(k | k-1)中的帽子是什么意思? 在线性代数中,代表变量的估计,我们在变量上加了一个帽子。 因为我们只能估计汽车的状态,所以帽子代表它是状态的估计。
1.2 Propagation of Estimate Covariance Matrix:
1.2估计协方差矩阵的传播:
P(k) represents the estimate covariance matrix of the uncertainty in the state parameters i.e. position and velocity. It keeps track of the errors associated with our state. The subscript k|k-1 represents the estimate covariance at time step k given the estimate covariance at time step k-1. It is initialized with some prior variance.
P(k)表示状态参数(即位置和速度)中不确定性的估计协方差矩阵。 它跟踪与我们的状态相关的错误。 下标k | k-1表示给定时间步长k-1的估计协方差时,时间步长k的估计协方差。 初始化时有一些先验差异。
Because we have two parameters in our state, the estimate covariance matrix is 2 x 2 matrix. We initialize the matrix based on our initial beliefs of the uncertainty in position and velocity. These values occupy the major diagonal of the matrix in the same order as that of the order in the state. When there is no measurement available, the estimate covariance matrix is propagated based on the state-transition model F with Q as the process noise. Q is calculated as follows:
因为我们在状态中有两个参数,所以估计协方差矩阵为2 x 2矩阵。 我们基于对位置和速度不确定性的最初信念初始化矩阵。 这些值以与状态中顺序相同的顺序占据矩阵的主要对角线。 当没有可用的度量时,基于状态转换模型F传播估计协方差矩阵,其中Q为过程噪声。 Q计算如下:
Keep in mind the uncertainty of the state parameters will increase in this step because of the propagation step.
请记住,由于传播步骤,状态参数的不确定性将在此步骤中增加。
步骤2 :(更新) (Step 2: (Update))
2.1 Measurement:
2.1测量
Measurement step also known as the Innovation step is the step where we gain information from the instruments installed on the car. This is a crucial step as, without any external information, the car is as good as blind.
测量步骤也称为创新步骤,是我们从汽车上安装的仪器中获取信息的步骤。 这是至关重要的一步,因为在没有任何外部信息的情况下,汽车就像盲人一样好。
In our case, we will assume a GPS-like system on our car, that can tell the position of the car periodically.
在我们的案例中,我们将在汽车上假设一个类似GPS的系统,该系统可以定期告诉汽车位置。
You can call the observation model a matrix, that transforms our state to the format of that of the measurement matrix z(k). In our case, we only use GPS to measure the position so,
您可以将观测模型称为矩阵,该矩阵将我们的状态转换为测量矩阵z(k)的格式。 在我们的案例中,我们仅使用GPS来测量位置,
Hence, the observation model in our case will be:
因此,在我们的案例中,观察模型将是:
Again, we can drop the subscript k as it is time-invariant. On multiplying observation model with the state, we get:
同样,我们可以删除下标k,因为它是时不变的。 通过将观察模型与状态相乘,我们得到:
We now have our state transformed into the format of measurement. So for this step, we calculate the residual ỹ(k) which is observed measurement minus calculated measurement.
现在,我们将状态转换为度量格式。 因此,对于这一步,我们计算观察到的测量值减去计算出的测量值后的残差ỹ(k) 。
2.2 Kalman gain:
2.2卡尔曼增益:
We have now arrived at the most cryptic equation of the Kalman filter algorithm, the computation of Kalman gain ( K(k) ). This is the real game player in the algorithm for which we went through all of this trouble. Kalman gain holds the information of uncertainties in state parameters fused with the uncertainties in observations of the instrument readings. P(k) holds uncertainty in state parameters while R(k) represents the observation noise matrix. These are fused into Kalman gain using the above equation. In the next steps, we will see the role of Kalman gain in enhancing our prior estimates.
现在,我们得出了卡尔曼滤波算法中最隐秘的方程式,即卡尔曼增益( K(k))的计算 。 这是我们遇到了所有麻烦的真正算法中的游戏者。 卡尔曼增益保持状态参数的不确定性信息与仪器读数观测值的不确定性相融合。 P(k)保持状态参数的不确定性,而R(k)代表观察噪声矩阵。 使用以上公式将它们融合到卡尔曼增益中。 在接下来的步骤中,我们将看到卡尔曼增益在增强我们先前的估计中的作用。
2.3 Update state:
2.3更新状态:
We now have X̂ (k|k-1), which is the estimate of the state which we calculated in the propagation step. We have ỹ(k), which is the residual we calculated in the innovation step, and we have K(k), Kalman gain which we calculated in the previous step. Based on these three we update the estimate of the state. The significance of k | k (read as k given k) in X̂ (k|k) is that we are enhancing our estimates which we calculated in the propagation step using the observed measurements.
现在我们有X̂(k | k-1),它是在传播步骤中计算出的状态的估计值。 我们有ỹ(k),这是我们在创新步骤中计算出的残差,而我们有K(k) ,即在上一步中计算出的卡尔曼增益。 基于这三个,我们更新状态的估计。 k的意义 X̂(k | k)中的 k (在给定k的情况下,读作k )是我们正在增强我们的估计值,该估计值是使用观察到的测量值在传播步骤中计算得出的。
To get an intuition of how this is happening, consider the state measured in the propagation step and the residual calculated in the measurement step. Both of the things kind of represent the same thing but in different formats. Where X̂ (k|k-1) represents the prior belief of state, the residual ỹ(k), represents the difference in measured state and prior belief. The Kalman gain acts as a bridge between them. It contains the information regarding the proportions in which the prior belief of state and the observations will be weighted to calculate the updated state. The cool thing about this is, you don’t need to worry about knowing which measurement contributes how much towards the estimate. All of that has been computed as part of the Kalman gain which contains all this information.
为了直观了解这种情况的发生,请考虑在传播步骤中测量的状态和在测量步骤中计算的残差。 两种事物都代表同一事物,但格式不同。 X̂(k | k-1)表示状态的先验信念,而残差ỹ(k)表示测量状态和先验信念的差。 卡尔曼增益充当它们之间的桥梁。 它包含有关比例的信息,状态的先验信念和观察将按权重进行加权以计算更新的状态。 与此有关的很酷的事情是,您不必担心知道哪种度量对估计有多大贡献。 所有这些都作为包含所有这些信息的卡尔曼增益的一部分进行了计算。
2.4 Update Estimate Covariance Matrix:
2.4更新估算协方差矩阵:
In this is the final step of the Kalman filter, we use the Kalman gain computed, the observation model, and the prior belief of estimate covariance to update the estimate covariance matrix. As Kalman gain holds the gain in information gathered from instruments, the uncertainties in state parameters decrease as we have gained information. With a continuous feed of the measurements, the Kalman filter is able to reduce the uncertainty in the car’s state and is able to localize the car.
在这是卡尔曼滤波器的最后一步,我们使用计算的卡尔曼增益,观测模型和估计协方差的先验信念来更新估计协方差矩阵。 由于卡尔曼增益保持了从仪器收集的信息的增益,因此,随着我们获得信息,状态参数的不确定性会降低。 通过连续提供测量值,卡尔曼滤波器能够减少汽车状态的不确定性,并能够对汽车进行定位。
摘要 (Summary)
We can summarize the algorithm as follows:
我们可以将算法总结如下:
Kalman filter algorithm 卡尔曼滤波算法UFF! That was a lot, wasn’t it! But by decoding the equations, line by line along with me, we have finally understood how Kalman filters work, and how it is implemented mathematically. Understanding the equations isn’t hard. Don’t let the notations and the linear algebra intrigue you. It’s more important to understand the meaning that they are trying to convey.
FF! 太多了,不是吗! 但是通过与我一起逐行解码方程,我们终于了解了卡尔曼滤波器的工作原理以及如何在数学上实现它。 了解方程式并不难。 不要让符号和线性代数引起您的兴趣。 理解他们试图传达的含义更为重要。
结论 (Conclusion)
Kudos! If you got everything, you now understand one of the most widely used algorithms for localization in the autonomous industry. There are variants to the original Kalman filter algorithms like Extended Kalman Filter (EKF) or Unscented Kalman Filter (UKF) to name a few but they all rely on the same concepts that we learned today. I would also suggest you go through Wikipedia, and read about Kalman filters there. If you found this very interesting, you can also checkout EKF and UKF online and try to see what limitations the original Kalman filter faces, and how they are tried to resolve in these variants.
荣誉! 如果您掌握了一切,现在您将了解自治行业中最广泛使用的本地化算法之一。 原始卡尔曼滤波器算法有多种变体,例如扩展卡尔曼滤波器(EKF)或无味卡尔曼滤波器(UKF)等,但它们都依赖于我们今天学习的相同概念。 我还建议您浏览Wikipedia,并在那里阅读有关Kalman过滤器的信息 。 如果您发现这很有趣,还可以在线签出EKF和UKF,并尝试查看原始Kalman滤波器面的局限性,以及如何解决这些变体。
翻译自: https://medium.com/team-rover/understanding-kalman-filter-and-its-equations-5fcc5d5fe61e
卡尔曼滤波滤波方程