第2章 单层感知器
神经网络是模拟人类神经系统的,深度学习是神经网络的又一个名词。首先我们先来了解什么是人工神经元。
1.1 人工神经元
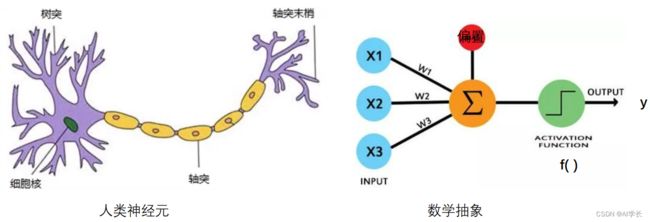
人工神经元是从人类神经元中抽象出来的数学模型。如下图:
该模型是1943年由心理学家Warren McCulloch和数学家Walter Pitts合作提出人工神经元,称为M-P模型。
其表达式如下:
计算过程的理解:
(1)求和:s = w1*x1+w2*x2+...+w3*x3;
(2) 如果 s > 阈值 输出1,否则输出0;
(3)变换 s-阈值>0,定义bias = -阈值,称为偏置。
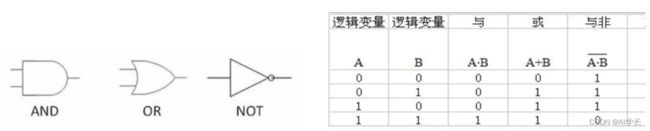
最初的研究是用来算法来理解逻辑运算:与门、或门、非门。
如下与或非运算真值表:
把其值表达在坐标上:
按照二分类的理解,圈是0类,三角形是1类。正好通过一条分割线分割:
其实M-P模型人为的设定好w和b参数,就可以解决简单的线性分类问题(与门、或门)。
局限性: 权值w和偏置b都是人为给定的,此模型没有"自我学习"能力。
下面我们来学习具有自我学习的模型 --- 单层感知器。
1.2 单层感知器
1.2.1 提出问题
M-P模型的参数w和b是通过手动设置的,显得有些不智能。
问题:如图,那么计算机能否自己计算找到合适的参数(w,b)?
或者说 如何找到一个合适的直线分割两类点(找到参数w,b)?
1.2.2 感知器模型
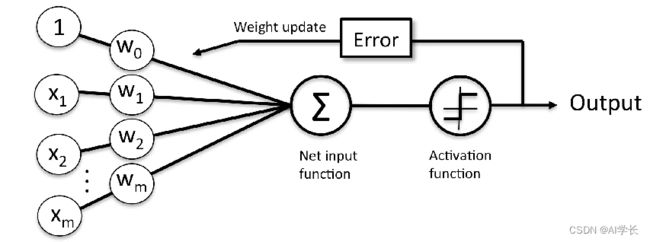
1958年美国心理学家Rosenblatt(弗兰克.罗森布拉)提出一种能够自我学习,具有单层计算单元的神经网络模型,叫感知器(perceptron)。 结构如下:
表达式:
其中,W是权重,b是偏置(上图w0);注意:W,X是向量形式。
激活函数f是一个阶跃函数(结果是简单的二分类0/1),其表达式:
1.2.3 感知器学习过程
感知器找到合适的w,b的过程如下:
(1)首先权重初始化,对权重w0(就是b),w1, w2 进行随机初始化;
(2)前向传播:输入样本对{X, Y},通过 Y=f(WX+b) 计算节点的实际输出(其中X={{x11,x12}, {x21,x22}, {x31,x32}...} 为输入信号矩阵,Y={y1,y2,y3...}为期望目标值 );
(3)计算误差:使用损失函数计算误差;
(4)反向传播:计算传递梯度,更新权重w和偏置b ;
按照 2-4步进行迭代,直到在训练集合达到期望的要求(例如:期望误差很小)。
1.2.4 损失函数
感知器学习的过程中,计算误差的函数称为损失函数。
损失函数模型训练中,表示随机事件的“风险”或“损失”的函数,即衡量误差大小的函数。
感知器使用均方误差MSE作为损失函数:
其中,n是个数,yi是当前值(真实),^yi是期望值(标签、预测); 1/2没有特殊意义,是为了求导后能约掉2系数。
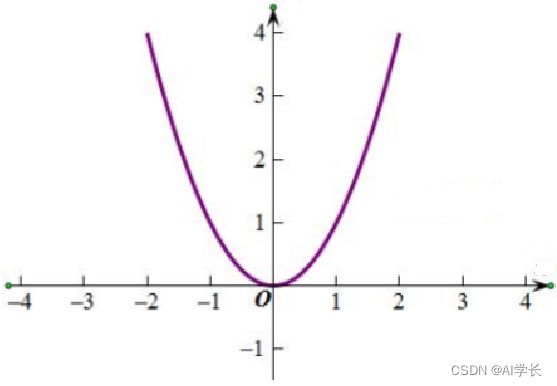
曲线图:
损失函数(二次方)曲线
在误差很小的时候,通常就是我们所期望的结果。
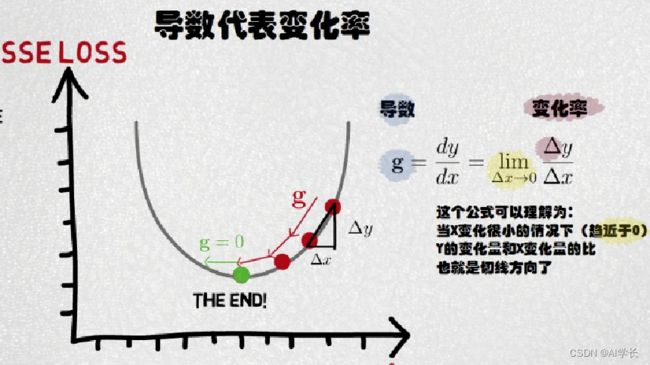
在二次方曲线中,导数等于0的地方就是误差最小的地方,那么问题是如何寻找这个地方?
感知器中,使用梯度下降法找到该处。
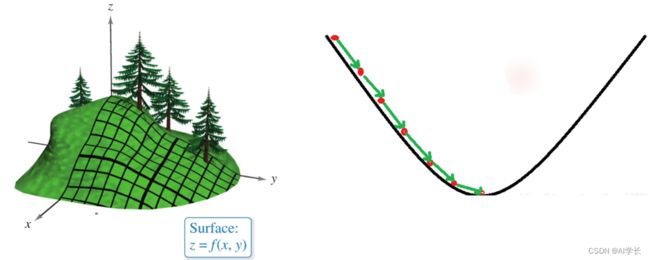
1.2.5 梯度下降法:理解
梯度下降法的基本思想可以类比为一个下山的过程。
假设场景:一个人被困在山上,需要从山上下来(找到山的最低点,山谷)。但此时山上的浓雾很大,导致可视度很低;因此,下山的路径就无法确定,必须利用自己周围的信息一步一步地找到最快下山的路。
利用梯度下降算法来帮助自己下山:首先以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着这个方向走一步(一段距离),然后又继续以当前位置为基准,再找最陡峭的地方,再走直到最后到达最低处。
1.2.6 梯度下降法:梯度
梯度:函数在该点的方向导数(偏导数)。
梯度一个向量,表示函数在该点处沿着该方向(梯度的方向)变化最快,变化率最大(梯度的模)。
如果损失函数代表着一座山,目标是找到这个函数的最小值(山底), 最快的下山的方式是沿着当前位置最陡峭的方向(梯度相反的方向)走,函数值下降最快,不断的反复直到走到函数的最小值。
1.2.7 权重更新
更新公式:新的参数 = 旧的参数 - 学习率*梯度
通过学习率(Learning rate)来定义每次参数更新的幅度,也叫学习步长。 学习率是一个超参数,可以预习设定,也可以通过超参数调优选择。
其中 是学习率,控制更新步长,训练人为设定0-1的值;负号表示梯度的反方向,变化率表示梯度的模。
1.3 感知器训练与门代码
与门真值表为训练集。
import numpy as np
def get_xy_data():
""" 与门的训练集 -- 真值表 """
x = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 0, 0, 1])
return x,y感知器与门模型:
import numpy as np
""" 定义感知器模型结构 """
class AndGateModel():
def __init__(self):
""" 初始化权重、偏置 """
self.w = np.random.normal(size=2) # 与门有2个权重
self.b = np.random.normal(size=1) # 1个偏置[0.5]
self.lr = 0.1 # 学习率(超参数)
def forward(self, x):
"""
前向计算
x -- [x1, x2]
1. y=wx + b
2. 激活函数计算
"""
y = x[0]*self.w[0] + x[1]*self.w[1] + self.b[0]
if y >= 0:
return 1
else:
return 0
def train(self, X, Y):
"""
X,Y -- 训练集
"""
for i in range(1000): # 迭代
j = 0
C = 0
for xi in X:
yi = self.forward(xi) # 前向计算
# 计算误差
Ci = np.power((Y[j] - yi), 2) / 2
C += Ci
# 更新权重跟偏置
if Ci > 0:
self.w[0] = self.w[0] + self.lr * (Y[j] - yi) * xi[0]
self.w[1] = self.w[1] + self.lr * (Y[j] - yi) * xi[1]
self.b[0] = self.b[0] + self.lr * (Y[j] - yi)
j += 1
print("epoch{} 误差:{} 权重:{} 偏置:{}".format(i, C, self.w, self.b))
# 什么时候退出?
if C <= 0:
print("=== 与门的4数据都正确了, 退出迭代")
break训练与门模型并保存参数:
if __name__ == "__main__":
# 训练
import data_manager
X, Y = data_manager.get_xy_data() # 读取数据集
model = AndGateModel() # 实例化类对象
model.train(X, Y) # 执行训练
# 验证训练结果是否正确
for xi in X:
print("验证 输入:{} 模型的前向计算结果:{}".format(xi, model.forward(xi)))
# 保存模型参数
np.savez("./params", model.w, model.b)读取模型参数并预测数据:
import numpy as np
if __name__ == "__main__":
# 加载参数
r = np.load("./params.npz")
print("权重", r["arr_0"])
print("偏置", r["arr_1"])
# 设置参数到网络结构
import model
and_model = model.AndGateModel()
and_model.w = r["arr_0"]
and_model.b = r["arr_1"]
# 预测
X = [[0,0], [0, 1], [1, 0], [1, 1]]
for xi in X:
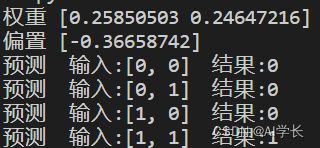
print("预测 输入:{} 结果:{}".format(xi, and_model.forward(xi)))结果如下:
python .\model.py
python .\predict_demo.py:
完整代码:https://download.csdn.net/download/qq_21386397/87567242
有帮助,一键三连哦~~~~~~~~~~~~~~~~~~~~~~~~~~~~