图论学习(一)
图的定义
一个图G定义为一个有序对(V,E),记为G=(V,E),其中
- V是一个非空集合,称为顶点集或点集,其元素称为顶点或点。
- E是由V中的点组成的无序点对构成的集合,称为边集,其元素称为边,且同一点对在E中可出现多次。
图G的顶点集记为V(G),边集记为E(G)。图G的顶点数(阶数)和边数可分别用符号n(G)和m(G)表示。
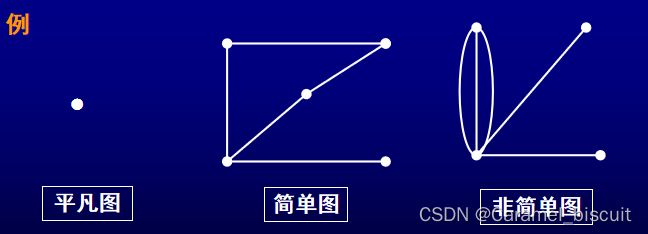
设V=v1, v2, v3, v4},E ={v1v2 , v1v2, v2v3 },则G=(V,E)是一个4阶图。
若用小圆点代表点,连线代表边,则可将一个图用“图形”来表示,如例中的图科表示为:
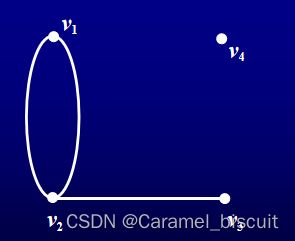
- 若边e=uv,此时称u和v是e的端点;并称u和v相邻,u(或v)与e相关联。若两条边有一个共同的端点,则称这两条边相邻。
- 孤立点:不与任何边相关联的点。
- 自环:两端点重合的边。
- 重边:连接两个相同顶点的边的条数,叫做边的重数,重数大于1的边称为重边。
- 点集与边集均为有限集合的图称为有限图。
- 只有一个顶点而无边的图称为平凡图。
- 边集为空的图称为空图。
- 既没有环也没有重边的图称为简单图,其它的图都称为复合图。
图的同构
定义:设有两个图G1=(V1,E1)和G2=(V2,E2),若在其顶点集合之间存在双射,即存在一一对应的关系:使得边之间有如下的关系:设u1, v1∈V1 , u2, v2∈V2, u1 ↔ u2, v1 ↔ v2, u1v1∈E1当且仅当u2v2∈E2,且u1v1的重数与u2v2相等,则称两图同构,记为G1≌G2。
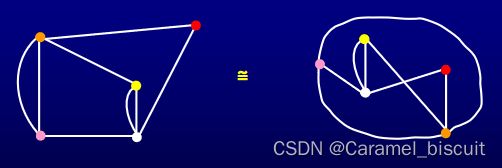
- 两个同构的图均有相同的结构,没有本质上的差异,差异只是顶点和边的名称不同。
- 图同构的几个必要条件:顶点数相同;边数相同;若将各点关联的边数记录下来,则所得到的数组相同。
- 在图的图形表示中我们可以不给图的点和边标上符号,这样的图称为非标定图,否则称为标定图。非标定图实际上是代表一类相互同构的图。

证明:作映射f:vi↔ui (i=1,2….,10),易知该映射为双射。
容易验证:


两图不同构。
若两图同构,则两图中唯一的与环相关联的两个点u与v一定相对于,而u的两个邻接点与v的两个邻接点状况不同。u邻接有一个关联着4条边的点,而v没有。
所以两图不同构。

分析:四个顶点的简单图最少边数为0,最多边数为6,所以可按边数进行枚举。
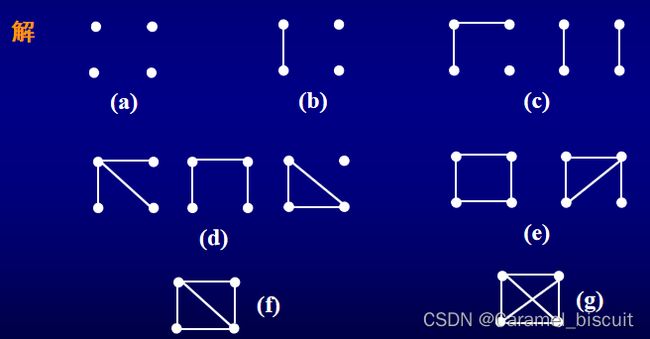
完全图,偶图,补图
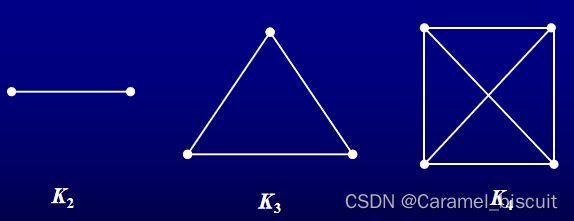
任意两点均相邻的简单图称为完全图。在同构意义下,n阶完全图只有一个,记为Kn。
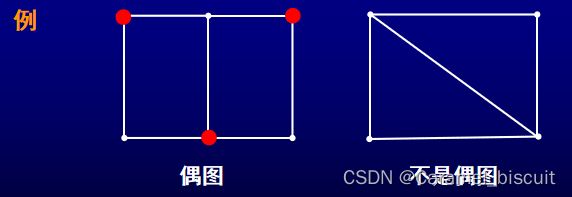
若一个图的点集可以分解为两个非空子集X和Y,使得每条边的一个端点在X中,另一个端点在Y中,则这样的图称为具有二分类(X,Y)的偶图或偶图。
**完全偶图是指具有二分类(X,Y)的简单偶图,其中X的每个顶点都与Y的每个顶点相连,若 |X|=m,|Y|=n,则这样的偶图记为Km,n。
**




度与度序列
设v为G的顶点,G中以v为端点的边的条数(环计算两次),称为点v的度数,简称为点v的度,记为dG (v),简记为d(v)。
- δ(G):图G的顶点的最小度
- Δ(G):图G的顶点的最大度
- 奇点:度数为奇数的顶点
- 偶点:度数为偶数的顶点
- k正则图:每个点的度均为k的简单图
完全图Kn和完全偶图Kn, n 均是正则图。
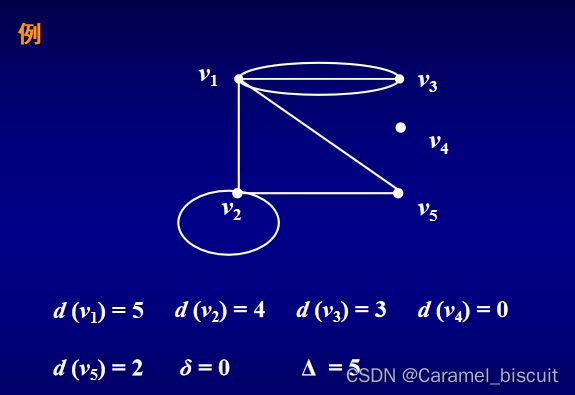
注:该图中各点度数之和等于14,恰好是边数7的两倍。

证明:因图G的任一一条边均有两个端点(可以相同),在计算时恰被计算两次(每个端点各被计算了一次),所以各点的度数之和恰好为边数的两倍。
![]()
设V1,V2分别是由G的奇点和偶点构成的集合,则由握手定理知:
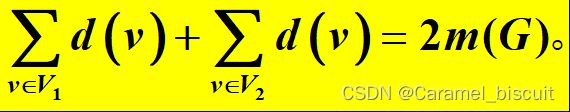
显然,第二个求和式为偶数,而第一个求和式中的每一项均为奇数,所以第一个求和式必然有偶数项,即度数为奇数的顶点个数必为偶数。

设G是n阶k正则图,因为度数之和nk为偶数,所以n和k不同时为奇数。


一个图G的各个点的度d1,d2,…,dn构成的非负整数组(d1,d2,…,dn)称为G的度序列。
定理:非负整数组(d1,d2,…,dn)是图的度序列的充要条件为:∑di 为偶数。
证明:必要性由握手定理立即得到。
如果所有度的和为偶数,则数组中奇数的个数必为偶数。
按照如下方式作图,若di为偶数,则在与之对应的点做di/2个环;对于剩下的偶数个奇数dj,两两配对,再在每个顶点作(dj-1)/2个环。
对于一个非负整数组(d1,d2,…,dn),若存在一个简单图以它为度序列,则称这个数组是可图的。可图的序列简称为可图序列或图序列。

证明:充分性显然,我们只需要证明必要性。
设G是Π对应的简单图,d(vi)=di。
- 情形1:点v1与点v2,v3,…,vd1+1邻接,则删去顶点v1及其关联的边所得到的图的度序列正好为Π1。
- 情形2:点v1与点vd1+2,…,vn 中的某些顶点邻接。不成立。
图的频序列
一个简单图G的n个点的度不能互不相同
因为图G是简单图,所以Δ(G)≤n−1。
- 情形1:若G没有孤立点,则

因为顶点个数是n,所以必有两个顶点读书相同。 - 情形2:若G中只有一个孤立点,设G1表示G去掉孤立点后的部分,则

同理,在G1中必有两顶点度数相同。 - 若G 有两个以上的孤立点,则定理显然成立。
设n阶图G的各点的度取s个不同的非负整数d1,d2,…,d3.又设di的点有bi个(∑bi=n),则称 (b1, b2,…, bs) 为G的频序列。
定理:一个n阶图G和它的补图有相同的频序列。
证明:由补图的定义知,点v在图G及其补图中的度数之和为n-1,即

因此,若G中有bi个度为di的点,则这bi个点在G的补图中的度变为n-1-di。
故G与其补图有相同的频序列。