【数据结构】线性表和顺序表

Yan-英杰的主页

悟已往之不谏 知来者之可追

---

目录

1.线性表

2.顺序表

        2.1 静态顺序表

        2.2 动态顺序表

        2.3移除元素

---

1.线性表

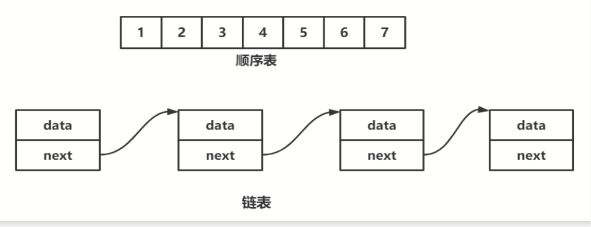
        线性表（linear list）是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表、链表、栈、队列、字符串...

        线性表在逻辑上是线性结构，也就说是连续的一条直线。但是在物理结构上并不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储。

2.顺序表

        2.1 静态顺序表

                 注:静态顺序表有个很大的缺点，空间分配多了浪费，分配少了不够用,我们通常使用动态顺序表

                typedef和define的区别？

                typedef通常用来定义类型名称，define通常用来定义常量

//define通常用来定义常量
#define N 10

//typedef通常用来定义类型名称
typedef int SLDataType;

//静态顺序表
//缺点:空间开少了不够用，开多了不够用
struct SeqList
{
	SLDataType a[N];
	SLDataType size;
};

       2.2 动态顺序表

                优点:当内存堆内存不够用时,我们可以进行申请

                函数定义

#pragma once
#include
#include
#include
#define INIT_CAPACITY 4
typedef int SLDataType;
typedef struct SeqList
{
	int capacity;
	int size;
	SLDataType* a;

}SL;

//初始化结构体
void SLInit(SL* ps);

//销毁结构体
void DestorySL(SL* ps);

//扩容
void CheckCapacity(SL* ps);

//头插
void SLPushFront(SL* ps, SLDataType x);
//头删
void SLPopFront(SL* ps);
//尾插
void SLPushBack(SL* ps,SLDataType x);
//尾删
void SLPopBack(SL* ps);
//打印
void SLPrint(SL* ps);
//查找
void FindSL(SL* ps);

        函数实现

#define _CRT_SECURE_NO_WARNINGS 1
#include "SeqList.h"

void SLInit(SL* ps)
{
	ps->a = (SLDataType*)malloc(sizeof(SLDataType)* INIT_CAPACITY);
	if (ps->a == NULL)
	{
		perror("fail malloc:");
		return;
	}
	ps->size = 0;
	ps->capacity = INIT_CAPACITY;
}

void DestorySL(SL* ps)
{
	free(ps->a);
	ps->a = NULL;
	ps->capacity = 0;
	ps->size = 0;
}

//扩容
void CheckCapacity(SL* ps)
{
	SLDataType* tmp = (SLDataType*)realloc(ps->a,sizeof(INIT_CAPACITY)*ps->capacity*2);
	if (tmp == NULL)
	{
		perror("fail:realloc");
		return;
	}
	ps->a = tmp;
	ps->capacity *= 2;
}

//头插
void SLPushFront(SL* ps,SLDataType x)
{
	assert(ps);
	CheckCapacity(ps);
	int i = 0;
	for (i=ps->size; i>=0; i--)
	{
		ps->a[i] = ps->a[i - 1];
	}
	ps->a[0] = x;
	ps->size++;
}

//头删
void SLPopFront(SL * ps)
{
	assert(ps);
	int i = 0;
	for (i=0; isize; i++)
	{
		ps->a[i] = ps->a[i + 1];
	}
	ps->size--;
}

//尾插
void SLPushBack(SL* ps,SLDataType x)
{
	//断言
	assert(ps);
	CheckCapacity(ps);
	ps->a[ps->size] = x;
	ps->size++;
}

//尾删
void SLPopBack(SL* ps) 
{
	assert(ps);
	ps->size--;
}

//打印
void SLPrint(SL* ps)
{
	assert(ps);
	int i = 0;
	for (i=0; isize; i++)
	{
		printf("%d ",ps->a[i]);
	}
}

//查找指定位置的数字
void FindSL(SL* ps,int x)
{
	assert(ps);
	int i = 0;
	printf("%d", ps->a[x - 1]);
}

        函数调用

#define _CRT_SECURE_NO_WARNINGS 1
#include "SeqList.h"
void SeqListTest()
{
	SL s;
	SLInit(&s);
	SLPushBack(&s, 1);
	SLPushBack(&s, 2);
	SLPushBack(&s, 3);
	SLPushBack(&s, 4);
	SLPushBack(&s, 4);
	SLPushFront(&s, 4);
	SLPushFront(&s, 4);
	SLPrint(&s);
	FindSL(&s, 4);
}

int main()
{
	SeqListTest();
	return 0;
}

        2.3移除元素

        给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。

        不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

        元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

说明:

        为什么返回数值是整数，但输出的答案是数组呢?

        请注意，输入数组是以「引用」方式传递的，这意味着在函数里修改输入数组对于调用者是可见的。

        你可以想象内部操作如下:

// nums 是以“引用”方式传递的。也就是说，不对实参作任何拷贝
int len = removeElement(nums, val);

// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
    print(nums[i]);
}

示例 1：

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例 2：

输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

提示：

    0 <= nums.length <= 100
    0 <= nums[i] <= 50
    0 <= val <= 100

解析：

int removeElement(int* nums, int numsSize, int val){
int src = 0, dst = 0;
	while (src < numsSize)
	{
		if (nums[src] != val)
		{
			nums[dst++] = nums[src++];
		}
		else 
		{
			src++;
		}
	}
    return dst;
}