Introduction to modern cryptography 第一章阅读笔记

---

前言

本系列读书笔记是基于个人对于《Introduction to modern cryptography》的阅读写下的，将会不定期更新其他章节的阅读笔记，本章为开篇第一章。文章中图片均来源于《Introduction to modern cryptography》一书。

---

1.1 密码学以及现代密码学

  密码学，在字典中的含义是“编码或解码的艺术”，主要针对的是编码。时至今日，其内涵已经扩展到包括完整性保障、密钥交换、验证协议、电子投票以及加密货币等各个方面。而对应的，现代密码学涵盖保护数字信息、数字系统和分布式计算免遭攻击的数学技术研究。
  从时间上看，二者大致上以1980s为分界线，在此之前的称为古典密码，之后的成为现代密码。
  总的来说，密码学已经从之前的一种用以保护少数特定应用场景的信息机密性的启发式的技巧发展成为一门帮助全世界普通人保障系统广泛化的科学。

1.2 私钥密码的设定

(1) 一些定义

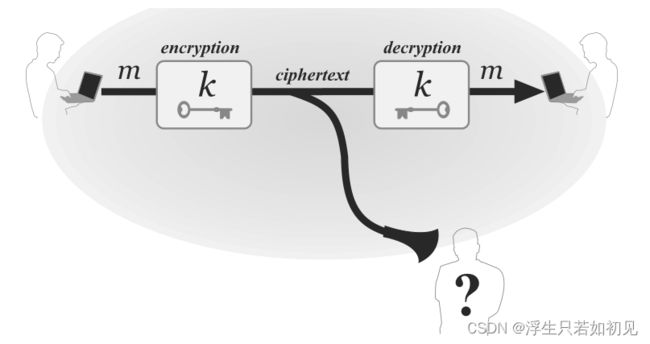
  对称加密：在对称加密的场景下，通信双方共享密钥，发送方可使用之加密明文并将其以密文形式发送至接收方，接收方使用相同的密钥解密密文并恢复明文。
  对称密码有两个典型的应用方向：空间上，同一时间内两不同地点的通信双方可使用对称密码满足保密通信的要求；时间上，同一地点的不同时间维度的双方亦可使用对称密码满足保密通信的要求。

(2) 密码方案的语法

• Gen: 密钥生成算法(概率算法)，可从特定分布中输出密钥。
• Enc: 加密算法，输入密钥 k 和明文 m，输出密文 c，可记作 $En{c}_k(m)$.
• Dec: 解密算法，输入密钥 k 和密文 c，输出明文 m，可记作 $De{c}_k(c)$.

  以上算法需满足以下公式：
$$De{c}_k(En{c}_k(m))=m$$

(3) Kerckhoffs原理

  密码方案并不需要保密，而且它必须很容易被敌方获取。换一种说法，密码方案的安全性不依赖于密码方案的保密，而是只依赖于密钥的隐秘性。
  该原理有三种主要依据：

• 保证密钥的隐秘性比保证整个密码方案的安全性容易很多。
• 再次通信时，更换密钥比更换整个密码方案更容易。
• 在广泛使用前，向公众公布密码方案可检查出可能存在的弱点，使 1) 不同用户兼容， 2）公众可使用经过大量审查后的强方案。

1.3 一些密码方案

(1) Caesar’s cipher

  凯撒密码是目前最古老的密码之一，其核心点在于明文通过右移三位进行加密。

(2) shift cipher

$$\begin{gathered} Gen()\to k \\ En{c}_k(m_1\cdot \cdot \cdot m_l)=c_1\cdot \cdot \cdot c_l,c_i=[(m_i+k)mod26] \\ De{c}_k(c_1\cdot \cdot \cdot c_l)=m_1\cdot \cdot \cdot m_l,m_i=[(c_i-k)mod26] \end{gathered}$$

(3) 充足密钥空间原则

  移位密码可以被穷举破解，原因在于移位密码的密钥只存在26种可能，只需尝试每种可能再取其中最合理的结果便可完成破解，故可引出以下原则：
$$\begin{gathered} 任何安全加密方案都需要一个足够大的密钥空间 \\ 以保证穷举攻击是难以做到的 \end{gathered}$$

(4) mono-alphabetic substitution cipher

  在该密码方案中，密文和明文的映射关系是随机的，但是需要保证此映射关系是一对一的，并由此使得密钥空间包含字母表中所有的双射。
  该方案保证了密钥空间的规模足够大，但是仍然会被攻击者利用英语的统计特性加以攻击：

• 对于任意密钥，字母间的映射关系是固定的
• 英语中所有字母的概率分布是已知的，大体量文本中字母的频率可侧面印证

(5) 移位密码的改良攻击

  在之前的移位密码的攻击中，我们需要尝试每种密钥可能并选出结果最合理的解，该方法的缺点在于电脑很难选择出人类认知中的合理。更重要的是，当明文本身并不是语言意义上合理时，保证解密出来的明文合理已经毫无作用。而在下列方法中，明文只需要满足和英语具有相同分布即可：
  用 0-25 分别表示英文字母 a-z，$p_i$表示第 i 个字母出现的频率，则可得到以下结论：
$$\sum _{i=0}^{25}{p}_i^2\approx 0.065$$
  在得到一些密文的情况下，令$q_i$表示密文中第 i 个字母出现的频率，并假设密钥为 k，则可认为$p_i$和$q_{i+k}$对应，于是我们计算每个可能的密钥取值$j\in \{0,...,25\}$，当得到的$I_j$和$I_k\approx 0.065$最接近时便可认为$j=k$
$$I_j\stackrel{def}{=}\sum _{i=0}^{25}{p}_i\cdot q_{i+j}$$

(6) Vigenere cipher

  维吉尼亚密码是多表移位密码的典型，可被认为是在不同明文区域中使用不同移位密码实例。密钥可被视为一串字母，加密是通过按密钥的扩展字符所表示的数量移动每个明文文本字符，当密钥长度为 1 时退化为移位密码。示例如下：

(7) 维吉尼亚密码的攻击

  当密钥长度(t)已知的情况下，攻击该密码方案是非常容易的：我们可以将密文分为 t 个部分(按以下方式进行组合)，其中每个部分都可以使用移位密码的方式进行破解，可暴力破解亦可利用统计规律破解。
$$c_j,c_{j+t},c_{j+2t},j\in \{1,...,t\}$$
  当 t 未知时，破解该密码方案的难度并未过度提升，原因如下：

• 只要密钥的最大长度 T 不是非常大，我们便可以重复上述攻击 T 次，而且其中正确结果将会更加好辨认
• Kasiski’s method：由于英语固有的语法结构，导致一些特定的双字母组和三字母组经常出现，于是我们便可以找密文中重复出现的三字母组，其间距极有可能是密钥长度 t 的倍数

  以上对维吉尼亚密码的攻击需要攻击者能够得到远大于密钥长度的密文，以确保计算得到的频率接近英语中字母的频率分布。

1.4 现代密码学的原则

1.4.1 形式化定义

• 形式上的定义通过给出清晰的描述让人们理解包括哪些威胁以及需要哪些安全保证
• 定义提供了评估和分析结构的方式
• 定义能够实现不同方案间的对比，对密码方案可模块化转移

安全加密定义

  总的来说，安全性定义由两部分组成：安全保证和威胁模型，安全保证定义方案要阻止攻击者的行为，威胁模型阐述攻击者的能力、攻击者能够执行的行为。

安全保证

• 攻击者不能恢复密钥
• 攻击者不能从密文中恢复明文
• 攻击者不能从密文中恢复明文的任意字母
• 无论攻击者有任何信息，密文都不能泄露任何有关明文的额外信息

威胁模型

• 仅密文攻击：攻击者只能获取密文
• 已知明文攻击：攻击者获得部分明文/密文对
• 选择明文攻击：攻击者可以选择明文进行加密得到密文
• 选择密文攻击：攻击者可以选择密文进行解密得到明文

1.4.2 精确假设

• 假设的有效性：假设被检查和测试的次数越多，越能说明假设为真。
• 假设间的比较：人们偏向于选择更弱和研究次数更多的假设
• 理解必要假设：加密方案经常基于潜在的逻辑块，若在后续发现了该逻辑块的弱点，只需检查所需假设是否被新弱点影响来确保密码方案的安全性

  证明密码方案的安全性基于某些其他假设而不直接假设密码方案是安全的原因如下：

• 一个被研究多年的假设优先于一个伴随新结构提出的假设
• 密码设计时偏好更简单的假设
• 低层次的假设可被移植于其他结构
• 低层次假设满足模块化

1.4.3 安全性证明

  在密码学中，严格证明一个结构满足特定假设下的给定定义是十分重要的。相对于定义和假设，安全性证明提供了一个更加坚实的保证:没有攻击者能攻击成功;这比用无原则的或启发式的方法来解决问题要好得多。
  如果不能证明任何拥有特定资源的对手都不能破坏某个方案，我们只能凭直觉认为情况就是如此。经验表明，在密码学和计算机安全方面的直觉是灾难性的。