蓝桥杯刷题总结---第六周

一.旅行家的预算

一个旅行家想驾驶汽车以最少的费用从一个城市  到另一个城市（假设出发时油箱是空的）。给定两个城市之间的距离D1、汽车油箱的容量C（以升为单位）、每升汽油能行驶的距离D2、出发点每升汽油价格P  和沿途油站数N（N可以为零），油站i离出发点的距离Di、每升汽油价格Pi（i=1，2，……N）。计算结果四舍五入至小数点后两位。如果无法到达目的  地，则输出“No  Solution”。

思路:使用贪婪策略,对每一个结点分析,若存在比当前结点小且可以到达的结点则停车补油,若不存在则在可到达范围内选择一个油价最小的站点补油,并且需要将原来的油用完.

D1,C,D2,P,N=map(eval,input().strip().split())
station=[list(map(eval,input().strip().split()))for i in range(N)]
fmax=0
fmin=0
ans=0
now=0
now_station=-1
max_dis=C*D2
while len(station):

    flag=True
    fmax=fmin
    while fmin=station[fmax][0]:
        flag=False
        if now_station==-1 and station[fmax][1]<=P:
            fmin=fmax
            break
        if now_station>=0 and station[fmax][1]<=station[now_station][1]:
            fmin=fmax
            break
        if station[fmin][1]>=station[fmax][1]:
            fmin=fmax
        fmax+=1
    if flag:
        if now_station==len(station)-1 and now+max_dis>=D1:
            ans+=station[now_station][1]*(D1-now)
            print("{:.2f}".format(ans / D2))
            break
        print("No Solution")
        break
    if now_station<0:
        if P=D1:
                ans+=P*D1
                print("{:.2f}".format(ans / D2))
                break
            now+=max_dis
            ans+=max_dis*P
        else:
            now+=station[fmin][0]
            ans+=now*P
        now_station=fmin
    else:
        if station[now_station][1]=D1:
        print("{:.2f}".format(D1*P/D2))
    else:
        print("No Solution")

二.星际交流

人类终于登上了火星的土地并且见到了神秘的火  星人。人类和火星人都无法理解对方的语言，但是我们的科学家发明了一种用数字交流的方法。这种交流方法是这样  的，首先，火星人把一个非常大的数字告诉人类科学家，科学家破解这个数字的含义后，再把一个很小的数字加到这个大数上面，把结果告诉火星人，作为人类的回  答。
火星人用一种非常简单的方式来表示数字——掰手指。火星人只有一只手，但这只手上有成千上万的手指，这些手指排成一列，分别编号为1，2，3……。火星人的任意两根手指都能随意交换位置，他们就是通过这方法计数的。
一个火星人用一个人类的手演示了如何用手指计数。如果把五根手指——拇指、食指、中指、无名指和小指分别编号为1，2，3，4和5，当它们按正常顺序  排列  时，形成了5位数12345，当你交换无名指和小指的位置时，会形成5位数12354，当你把五个手指的顺序完全颠倒时，会形成54321，在所有能够形  成的120个5位数中，12345最小，它表示1；12354第二小，它表示2；54321最大，它表示120。下表展示了只有3根手指时能够形成的6个  3位数和它们代表的数字：
三进制数
123
132
213
231
312
321
代表的数字
1
2
3
4
5
6
现在你有幸成为了第一个和火星人交流的地球人。一个火星人会让你看他的手指，科学家会告诉你要加上去的很小的数。你的任务是，把火星人用手指表示的数  与科  学家告诉你的数相加，并根据相加的结果改变火星人手指的排列顺序。输入数据保证这个结果不会超出火星人手指能表示的范围。

思路:使用全排列,但是C语言的next_permutation和python里的itertools里面的permutation的排列结果不相同,需要用python重新构造一个排列函数

def next_permutation(a):
    """Generate the lexicographically next permutation inplace.

    https://en.wikipedia.org/wiki/Permutation#Generation_in_lexicographic_order
    Return false if there is no next permutation.
    """
    # Find the largest index i such that a[i] < a[i + 1]. If no such
    # index exists, the permutation is the last permutation
    for i in reversed(range(len(a) - 1)):
        if a[i] < a[i + 1]:
            break  # found
    else:  # no break: not found
        return False  # no next permutation

    # Find the largest index j greater than i such that a[i] < a[j]
    j = next(j for j in reversed(range(i + 1, len(a))) if a[i] < a[j])

    # Swap the value of a[i] with that of a[j]
    a[i], a[j] = a[j], a[i]

    # Reverse sequence from a[i + 1] up to and including the final element a[n]
    a[i + 1:] = reversed(a[i + 1:])
    return True
N=int(input().strip())
M=int(input().strip())
nums=list(map(int,input().strip().split()))
for _ in range(M):
    next_permutation(nums)
for i in nums:
    print(i,end=' ')

三.连续正整数和

78这个数可以表示为连续正整数的和，1+2+3，18+19+20+21，25+26+27。

思路:使用高斯求和

num=int(input())
for n in range(1,num//2+1):
    for m in range(n+1,num//2+2):
        if (n+m)*(m-n+1)==2*num:
            print(n,m)
        elif (n+m)*(m-n+1)>2*num:
            break

四.log大侠

 atm参加了速算训练班，经过刻苦修炼，对以2为底的对数算得飞快，人称Log大侠。
  一天，Log大侠的好友 drd 有一些整数序列需要变换，Log大侠正好施展法力...
变换的规则是： 对其某个子序列的每个整数变为: [log_2 (x) + 1]  其中 [] 表示向下取整，就是对每个数字求以2为底的对数，然后取下整。
例如对序列 3 4 2 操作一次后，这个序列会变成 2 3 2。
 drd需要知道，每次这样操作后，序列的和是多少。

from math import *
n,m=map(int,input().split())
def log_2(num):
    return int(log(num,2)+1)
nums=list(map(int,input().split()))
area=[list(map(int,input().split())) for i in range(m)]
for L,R in area:
    for i in range(L-1,R):
        nums[i]=log_2(nums[i])
    print(sum(nums))

五.排列序数

 如果用a b c d这4个字母组成一个串，有4!=24种，如果把它们排个序，每个串都对应一个序号：
  abcd  0
  abdc  1
  acbd  2
  acdb  3
  adbc  4
  adcb  5
  bacd  6
  badc  7
  bcad  8
  bcda  9
  bdac  10
  bdca  11
  cabd  12
  cadb  13
  cbad  14
  cbda  15
  cdab  16
  cdba  17
  ...
 现在有不多于10个两两不同的小写字母，给出它们组成的串，你能求出该串在所有排列中的序号吗？

思路:使用全排列函数,但是这里可以使用python自带的全排列函数,自己构建则会超时

import itertools
n = input()
x = sorted(n)
ans=0
for i in itertools.permutations(x):
    if i==tuple(n):
        print(ans)
        break
ans+=1

六.重复模式

作为 drd 的好朋友，技术男 atm 在 drd 生日时送给他一个超长字符串 S 。atm 要 drd 在其中找出一个最长的字符串 T ，使得 T 在 S 中至少出现了两次，而他想说的秘密就藏在 T 中。 

 由于字符串实在是太长了，drd 总是找不到合适的 T 。于是 drd 请你帮他找到这个 T 的长度。

思路:贪婪策略,从最大的长度开始判断,创建字典保存每一个长度被遍历过的字符串,如果字典不为0,则说明之前出现过

from collections import defaultdict
s=input()
n=len(s)-1
flag=True
while n>0 and flag:
    d=defaultdict(int)
    for i in range(len(s)-n+1):
        if d[s[i:i+n]]==0:
            d[s[i:i+n]]=1
        else:
            print(n)
            flag=False
            break
    n-=1

七.秘文搜索

福尔摩斯从X星收到一份资料，全部是小写字母组成。
他的助手提供了另一份资料：许多长度为8的密码列表。
福尔摩斯发现，这些密码是被打乱后隐藏在先前那份资料中的。
请你编写一个程序，从第一份资料中搜索可能隐藏密码的位置。要考虑密码的所有排列可能性。

思路:不用直接全排列,我们使用字典保存密文中所有字母出现的次数,再遍历资料中所有长度为8的子串即可.

from collections import defaultdict
text=input().strip()
n=int(input().strip())
ans=0
mima=[input().strip() for i in range(n)]
def num_in (ss):
    d=defaultdict(int)
    for i in ss:
        d[i]+=1
    return d
text_key=[num_in(text[i:i+8]) for i in range(len(text)-7)]
for i in text_key:
    for j in mima:
        temp_d=num_in(j)
        flag=True
        for jj in j:
            if temp_d[jj]!=i[jj]:
                flag=False
                break
        if flag:
            ans+=1
print(ans)

八.邮票

给定一个信封，有N（1≤N≤100）个位置可以贴邮票，每个位置只能贴一张邮票。我们现在有M(M< =100)种不同邮资的邮票，面值为X1,X2….Xm分（Xi是整数，1≤Xi≤255），每种都有N张。
显然，信封上能贴的邮资最小值是min(X1,  X2,  …,  Xm)，最大值是  N*max(X1,  X2,  …,　　Xm)。由所有贴法得到的邮资值可形成一个集合（集合中没有重复数值），要求求出这个集合中是否存在从1到某个值的连续邮资序列，输出这个序列的  最大值。
例如，N=4，M=2，面值分别为4分，1分，于是形成1，2，3，4，5，6，7，8，9，10，12，13，16的序列，而从1开始的连续邮资序列为1，2，3，4，5，6，7，8，9，10，所以连续邮资序列的最大值为10分。

思路:使用dfs记忆递归加剪枝回溯,flags[num][0]记录总面值为num是否被访问过,flags[num][1]记录总面值为n需要的牌数,将牌从大到小排序,如果有总牌数已经被达到并且数量比目前的n少,则剪枝

N=int(input().strip())
M=int(input().strip())
stamp=list(map(int,input().strip().split()))
stamp.sort(reverse=True)
def dfs(num_sum,n):
    global N,M,stamp,flags
    if n>N:
        return
    if flags[num_sum][0]==1 and flags[num_sum][1]<=n:
        return
    else:
       # print(num_sum)
        flags[num_sum][0]=1
        flags[num_sum][1]=n
        for i in stamp:
            dfs(num_sum+i,n+1)
if stamp[len(stamp)-1]>1:
    print(0)
else:
    flags=[[0,-1] for i in range(N*stamp[0]+1)]
    dfs(0,0)
    for i in range(len(flags)):
        if flags[i][0]==0:
            print(i-1)
            break

九.邮票面值设计(dfs回溯加动态规划)

给定一个信封，最多只允许粘贴N张邮票，计算在给定K（N+K≤13）种邮票的情况下（假定所有的邮票数量都足够），如何设计邮票的面值，能得到最大值MAX，使在1～MAX之间的每一个邮资值都能得到。
例如，N=3，K=2，如果面值分别为1分、4分，则在1分～6分之间的每一个邮资值都能得到（当然还有8分、9分和12分）；如果面值分别为1分、  3分，则在1分～7分之间的每一个邮资值都能得到。可以验证当N=3，K=2时，7分就是可以得到的连续的邮资最大值，所以MAX=7，面值分别为1分、  3分。

思路:动态规划加dfs,dp[i]记录总牌数达到i所需的最小牌的数目,如果dp[i]数目大于N则最大的总牌数为i-1,如上题利用dfs记录寻找最大的牌数及其组合

N,M=map(int,input().strip().split())
arr=[]
ans=[0 for i in range(M)]
max_ans=-1
def init_dp():
    global arr,N,M
    dp=[float('inf') for i in range(500)]
    dp[0]=0
    for j in range(len(dp)):
        for i in range(len(arr)):
            if j-arr[i]>=0:
                dp[j]=min(dp[j],dp[j-arr[i]]+1)
        if dp[j]>N:
            return j-1
def dfs(max_num,count):
    global N,M,arr,ans,max_ans
    if count==M:
        if max_num>max_ans:
            for i in range(len(arr)):
                ans[i]=arr[i]
            max_ans=max_num
        return
    for i in range(max_num+1,arr[len(arr)-1],-1):
        arr.append(i)
        dfs(init_dp(),count+1)
        arr.pop()
arr.append(1)
dfs(N,1)
for i in ans:
    print(i,end=' ')
print()
print("MAX={}".format(max_ans))

十.字符串编辑

从键盘输入一个字符串，并以字符’.’结束。编辑功能有：
1  D：删除一个字符，命令的方式为：D  a  其中a为被删除的字符，例如：D  s  表示删除字符’s’，若字符串中有多个  ‘s’,则删除第一次出现的。
2  I：插入一个字符，命令的格式为：I  a1  a2  其中a1表示插入到指定字符前面，a2表示将要插入的字符。例如：I  s  d  表示在指定字符  ’s’  的前面插入字符  ‘d’  ，若原串中有多个 ‘s’，则插入在最后一个字符的前面。
3  R：替换一个字符，命令格式为：R  a1  a2  其中a1为被替换的字符，a2为替换的字符，若在原串中有多个a1则应全部替换。
在编辑过程中，若出现被改的字符不存在时，则给出提示信息。

思路:很简单的一个模拟

s=input().strip()
order=list(input().strip().split())
flag=True
if order[0]=='D':
    for i in range(len(s)):
        if s[i]==order[1]:
            s=s[:i]+s[i+1:]
            print(s)
            flag=False
            break
elif order[0]=='R':
    for i in range(len(s)):
        if s[i]==order[1]:
            flag=False
            s=s[:i]+order[2]+s[i+1:]

    if not flag:
        print(s)
else:
    for i in range(len(s)-1,-1,-1):
        if s[i]==order[1]:
            flag=False
            s=s[:i]+order[2]+s[i:]
            print(s)
            break
if flag:
    print("no exist")

十一.删除多余括号

从键盘输入一个含有括号的四则运算表达式，要求去掉可能含有的多余的括号，结果要保持原表达式中变量和运算符的相对位置不变，且与原表达式等价,不要求化简。另外不考虑'+''-'用作正负号的情况，即输入表达式不会出现(+a)或(-a)的情形。

思路:利用正则表达式将表达式的所有括号作为分隔符将单词分隔开,再记录每个单词中最小优先级的符号和单词开头和结尾的符号(这会影响旁边的括号),如果单词中最小的符号优先级大于旁边的优先级,则括号可以去除,(a*b)/c和(a+b)-c除外.

import re
d=dict()
d['+']=1
d['-']=2
d['*']=3
d['/']=4
def words_work(words):
    ans=''
    level=[0 for i in range(len(words)+2)]
    per_level=[0 for i in range(len(words)+2)]
    for i in range(len(words)):
        fmin=5
        for j in words[i]:
            if j in ['+','-','*','/']:
                if d[j]=per_level[i] and level[i+1]>=per_level[i+2]) or len(words[i])==1 or(level[i+1]>=per_level[i] and level[i+1]==1 and per_level[i+2]==2) or(level[i+1]>=per_level[i] and level[i+1]==3 and per_level[i+2]==4):
            ans+=words[i]
        else:
            ans+='('+words[i]+')'
    print(ans)
while True:
    try:
        in_put = re.split('[()]', input().strip())
        words = []
        for i in in_put:
            if i:
                words.append(i)
        words_work(words)
    except:
        break

十二.稍大的串

串可以按照字典序进行比较。例如：
  abcd 小于 abdc
  如果给定一个串，打乱组成它的字母，重新排列，可以得到许多不同的串，在这些不同的串中，有一个串刚好给定的串稍微大一些。科学地说：它是大于已知串的所有串中最小的串。你的任务就是求出这个“稍大的串”。

思路:利用python实现c++stl库中的next_permutation方法

def next_permutation(a):
    """Generate the lexicographically next permutation inplace.

    https://en.wikipedia.org/wiki/Permutation#Generation_in_lexicographic_order
    Return false if there is no next permutation.
    """
    # Find the largest index i such that a[i] < a[i + 1]. If no such
    # index exists, the permutation is the last permutation
    for i in reversed(range(len(a) - 1)):
        if a[i] < a[i + 1]:
            break  # found
    else:  # no break: not found
        return False  # no next permutation

    # Find the largest index j greater than i such that a[i] < a[j]
    j = next(j for j in reversed(range(i + 1, len(a))) if a[i] < a[j])

    # Swap the value of a[i] with that of a[j]
    a[i], a[j] = a[j], a[i]

    # Reverse sequence from a[i + 1] up to and including the final element a[n]
    a[i + 1:] = reversed(a[i + 1:])
    return True
n=input()
nn=[i for i in n]
next_permutation(nn)
print(''.join(nn))

十三.生物芯片

X博士正在研究一种生物芯片，其逻辑密集度、容量都远远高于普通的半导体芯片。
博士在芯片中设计了 n 个微型光源，每个光源操作一次就会改变其状态，即：点亮转为关闭，或关闭转为点亮。
这些光源的编号从 1 到 n，开始的时候所有光源都是关闭的。
博士计划在芯片上执行如下动作：
所有编号为2的倍数的光源操作一次，也就是把 2 4 6 8 ... 等序号光源打开
  所有编号为3的倍数的光源操作一次, 也就是对 3 6 9 ... 等序号光源操作，注意此时6号光源又关闭了。
所有编号为4的倍数的光源操作一次。
.....
直到编号为 n 的倍数的光源操作一次。

X博士想知道：经过这些操作后，某个区间中的哪些光源是点亮的。

思路:这是在计算因数的个数的奇偶,判断是否是平方数就可以

N,L,R=map(int,input().strip().split())
def yinshu(n):
    return (n**0.5-int(n**0.5))==0
lights=[yinshu(i) for i in range(L,R+1)]
print(lights.count(False))

十四.切开字符串

Pear有一个字符串，不过他希望把它切成两段。
这是一个长度为N（<=10^5）的字符串。
Pear希望选择一个位置，把字符串不重复不遗漏地切成两段，长度分别是t和N-t（这两段都必须非空）。
Pear用如下方式评估切割的方案：
定义“正回文子串”为：长度为奇数的回文子串。
设切成的两段字符串中，前一段中有A个不相同的正回文子串，后一段中有B个不相同的非正回文子串，则该方案的得分为A*B。
注意，后一段中的B表示的是：“...非正回文...”，而不是: “...正回文...”。
那么所有的切割方案中，A*B的最大值是多少呢？

思路:分别正序和倒序遍历字符串,找到以i为结尾的正回文子串或者非正回文子串,再求前缀和,查找最大项

n=int(input())
string=input().strip()
is_same=set()
not_same=set()
def is_son(s):
    global is_same
    if len(s)%2==0:
        return False
    if s in is_same:
        return False
    return s==s[::-1]
sum_son=[0 for i in range(n)]
sum_not_son=[0 for i in range(n)]
for i in range(len(string)-1):
    for j in range(i,len(string)):
        if is_son(string[i:j+1]):
            sum_son[j]+=1
            is_same.add(string[i:j+1])
ss=string[::-1]
for i in range(len(string)-1):
    for j in range(i,len(string)):
        if not is_son(ss[i:j+1]) and ss[i:j+1] not in  is_same and  ss[i:j+1] not in not_same:
            sum_not_son[j]+=1
            not_same.add(ss[i:j+1])
for j in range(1,n):
    sum_son[j]+=sum_son[j-1]
    sum_not_son[j]+=sum_not_son[j-1]
ans=0
sum_not_son.reverse()
for i in range(2,n-2):
    ans=max(ans,sum_son[i]*sum_not_son[i+1])
print(ans)

十五.输出米字型

根据输入的正整数n 

米字形由一个(2n-1)*(2n-1)的矩阵组成，矩阵包含从大写A开始的n个字母

例如:n=3时，包含A,B,C；n=4时，包含A,B,C,D。
矩阵的正中间为n个字母中字典序最大的那个，从这个字母开始，沿着西北、正北、东北、正西、正东、西南、正南、东南八个方向各有一条由大写字母组成的直线。并且直线上的字母按字典序依次减小，直到大写字母A。
矩阵的其它位置用英文句号．填充。

思路:找规律题

n=int(input().strip())
for i in range(n-1):
    for j in range(i):
        print('.',end='')
    print(chr(ord('A')+i),end='')
    for j in range((2*n-4-2*i)//2):
        print('.',end='')
    print(chr(ord('A')+i),end='')
    for j in range((2*n-4-2*i)//2):
        print('.',end='')
    print(chr(ord('A')+i),end='')
    for j in range(i):
        print('.',end='')
    print()
for i in range(n):
    print(chr(ord('A')+i),end='')
for i in range(n-2,-1,-1):
    print(chr(ord('A')+i),end='')
print()
for i in range(n-2,-1,-1):
    for j in range(i):
        print('.',end='')
    print(chr(ord('A')+i),end='')
    for j in range((2*n-4-2*i)//2):
        print('.',end='')
    print(chr(ord('A')+i),end='')
    for j in range((2*n-4-2*i)//2):
        print('.',end='')
    print(chr(ord('A')+i),end='')
    for j in range(i):
        print('.',end='')
    print()

十六.比赛安排

设有有2^n（n<=6）个球队进行单循环比赛，计划在2^n–1天内完成，每个队每天进行一场比赛。设计一个比赛的安排，使在2^n–1天内每个队都与不同的对手比赛。

思路:深度优先搜索遍历,利用set记录已经遍历过的组合(只能保存元组),再用字典保存当天已经遍历过的人

from collections import defaultdict
n=int(input().strip())
s=set()
def dfs(day):
    global n,s
    d=defaultdict(int)
    if day==2**n:
        return
    print("<{}>".format(day),end='')
    for i in range(1,2**n):
        for j in range(i+1,2**n+1):
            if not (i,j) in s and d[i]==0 and d[j]==0 :  ##集合里面只能跟元组
                d[i]=1
                d[j]=1
                s.add((i,j))
                print("{}-{}".format(i,j),end=' ')
                break
    print()
    dfs(day+1)
dfs(1)

十七.分考场

n个人参加某项特殊考试。
为了公平，要求任何两个认识的人不能分在同一个考场。
求是少需要分几个考场才能满足条件。

思路:图的染色问题,利用dfs,对于每一个人可以分为加入已经存在的考场(如果不冲突)和新加一个考场的两类选择,如果遍历的房间数大于之前保存的答案则剪枝

n=int(input().strip())
m=int(input().strip())
road=[[0 for i in range(n)] for j in range(n)]
flag=[[-1 for j in range(n)] for i in range(n)]
for i in range(m):
    ii,jj=map(int,input().strip().split())
    road[ii-1][jj-1]=1
    road[jj-1][ii-1]=1
ans=n
def dfs(num,room):
    global n,ans,flag
    if room>=ans:
        return
    if num==n:
        if room

十八.小数第n位

我们知道，整数做除法时，有时得到有限小数，有时得到无限循环小数。
如果我们把有限小数的末尾加上无限多个0，它们就有了统一的形式。
本题的任务是：在上面的约定下，求整数除法小数点后的第n位开始的3位数。

思路:分为三种情况:1.不存在循环 2.循环小数但是不从第一位开始循环 3.循环小数且从第一位循环

求出循环节对n取余数,输出答案

from collections import defaultdict
a,b,n=map(int,input().strip().split())
a=a%b
string=defaultdict(int)
ans=''
flag=True
jie=[]
while True:
    c=str(a*10//b)
    a=a*10%b
    if string[a]==1:

        if c==ans[0]:#循环从第一位开始
            jie=ans[ans.index(c):]
            ans=ans[:ans.index(c)]
        else:#循环不从第一位开始
            ans+=c
            jie=ans[ans.index(str(a*10//b)):]
            ans=ans[:ans.index(str(a*10//b))]
        break
    else:
        string[a]=1
        ans+=c
        if a==0:
            flag=False
            break
n-=1


if flag:
    if n>=len(ans):
        n=(n-len(ans))%len(jie)
        print("{}{}{}".format(jie[n],jie[(n+1)%len(jie)],jie[(n+2)%len(jie)]))
    else:
        n = n % len(ans)
        ans+=jie
        print("{}{}{}".format(ans[n],ans[(n+1)],ans[(n+2)]))
else:
    for ii in range(3):
        if n+ii

十九.奇怪的数列

从X星截获一份电码，是一些数字，如下：
13
1113
3113
132113
1113122113
....
YY博士经彻夜研究，发现了规律：
第一行的数字随便是什么，以后每一行都是对上一行“读出来”
比如第2行，是对第1行的描述，意思是：1个1，1个3，所以是：1113
第3行，意思是：3个1,1个3，所以是：3113
请你编写一个程序，可以从初始数字开始，连续进行这样的变换。

s=input().strip()
n=int(input().strip())
def change(s):
    ans=''
    num=s[0]
    temp_num=0
    for i in s:
        if i==num:
            temp_num+=1
        else:
            ans+=str(temp_num)
            ans+=num
            num=i
            temp_num=1
    ans+=str(temp_num)
    ans+=num
    return ans
for j in range(n):
    s=change(s)
print(s)

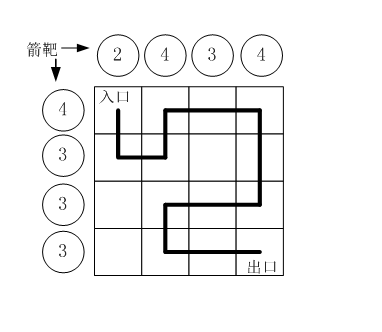
二十.路径之谜

小明冒充X星球的骑士，进入了一个奇怪的城堡。城堡里边什么都没有，只有方形石头铺成的地面。
假设城堡地面是 n x n 个方格。【如图1.png】所示。
按习俗，骑士要从西北角走到东南角。
可以横向或纵向移动，但不能斜着走，也不能跳跃。
每走到一个新方格，就要向正北方和正西方各射一箭。
（城堡的西墙和北墙内各有 n 个靶子）

同一个方格只允许经过一次。但不必走完所有的方格。
如果只给出靶子上箭的数目，你能推断出骑士的行走路线吗？
有时是可以的，比如图1.png中的例子。
本题的要求就是已知箭靶数字，求骑士的行走路径（测试数据保证路径唯一）

思路:dfs剪枝回溯

N=int(input().strip())
up=list(map(int,input().strip().split()))
left=list(map(int,input().strip().split()))
ans=[]
def dfs(i,j):
    global N,up,left,ans
    if up[j]==0 or left[i]==0:
        return
    else:
        up[j]-=1
        left[i]-=1
        if sum(up) == 0 and sum(left) == 0:
            if i==N-1 and j==N-1:
                for ii in ans:
                    print(ii, end=' ')
            return
        if i > 0:
            if (i - 1) * N + j not in ans:
                ans.append((i - 1) * N + j)
                dfs(i - 1, j)
                ans.pop()
        if j > 0:
            if i * N + j - 1 not in ans:
                ans.append(i * N + j - 1)
                dfs(i, j - 1)
                ans.pop()
        if i < N - 1:
            if (i + 1) * N + j not in ans:
                ans.append((i + 1) * N + j)
                dfs(i + 1, j)
                ans.pop()
        if j < N - 1:
            if i * N + j + 1 not in ans:
                ans.append(i * N + j + 1)
                dfs(i, j + 1)
                ans.pop()
        up[j]+=1
        left[i]+=1
ans.append(0)
dfs(0,0)