LeetCode 第 55 场双周赛 / 第 247 场周赛
第 55 场双周赛
1909. 删除一个元素使数组严格递增
题目描述
给你一个下标从 0 开始的整数数组 nums ,如果 恰好 删除 一个 元素后,数组 严格递增 ,那么请你返回 true ,否则返回 false 。如果数组本身已经是严格递增的,请你也返回 true 。
数组 nums 是 严格递增 的定义为:对于任意下标的 1 <= i < nums.length 都满足 nums[i - 1] < nums[i] 。
示例 1:
输入:nums = [1,2,10,5,7]
输出:true
解释:从 nums 中删除下标 2 处的 10 ,得到 [1,2,5,7] 。
[1,2,5,7] 是严格递增的,所以返回 true 。
示例 2:
输入:nums = [2,3,1,2]
输出:false
解释:
[3,1,2] 是删除下标 0 处元素后得到的结果。
[2,1,2] 是删除下标 1 处元素后得到的结果。
[2,3,2] 是删除下标 2 处元素后得到的结果。
[2,3,1] 是删除下标 3 处元素后得到的结果。
没有任何结果数组是严格递增的,所以返回 false 。
示例 3:
输入:nums = [1,1,1]
输出:false
解释:删除任意元素后的结果都是 [1,1] 。
[1,1] 不是严格递增的,所以返回 false 。
示例 4:
输入:nums = [1,2,3]
输出:true
解释:[1,2,3] 已经是严格递增的,所以返回 true 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/remove-one-element-to-make-the-array-strictly-increasing
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
我当时的思路就是真的将一个数删除,然后判断是否是严格递增的
因为我当时想的,如果要在一个数组中跳过一个数来判断是否严格递增有点麻烦,所以就直接暴力了
现在想来,如果找到一组不满足条件的数对,分别删除一次判断就好了,不用每一个数都删除哈哈
class Solution {
public boolean canBeIncreasing(int[] nums) {
int l = nums.length;
if(check(nums))
return true;
for(int i = 0; i < l; i++){
int[] temp = new int[l - 1];
for(int j = 0; j < l - 1; j++){
if(j < i)
temp[j] = nums[j];
if(j >= i)
temp[j] = nums[j + 1];
}
if(check(temp))
return true;
}
return false;
}
public boolean check(int[] nums){
int l = nums.length;
for(int i = 0; i < l - 1; i++){
if(nums[i] >= nums[i + 1])
return false;
}
return true;
}
}
学习一下官解中如何删除一个数,判断数组是否递增的方法
class Solution {
public boolean canBeIncreasing(int[] nums) {
int l = nums.length;
for(int i = 0; i < l - 1; i++){
if(nums[i] >= nums[i + 1])
return check(nums, i) || check(nums, i + 1);
}
return true;
}
//跳过index检查是否严格递增,学习一下官解给的方法
public boolean check(int[] nums, int index){
for(int i = 0; i < nums.length - 2; i++){
int pre = i;
//如果pre下标大于等于index,那么就加一,相当于跳过index
if(pre >= index)
pre += 1;
int curr = i + 1;
//如果curr下标大于等于index,那么就加一,相当于跳过index
if(curr >= index)
curr += 1;
if(nums[pre] >= nums[curr])
return false;
}
return true;
}
}
1910. 删除一个字符串中所有出现的给定子字符串
题目描述
给你两个字符串 s 和 part ,请你对 s 反复执行以下操作直到 所有 子字符串 part 都被删除:
找到 s 中 最左边 的子字符串 part ,并将它从 s 中删除。
请你返回从 s 中删除所有 part 子字符串以后得到的剩余字符串。
一个 子字符串 是一个字符串中连续的字符序列。
示例 1:
输入:s = "daabcbaabcbc", part = "abc"
输出:"dab"
解释:以下操作按顺序执行:
- s = "daabcbaabcbc" ,删除下标从 2 开始的 "abc" ,得到 s = "dabaabcbc" 。
- s = "dabaabcbc" ,删除下标从 4 开始的 "abc" ,得到 s = "dababc" 。
- s = "dababc" ,删除下标从 3 开始的 "abc" ,得到 s = "dab" 。
此时 s 中不再含有子字符串 "abc" 。
示例 2:
输入:s = "axxxxyyyyb", part = "xy"
输出:"ab"
解释:以下操作按顺序执行:
- s = "axxxxyyyyb" ,删除下标从 4 开始的 "xy" ,得到 s = "axxxyyyb" 。
- s = "axxxyyyb" ,删除下标从 3 开始的 "xy" ,得到 s = "axxyyb" 。
- s = "axxyyb" ,删除下标从 2 开始的 "xy" ,得到 s = "axyb" 。
- s = "axyb" ,删除下标从 1 开始的 "xy" ,得到 s = "ab" 。
此时 s 中不再含有子字符串 "xy" 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/remove-all-occurrences-of-a-substring
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这个我还是模拟做的,在字符串匹配时,也是暴力法写的,没有用其他方法,因为觉得是第二题,应该没那么麻烦
class Solution {
int l;
int n;
public String removeOccurrences(String s, String part) {
l = s.length();
n = part.length();
int index = helper(s, part);
while(index != -1){
s = s.substring(0, index) + s.substring(index + n, l);
l -= n;
index = helper(s, part);
}
return s;
}
public int helper(String s, String part){
if(l < n)
return -1;
int i = 0;
int j = 0;
while(i <= l - n){
if(s.charAt(i) != part.charAt(j)){
i++;
}
else{
while(i < l && s.charAt(i) == part.charAt(j)){
i++;
j++;
if(j == n)
return i - n;
}
i = i - j + 1;
j = 0;
}
}
return -1;
}
}
调用自带的方法
class Solution {
public String removeOccurrences(String s, String part) {
while (s.contains(part)) {
int i = s.indexOf(part);
s = s.substring(0, i) + s.substring(i + part.length());
}
return s;
}
}
复习一下KMP算法的写法,主要是next数组的获取
class Solution {
public int strStr(String haystack, String needle) {
int n = haystack.length(), m = needle.length();
if (m == 0) {
return 0;
}
//预处理next数组
int[] next = new int[m];
for (int i = 1, j = 0; i < m; i++) {
//如果匹配不成功,就在之前匹配成功的部分找是否有相同的前后缀
while (j > 0 && needle.charAt(i) != needle.charAt(j)) {
j = next[j - 1];
}
//如果相同,就继续向后匹配
if (needle.charAt(i) == needle.charAt(j)) {
j++;
}
next[i] = j;
}
//原字符串和模式串匹配过程
for (int i = 0, j = 0; i < n; i++) {
//如果匹配不成功,找之前匹配成功的部分是否有相同的前后缀,然后从相同前缀部分继续匹配
while (j > 0 && haystack.charAt(i) != needle.charAt(j)) {
j = next[j - 1];
}
//如果匹配成功,继续向后匹配
if (haystack.charAt(i) == needle.charAt(j)) {
j++;
}
if (j == m) {
return i - m + 1;
}
}
return -1;
}
}
1911. 最大子序列交替和
题目描述
一个下标从 0 开始的数组的 交替和 定义为 偶数 下标处元素之 和 减去 奇数 下标处元素之 和 。
比方说,数组 [4,2,5,3] 的交替和为 (4 + 5) - (2 + 3) = 4 。
给你一个数组 nums ,请你返回 nums 中任意子序列的 最大交替和 (子序列的下标 重新 从 0 开始编号)。
一个数组的 子序列 是从原数组中删除一些元素后(也可能一个也不删除)剩余元素不改变顺序组成的数组。比方说,[2,7,4] 是 [4,2,3,7,2,1,4] 的一个子序列(加粗元素),但是 [2,4,2] 不是。
示例 1:
输入:nums = [4,2,5,3]
输出:7
解释:最优子序列为 [4,2,5] ,交替和为 (4 + 5) - 2 = 7 。
示例 2:
输入:nums = [5,6,7,8]
输出:8
解释:最优子序列为 [8] ,交替和为 8 。
示例 3:
输入:nums = [6,2,1,2,4,5]
输出:10
解释:最优子序列为 [6,1,5] ,交替和为 (6 + 5) - 1 = 10 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-alternating-subsequence-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这个题读了以后,就想到怎么才能使这个交替和最大呢,就是找左边元素大于右边元素的数对,然后将这些数组的两个数之差加起来,当然,最后一个数对要特殊处理,因为这时,不减去最后一个数交替和是更大的,所以在最后结果加上最后减去的数就行了
那么如何使一个数对最大呢,就是在一个数的右边,找比它小的最小的数
报了一次错,数据超int了。。下次再仔细点
class Solution {
public long maxAlternatingSum(int[] nums) {
//就是说两个一组,左边元素大于右边元素就保留
//感觉像是单调栈,从左往右遍历,如果小于当前数
//就是找一个数,右边比它小的最小数,如果后面没有符合要求的数对的话
int l = nums.length;
int i = 0;
long res = 0;
while(i < l - 1){
//如果左边数大于右边数,那么说明可以有一个这样的数对
if(nums[i] > nums[i + 1]){
long temp = nums[i];
long min = nums[i + 1];
//要查找最小数的范围是从i + 2开始
i = i + 2;
while(i < l - 1){
//如果发现有左边数大于右边数的数对了,并且要比min大,就跳出循环
//因为如果比min小的话,单独提取出来并不会使交替和更大
//例如,单调递减的序列,8 6 4 2
if(nums[i] > nums[i + 1] && nums[i] > min)
break;
min = Math.min(min, nums[i]);
i++;
}
//因为取不到最后一个值,所以需要对最后一个值进行处理
if(i == l - 1)
min = Math.min(min, nums[i]);
res += temp - min;
//如果没有左边大于右边的数对,那么就一直往后判断
}else{
i++;
}
}
//最后加上最后一个值
res += nums[l - 1];
return res;
}
}
看了大佬们的思路,感觉自己是个fw
首先是贪心,这个题就相当于在最高的时候买入股票,在最低的时候卖出,然后可以买卖无数次
class Solution {
public long maxAlternatingSum(int[] nums) {
//贪心
int n = nums.length;
long res = 0;
int pre = nums[0];
for(int i = 1; i < n; i++){
//如果比之前买入价格小,就卖出,然后再把当前股票买入
if(nums[i] < pre){
res += pre - nums[i];
pre = nums[i];
//如果大于之前买入的价格,就换成新的价格
}else{
pre = nums[i];
}
}
//最后相当于有一个0,需要将最后买入的股票卖出
return res + pre;
}
}
动规:
odd[i] 表示在数组nums 的前缀nums[0…i] 中选择元素组成子序列,且最后一个选择的元素的下标是奇数时,可以得到的最大交替和。
even[i] 表示在nums[0…i] 中选择元素组成子序列,且最后一个选择的元素的下标是偶数时,可以得到的最大交替和。
对于odd而言,如果选择nums[i],因为最后一个元素下标是奇数,所以odd[i] = max{odd[i - 1], even[i - 1] - nums[i]};
对于even而言,如果选择nums[i],因为最后一个元素下标是偶数,所以even[i] = max{even[i - 1], even[i - 1] + nums[i]};
最后结果最后一个元素下标肯定是偶数,所以结果就是even[l - 1]
class Solution {
public long maxAlternatingSum(int[] nums) {
//动规
int l = nums.length;
long[] odd = new long[l];
long[] even = new long[l];
even[0] = nums[0];
for(int i = 1; i < l; i++){
odd[i] = Math.max(odd[i - 1], even[i - 1] - nums[i]);
even[i] = Math.max(even[i - 1], odd[i - 1] + nums[i]);
}
return even[l - 1];
}
}
1912. 设计电影租借系统
题目描述
你有一个电影租借公司和 n 个电影商店。你想要实现一个电影租借系统,它支持查询、预订和返还电影的操作。同时系统还能生成一份当前被借出电影的报告。
所有电影用二维整数数组 entries 表示,其中 entries[i] = [shopi, moviei, pricei] 表示商店 shopi 有一份电影 moviei 的拷贝,租借价格为 pricei 。每个商店有 至多一份 编号为 moviei 的电影拷贝。
系统需要支持以下操作:
Search:找到拥有指定电影且 未借出 的商店中 最便宜的 5 个 。商店需要按照 价格 升序排序,如果价格相同,则 shopi 较小 的商店排在前面。如果查询结果少于 5 个商店,则将它们全部返回。如果查询结果没有任何商店,则返回空列表。
Rent:从指定商店借出指定电影,题目保证指定电影在指定商店 未借出 。
Drop:在指定商店返还 之前已借出 的指定电影。
Report:返回 最便宜的 5 部已借出电影 (可能有重复的电影 ID),将结果用二维列表 res 返回,其中 res[j] = [shopj, moviej] 表示第 j 便宜的已借出电影是从商店 shopj 借出的电影 moviej 。res 中的电影需要按 价格 升序排序;如果价格相同,则 shopj 较小 的排在前面;如果仍然相同,则 moviej 较小 的排在前面。如果当前借出的电影小于 5 部,则将它们全部返回。如果当前没有借出电影,则返回一个空的列表。
请你实现 MovieRentingSystem 类:
MovieRentingSystem(int n, int[][] entries) 将 MovieRentingSystem 对象用 n 个商店和 entries 表示的电影列表初始化。
List search(int movie) 如上所述,返回 未借出 指定 movie 的商店列表。
void rent(int shop, int movie) 从指定商店 shop 借出指定电影 movie 。
void drop(int shop, int movie) 在指定商店 shop 返还之前借出的电影 movie 。
List> report() 如上所述,返回最便宜的 已借出 电影列表。
注意:测试数据保证 rent 操作中指定商店拥有 未借出 的指定电影,且 drop 操作指定的商店 之前已借出 指定电影。
示例 1:
输入:
["MovieRentingSystem", "search", "rent", "rent", "report", "drop", "search"]
[[3, [[0, 1, 5], [0, 2, 6], [0, 3, 7], [1, 1, 4], [1, 2, 7], [2, 1, 5]]], [1], [0, 1], [1, 2], [], [1, 2], [2]]
输出:
[null, [1, 0, 2], null, null, [[0, 1], [1, 2]], null, [0, 1]]
解释:
MovieRentingSystem movieRentingSystem = new MovieRentingSystem(3, [[0, 1, 5], [0, 2, 6], [0, 3, 7], [1, 1, 4], [1, 2, 7], [2, 1, 5]]);
movieRentingSystem.search(1); // 返回 [1, 0, 2] ,商店 1,0 和 2 有未借出的 ID 为 1 的电影。商店 1 最便宜,商店 0 和 2 价格相同,所以按商店编号排序。
movieRentingSystem.rent(0, 1); // 从商店 0 借出电影 1 。现在商店 0 未借出电影编号为 [2,3] 。
movieRentingSystem.rent(1, 2); // 从商店 1 借出电影 2 。现在商店 1 未借出的电影编号为 [1] 。
movieRentingSystem.report(); // 返回 [[0, 1], [1, 2]] 。商店 0 借出的电影 1 最便宜,然后是商店 1 借出的电影 2 。
movieRentingSystem.drop(1, 2); // 在商店 1 返还电影 2 。现在商店 1 未借出的电影编号为 [1,2] 。
movieRentingSystem.search(2); // 返回 [0, 1] 。商店 0 和 1 有未借出的 ID 为 2 的电影。商店 0 最便宜,然后是商店 1 。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/design-movie-rental-system
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
思路可能不太难,就是写起来麻烦,细节比较多,我这里直接借鉴了,加了点注释
class MovieRentingSystem {
//键为电影,值为以价格和商店排序的优先队列,方便租借
Map<Integer, PriorityQueue<int[]>> movies = new HashMap<>();
//表示借出去的电影元素
Set<int[]> set = new HashSet<>();
//借出去的电影
PriorityQueue<int[]> jie = new PriorityQueue<>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {
//首先按价格排序
if(o1[2] != o2[2])
return o1[2]-o2[2];
//再按商店排序
else if(o1[0] != o2[0])
return o1[0]-o2[0];
//再按movie排序
else
return o1[1]-o2[1];
}
});
//存储每个商店的电影
Map<Integer, int[]>[] shops;
public MovieRentingSystem(int n, int[][] entries) {
//有n个商店,就有n个Map
shops = new Map[n];
for(int i = 0; i < n; i++)
shops[i]= new HashMap();
//将电影加入商店哈希表中
for(int i = 0; i < entries.length; i++){
//当前电影元素
int[] tem = entries[i];
//如果当前电影没有存储到优先队列中,那么创建当前电影的优先队列
if(movies.get(tem[1]) == null)
movies.put(tem[1], new PriorityQueue<>(new Comparator<int[]>() {
@Override
//按照电影价格、商店从小较大排序
public int compare(int[] o1, int[] o2) {
if(o1[2] != o2[2])
return o1[2] - o2[2];
else return o1[0]-o2[0];
}
}));
//在当前电影的队列中添加当前电影元素
movies.get(tem[1]).add(tem);
//当前商店中的电影
shops[tem[0]].put(tem[1], tem);
}
}
public List<Integer> search(int movie) {
int num = 5;
List<Integer> list = new ArrayList<>();
if(movies.get(movie) == null)
return list;
//取得当前电影的优先队列
PriorityQueue<int[]> tem = (movies.get(movie));
//用栈存储被弹出的电影元素
Stack<int[]> stack = new Stack<>();
//如果队列不等于空
while (!tem.isEmpty() && num > 0){
//弹出当前电影元素
int[] arr = tem.poll();
//存储到栈中
stack.add(arr);
//如果当前电影元素没有被租借,就加入list中
if(!set.contains(arr)) {
list.add(arr[0]);
num--;
}
}
//重新加入优先队列
while (!stack.isEmpty())
tem.add(stack.pop());
return list;
}
//租借,租借的电影元素加到set集合中,同时也加到jie集合中
public void rent(int shop, int movie) {
//获得当前元素
int[] tem = shops[shop].get(movie);
//加到set集合中
set.add(tem);
jie.add(tem);
}
//归还
public void drop(int shop, int movie) {
//取出归还的电影
int[] tem = shops[shop].get(movie);
//从set和jie中移除
set.remove(tem);
jie.remove(tem);
}
//取出借出去的最便宜的5部电影
public List<List<Integer>> report() {
int num = 5;
PriorityQueue<int[]> tem = jie;
List<List<Integer>> list = new ArrayList<>();
Stack<int[]> stack = new Stack<>();
while (!tem.isEmpty() && num > 0){
int[] arr = tem.poll();
stack.add(arr);
//将数组变成list
List<Integer> ll = new ArrayList<>();
ll.add(arr[0]);
ll.add(arr[1]);
list.add(ll);
num--;
}
while (!stack.isEmpty())
jie.add(stack.pop());
return list;
}
}
这场周赛咋说呢,做出来三道题其实还是挺开心的,排名也在850之前,也算进步吧,但是今天看了题解,发现所用的方法都不是最优的,然后导致所用时间比较长吧,也就导致最后没有时间看最后一道题了,其实最后一道题本身思路不难,就可能需要花时间写代码,还需努力
第 247 场周赛
有一说一,这场周赛感觉很难,就做出来两道但是排名还是800多哈哈
1913. 两个数对之间的最大乘积差
题目描述
两个数对 (a, b) 和 (c, d) 之间的 乘积差 定义为 (a * b) - (c * d) 。
例如,(5, 6) 和 (2, 7) 之间的乘积差是 (5 * 6) - (2 * 7) = 16 。
给你一个整数数组 nums ,选出四个 不同的 下标 w、x、y 和 z ,使数对 (nums[w], nums[x]) 和 (nums[y], nums[z]) 之间的 乘积差 取到 最大值 。
返回以这种方式取得的乘积差中的 最大值 。
示例 1:
输入:nums = [5,6,2,7,4]
输出:34
解释:可以选出下标为 1 和 3 的元素构成第一个数对 (6, 7) 以及下标 2 和 4 构成第二个数对 (2, 4)
乘积差是 (6 * 7) - (2 * 4) = 34
示例 2:
输入:nums = [4,2,5,9,7,4,8]
输出:64
解释:可以选出下标为 3 和 6 的元素构成第一个数对 (9, 8) 以及下标 1 和 5 构成第二个数对 (2, 4)
乘积差是 (9 * 8) - (2 * 4) = 64
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/maximum-product-difference-between-two-pairs
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
这个很简单,直接排序,后两个数相乘减前两个数就好了,这样写复杂度不是最优,但是写起来快,竞赛的时候这样写最好
class Solution {
public int maxProductDifference(int[] nums) {
int l = nums.length;
Arrays.sort(nums);
return nums[l - 1] * nums[l - 2] - nums[0] * nums[1];
}
}
1914. 循环轮转矩阵
题目描述
给你一个大小为 m x n 的整数矩阵 grid ,其中 m 和 n 都是 偶数 ;另给你一个整数 k 。
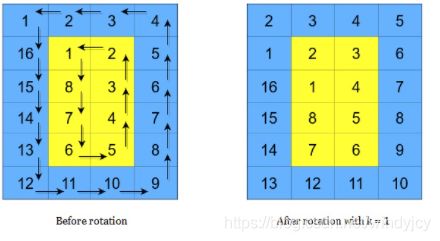
矩阵由若干层组成,如下图所示,每种颜色代表一层:
矩阵的循环轮转是通过分别循环轮转矩阵中的每一层完成的。在对某一层进行一次循环旋转操作时,层中的每一个元素将会取代其 逆时针 方向的相邻元素。轮转示例如下:
返回执行 k 次循环轮转操作后的矩阵。
示例 1:
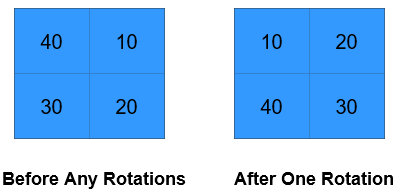
输入:grid = [[40,10],[30,20]], k = 1
输出:[[10,20],[40,30]]
解释:上图展示了矩阵在执行循环轮转操作时每一步的状态。
示例 2:
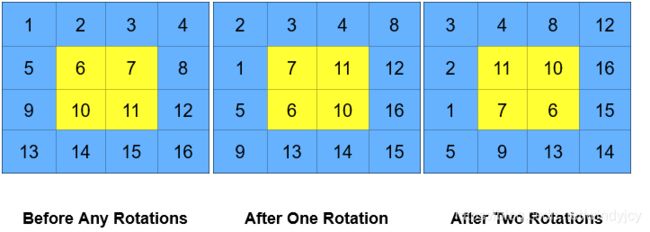
输入:grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2
输出:[[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]]
解释:上图展示了矩阵在执行循环轮转操作时每一步的状态。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/cyclically-rotating-a-grid
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
又是矩阵的操作,这次要好好看看背一个简洁的代码
竞赛中我是将每一圈移动相应的次数得到的结果,代码写了很久,而且还很容易出错
class Solution {
public int[][] rotateGrid(int[][] grid, int k) {
int m = grid.length;
int n = grid[0].length;
int t = m < n ? m /2 : n / 2;
//最外面的圈
int z = k % (2 * m + 2 * n - 4);
//找到第一个位置应该在的点,就是移动k次
for(int i = 0; i < t; i++){
z = k % (2 * m + 2 * n - 4);
int[][] temp = new int[grid.length][grid[0].length];
for(int j = 0; j < z; j++){
if(j == 0)
temp = rotate(grid, i);
else
temp = rotate(temp, i);
}
for(int x = 0; x < grid.length; x++){
for(int y = 0; y < grid[0].length; y++){
if(temp[x][y] != 0)
grid[x][y] = temp[x][y];
}
}
m -= 2;
n -= 2;
}
return grid;
}
public int[][] rotate(int[][] grid, int t){
int m = grid.length;
int n = grid[0].length;
int[][] temp = new int[m][n];
for(int i = t; i < m - 1 - t; i++){
temp[i + 1][t] = grid[i][t];
}
for(int i = t; i < n - 1 - t; i++){
temp[m - 1 - t][i + 1] = grid[m - 1 - t][i];
}
for(int i = m - 1 - t; i > t; i--){
temp[i - 1][n - 1 - t] = grid[i][n - 1 - t];
}
for(int i = n - 1 - t; i > t; i--){
temp[t][i - 1] = grid[t][i];
}
return temp;
}
}
看了一圈,好像也没有特别简单的代码…也是分层,然后旋转,只不过旋转的代码有的不一样
这里旋转的时候,可以不用创建一个新的数组来进行拷贝,而可以保存第一个点,然后将其他点依次进行旋转
class Solution {
public int[][] rotateGrid(int[][] grid, int k) {
int m = grid.length;
int n = grid[0].length;
int t = m < n ? m /2 : n / 2;
//找到第一个位置应该在的点,就是移动k次
for(int i = 0; i < t; i++){
int z = k % (2 * m + 2 * n - 4);
grid = rotate(grid, i, z);
m -= 2;
n -= 2;
}
return grid;
}
public int[][] rotate(int[][] grid, int t, int k){
int m = grid.length;
int n = grid[0].length;
//因为将第一个位置空出来了,所以需要先填充第一个位置,所以顺序也就变成了上,右,下,左
while(k-- > 0){
int head = grid[t][t];
for(int i = t; i < n - 1 - t; i++){
grid[t][i] = grid[t][i + 1];
}
for(int i = t; i < m - t - 1; i++){
grid[i][n - 1 - t] = grid[i + 1][n - 1 - t];
}
for(int i = n - 1 - t; i > t; i--){
grid[m - 1 - t][i] = grid[m - 1 - t][i - 1];
}
for(int i = m - 1 - t; i > t; i--){
grid[i][t] = grid[i - 1][t];
}
grid[t + 1][t] = head;
}
return grid;
}
}
还有这种将每一圈的数先放在一个数组中,然后对数组进行操作,
将数组中的元素放入双向队列中,每次旋转就是把队首的数取出来放在队尾,旋转k次
最后再将数组还原成矩阵
class Solution {
public int[][] rotateGrid(int[][] grid, int k) {
// 矩阵尺寸
int m = grid.length, n = grid[0].length;
// 计算一共有多少层
int layerNumber = Math.min(m, n) / 2;
// 逐层处理
for (int i = 0; i < layerNumber; ++i) {
// 计算出来当前层需要多大的数组来存放, 计算方法是当前层最大尺寸 - 内部下一层尺寸.
int[] data = new int[(m - 2 * i) * (n - 2 * i) - (m - (i + 1) * 2) * (n - (i + 1) * 2)];
int idx = 0;
// 从左往右
for (int offset = i; offset < n - i - 1; ++offset)
data[idx++] = grid[i][offset];
// 从上往下
for (int offset = i; offset < m - i - 1; ++offset)
data[idx++] = grid[offset][n - i - 1];
// 从右往左
for (int offset = n - i - 1; offset > i; --offset)
data[idx++] = grid[m - i - 1][offset];
// 从下往上
for (int offset = m - i - 1; offset > i; --offset)
data[idx++] = grid[offset][i];
// 把旋转完的放回去
Integer[] ret = rotateVector(data, k);
idx = 0;
// 从左往右
for (int offset = i; offset < n - i - 1; ++offset)
grid[i][offset] = ret[idx++];
// 从上往下
for (int offset = i; offset < m - i - 1; ++offset)
grid[offset][n - i - 1] = ret[idx++];
// 从右往左
for (int offset = n - i - 1; offset > i; --offset)
grid[m - i - 1][offset] = ret[idx++];
// 从下往上
for (int offset = m - i - 1; offset > i; --offset)
grid[offset][i] = ret[idx++];
}
return grid;
}
private Integer[] rotateVector(int[] vector, int offset) {
// 取余, 否则会有无用功, 超时
offset = offset % vector.length;
Deque<Integer> deque = new ArrayDeque<>();
for (int item : vector) deque.add(item);
// 旋转操作
while (offset-- > 0) {
deque.addLast(deque.pollFirst());
}
//学习这个队列转变成数组的方法, T[] toArray(T[] a)
//a - the array into which the elements of this collection are to be stored, if it is big enough; otherwise, a new array of the same runtime type is allocated for this purpose.
//意思就是后面这个参数是一个标准,如果这个数组够大,就存储在这个里面,否则,就创建一个新的同类型的数组来存储
return deque.toArray(new Integer[0]);
}
}
作者:hxz1998
链接:https://leetcode-cn.com/problems/cyclically-rotating-a-grid/solution/java-si-lu-ju-jian-dan-fen-zu-xuan-zhuan-0rqj/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
1915. 最美子字符串的数目
题目描述
如果某个字符串中 至多一个 字母出现 奇数 次,则称其为 最美 字符串。
例如,"ccjjc" 和 "abab" 都是最美字符串,但 "ab" 不是。
给你一个字符串 word ,该字符串由前十个小写英文字母组成('a' 到 'j')。请你返回 word 中 最美非空子字符串 的数目。如果同样的子字符串在 word 中出现多次,那么应当对 每次出现 分别计数。
子字符串 是字符串中的一个连续字符序列。
示例 1:
输入:word = "aba"
输出:4
解释:4 个最美子字符串如下所示:
- "aba" -> "a"
- "aba" -> "b"
- "aba" -> "a"
- "aba" -> "aba"
示例 2:
输入:word = "aabb"
输出:9
解释:9 个最美子字符串如下所示:
- "aabb" -> "a"
- "aabb" -> "aa"
- "aabb" -> "aab"
- "aabb" -> "aabb"
- "aabb" -> "a"
- "aabb" -> "abb"
- "aabb" -> "b"
- "aabb" -> "bb"
- "aabb" -> "b"
示例 3:
输入:word = "he"
输出:2
解释:2 个最美子字符串如下所示:
- "he" -> "h"
- "he" -> "e"
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/number-of-wonderful-substrings
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
竞赛的时候写了个前缀和然后遍历所有子串的超时的代码,然后不知道怎么优化了
这个题的思想需要好好学习一下:
首先,因为只关心每个字母出现的奇偶性,而字母也只统计a到j , 因此可以用一个长度为10的二进制数来表示每个字母的出现次数的奇偶性,这是第一点,状态压缩
再考虑前缀和,由于只考虑奇偶性,所以计算前缀和可以由加法改成异或运算,异或运算又被称为不进位加法,正好和奇偶性对应,0为偶,1为奇
进行一次遍历,边遍历边处理前缀和,如果有两个前缀和相同,则这两个前缀和的异或结果为0,也就是说对应子串中的每个字母的个数为偶数。我们需要存储用一个数据结构来存储之前遍历到的前缀和,以及它出现的次数,这里因为10个二进制位共1024种情况,可以用一个1024个长度的数组来存储每个前缀和出现的次数
题目中还有一个要求就是允许有一个字母出现奇数次,因此对于当前前缀和,我们还可以找有一位和它不一样的前缀和。我们可以对当前前缀和的10位进行枚举,并对其中一位进行反转,然后查询它出现的次数并加入最后的结果中
总结一下这个题的思想,首先是将出现次数的奇偶性转变成0 1的二进制串
然后边遍历边处理,用哈希表存储已经出现过的二进制串,这个操作其实在很多处理前缀和的题中都用到了,力扣第一道题两数之和也用到了,之前也专门练了几道这样的题,但是还是难想到…
对于当前需要的二进制串,直接在哈希表中取出来就可以了
class Solution {
public long wonderfulSubstrings(String word) {
int l = word.length();
int[] count = new int[1024];
count[0] = 1;
int mask = 0;
long res = 0;
for(int i = 0; i < l; i++){
char c = word.charAt(i);
int index = c - 'a';
//当前mask
mask ^= (1 << index);
res += count[mask];
//如果有一位不同
for(int j = 0; j < 10; j++){
int mask_re = mask ^ (1 << j);
res += count[mask_re];
}
count[mask]++;
}
return res;
}
}
练习:930. 和相同的二元子数组
题目描述
给你一个二元数组 nums ,和一个整数 goal ,请你统计并有多少个和为 goal 的 非空 子数组。
子数组 是数组的一段连续部分。
示例 1:
输入:nums = [1,0,1,0,1], goal = 2
输出:4
解释:
如下面黑体所示,有 4 个满足题目要求的子数组:
[1,0,1,0,1]
[1,0,1,0,1]
[1,0,1,0,1]
[1,0,1,0,1]
示例 2:
输入:nums = [0,0,0,0,0], goal = 0
输出:15
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-subarrays-with-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
前缀和+哈希表
class Solution {
public int numSubarraysWithSum(int[] nums, int goal) {
int l = nums.length;
int[] pre = new int[l + 1];
int res = 0;
Map<Integer, Integer> map = new HashMap<>();
map.put(0, 1);
for(int i = 0; i < l; i++){
pre[i + 1] = pre[i] + nums[i];
if(map.containsKey(pre[i + 1] - goal))
res += map.get(pre[i + 1] - goal);
map.put(pre[i + 1], map.getOrDefault(pre[i + 1], 0) + 1);
}
return res;
}
}
1916. 统计为蚁群构筑房间的不同顺序(跳了)
题目描述
你是一只蚂蚁,负责为蚁群构筑 n 间编号从 0 到 n-1 的新房间。给你一个 下标从 0 开始 且长度为 n 的整数数组 prevRoom 作为扩建计划。其中,prevRoom[i] 表示在构筑房间 i 之前,你必须先构筑房间 prevRoom[i] ,并且这两个房间必须 直接 相连。房间 0 已经构筑完成,所以 prevRoom[0] = -1 。扩建计划中还有一条硬性要求,在完成所有房间的构筑之后,从房间 0 可以访问到每个房间。
你一次只能构筑 一个 房间。你可以在 已经构筑好的 房间之间自由穿行,只要这些房间是 相连的 。如果房间 prevRoom[i] 已经构筑完成,那么你就可以构筑房间 i。
返回你构筑所有房间的 不同顺序的数目 。由于答案可能很大,请返回对 109 + 7 取余 的结果。
示例 1:
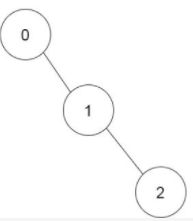
输入:prevRoom = [-1,0,1]
输出:1
解释:仅有一种方案可以完成所有房间的构筑:0 → 1 → 2
示例 2:
输入:prevRoom = [-1,0,0,1,2]
输出:6
解释:
有 6 种不同顺序:
0 → 1 → 3 → 2 → 4
0 → 2 → 4 → 1 → 3
0 → 1 → 2 → 3 → 4
0 → 1 → 2 → 4 → 3
0 → 2 → 1 → 3 → 4
0 → 2 → 1 → 4 → 3
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/count-ways-to-build-rooms-in-an-ant-colony
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路
树状动态规划…还有乘法逆元,排列数的公式,算了,以后有时间再看吧