Spark上的决策树(Decision Tree On Spark)
最近花了一些时间学习了Scala和Spark(版本是1.6.3),学习语言和框架这样的东西,除了自己敲代码折腾和玩弄外,另一个行之有效的方法就是阅读代码。MLlib正好是以Spark为基础的开源机器学习库,便借机学习MLlib是如何利用Spark实现分布式决策树。本文主要是剖析MLlib的DecisionTree源码,假设读者已经入门Scala基本语法,并熟悉决策树的基本概念,假如您不清楚,可以参照Coursera上两门课程,一门是Scala之父Martin Odersky的《Functional Programming Principles in Scala》,用来学习Scala。另一门则是台湾大学林轩田教授的《机器学习技法》,用于学习决策树基础:-)。
实现概要
在陷入实现细节之前,我们先从全局大方面上来把握一下MLlib是如何实现分布式决策树的。
- 首先,MLlib认为,决策树是随机森林(RandomForest)的一种特殊情况,也就是只有一棵树并且不采取特征抽样的随机森林。所以在训练决策树的时候,其实是训练随机森林,最后从随机森林中抽出一棵树。
- 为了减少分布式训练过程中遍历数据的次数和提高训练速度,实现上采取了以下几个优化技巧:
- 以广度优先方式建树(传统的实现是递归版本的深度优先方式)
- 广度优先获得在maxMemory限制下的队列中的节点,作为一组,按组训练,这样每一次遍历数据需要做更多的计算和更多的存储空间,但是相应地减少了网络通信
- 提前计算特征的切割点(Split)和切割区间(Bin),在数据量大的情况下,可以近似按Bin寻找最优切割点,而不用遍历训练数据的所有可能分割点
- 利用已知的Bin和每个Bin需要的统计量个数构造一个一维数组,进行分区统计再合并
优化技巧剖析
训练随机森林获取决策树
其实这算不上什么优化技巧,为了逻辑上连贯,还是加上了:-),什么都不用说,直接上代码,请看DecisionTree中的run方法便知:
def run(input: RDD[LabeledPoint]): DecisionTreeModel = {
// Note: random seed will not be used since numTrees = 1.
val rf = new RandomForest(strategy, numTrees = 1, featureSubsetStrategy = "all", seed = 0)
val rfModel = rf.run(input)
rfModel.trees(0)
}按层建树
其实这个技巧挺简单的,只要你知道如何按层打印二叉树的节点就可以,这种可是经典的面试题来的-:),很简单,只需利用一个队列来辅助即可。每次将队列的节点全部拿出来,按顺序处理每个节点,并将产生的新节点重新进队列,直到队列为空。
queue.enqueue(root)
while !queue.isEmpty:
nodes = extractNodes(queue) //取出队列中的节点
for node in nodes:
growTree(node,queue) //此处子节点可能会进入queue这样便实现了按层建树的过程。MLlib中将这样每一次迭代从queue中获取的节点归为一组,并考虑每一组是需要用到的内存是否满足最大的内存限制,所以并不是每一次迭代都取整层的节点。也就是说每一组可能有不同层次的节点,因为是训练随机森林,所以每一组的节点可能来源不止一棵树。通过分组的操作,每一次遍历数据,可以操作当前组的所有节点,而不是只处理一个节点,从而减少了数据的遍历次数。
提前计算特征的切割点(Split)和切割区间(Bin)
遍历一遍输入数据或采样数据,我们就可以提前知道所有可能的分裂点。决策树的一个优势是可以处理连续特征(Continuous feature)和类别特征(Category feature)。
对于类别特征,比如一个颜色特征,它的特征值可以是:红,黄,蓝,绿。假设一个类别特征的特征值数目为 N ,因为一个特征可以同时取得多个特征值,比如红蓝,蓝绿,那么分割点其实就是特征值的所有可能组合,其个数为:2N,对于二叉决策树而言,有一半的分裂点其实是重复的,比如选红蓝为分割点和选黄绿为分割点其实是一样的,所以必须除以2,也就是 2N−1 ,对于其中一种情况是取得所有特征值或者一种都取不到的情况,必须排除,所以最终的分裂点Split个数就是: 2N−1−1 ,而区间Bin个数就是 2N−2 。具体实现中,MLlib采用了一个可证明的技巧(详请查阅《The Elements Of Statistical Learning》9.2.4节),对于二元分类问题,分裂点Split个数直接设为 N−1 ,Bin的个数为 N 。
对于连续的实数特征,如果数据集很小的情况下,通常会将特征的取值进行排序,然后遍历每个取值,尝试分裂,选出满足信息增益最大或者Gini-index最纯的分裂点。在数据量很大的情况下,对每个可能取值进行排序成本就太大了,一个惯用的近似技巧——“箱化” (Binning,我们觉得取值太多了,一个个处理太麻烦,打包起来,处理就简单多了)。假如原来特征的取值是:
但是对于海量数据,或者一个无序的特征有太多的特征值,就有必要控制Bin的个数了,所以一个近似的做法就是,提前确定好箱子Bin的个数,也就是为什么在决策树设定参数中有maxBins这个参数的来由了。对于类别特征如果特征值超过maxBins,那么将分裂箱子Bin的数量退化为特征值的个数。对于连续的特征,如果不同训练特征少于maxBins,那么还是按照前面分析的做法,如果超过了,Bin的个数就设为maxBins,并采取尽量平均的方式选择切割点,使得每个Bin尽量包含相同个数的训练数据。如果训练数据实在太多,可以使用采样的方式,利用采样部分数据作为训练数据再使用上面的方法确定Split和Bin。由于采取了分区间的操作和可能的采样手段,必然降低了决策树的预测精度,但是另一方面却可以大大提升训练速度。实际中据说这样的技巧也没损伤多少精度-:)。
以上分析位于代码DecisionTreeMetadata.buildMetadata方法和DecisionTree.findSplitsBins方法中。其中DecisionTreeMetadata.buildMetadata设定了无序特征的分裂数目,而DecisionTree.findSplitsBins则确定了连续特征的分裂数并且实际生成连续特征、有序类别特征、无序类别特征的分裂对象(Split)和分裂区间(Bin)
数据切割
正常的决策树算法在某个节点选到最佳split之后,会将数据以此切割成两部分,然后继续递归去寻找分裂节点,对于mllib的决策树实现来说,这种递归实现做法是不可行的,那么如何将数据进行切割呢?其实也很简单,假设此时决策树已经构建了一部分,然后对于一个新的节点,我们想在此节点上通过信息增益或者其他函数选择最优的split,那么如何计算落在该节点的数据呢?一个简单的方式就是模拟决策树的预测过程,一个数据从根节点开始走预测流程,如果最终落到我们目标节点上,那么该数据就是参与接下来计算最佳分裂算法的所需数据之一,mllib上在binSeqOp函数中就是通过predictNodeIndex函数实现对数据的切割的。
按节点分区计算部分统计量
因为Spark的RDD数据是以Partition分区存储的。所以如果能先利用分区计算部分统计量,最后再合并统计量,就可以减少很多不必要的通信开销。那么该怎样分区统计并且使得后面合并的时候方便呢?MLlib的具体实现是为每个节点创建一个一维数组allStats作为统计的容器,怎样一个一维数组呢?由于上一步的计算,我们已经提前知道每个特征对应的Bin的个数了,那么每个Bin里面到底需要多少统计量呢?对于分类问题,假设是二元分类,那么每个Bin其实只有2个统计量,就是计算落到这个Bin里面正负样本的个数。而多类分类问题,分类个数N,则每个Bin里面就需要 N 个统计量。给个图直观展示一下,对于一个3类分类决策树,构造这样的一维数组allStats形式如下:
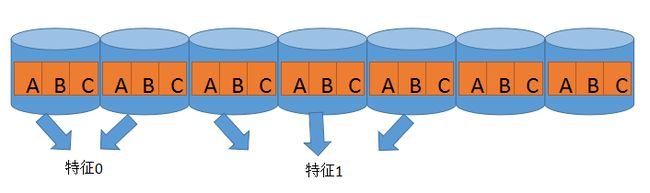
每个Bin都有3个类别的count,并顺序排列下去组成一个大的一维数组。这样的大数组涵盖了我们计算的所有可能性,为每个节点创建这样一个数组,都会消耗一定内存,所以设置maxBins需要小心。
既然我们提前知道每个特征对应的Bin的个数和每个Bin需要的统计量个数,我们可以设置一个数组featureOffsets,大小是featureNum,从0开始,累加每个feature对应的Bin数目,也就是进行Cumulative sum 操作。这样数组最后一个元素值就是总的Bin的个数totalBins。计算featureOffsets的代码如下:
private val featureOffsets: Array[Int] = {
numBins.scanLeft(0)((total, nBins) => total + statsSize * nBins)
}设置这样的偏移数组的好处就是一旦获得featureIndex,我们很方便查询到具体在上面大数组中的偏移量。给定一个featureIndex,还有binIndex,假设每个Bin的统计量为statSize,那么在大数组的更新偏移量为:
整理一下,我们之前已经事先计算每一个特征可能落入的Bin和切割点Split。也就是说一个特征取得不同的值将可能会落入不同的Bin中,但是对应具体的一个训练数据LabeledPoint,在每个特征上的取值已经是确定了,那么对于该LabeledPoint,我们可以事先计算每个特征对应落到那个Bin中,由于我们之前计算连续特征对应的Split和Bin的时候是有序的,那么可以利用二分查找寻找每个具体特征值的对应Bin,这也大大地节约了计算量。对于Categorical特征,则特征值就作为Bin的Index。具体可参考TreePoint的实现。LabeledPoint到TreePoint的转换其实就是将LabeledPoint里面的每一个特征值映射到每个Bin的Index,对于每一个TreePoint,我们因此可以知道它所有落入不同Bin的位置并更新那个Bin的统计量。
这样复杂的计算过程,在MLlib中实现抽象为类DTStatsAggregator,每个节点都有对应的DTStatsAggregator,DTStatsAggregator中包含前面介绍的allStats和featureOffsets。用于计算不同Bin在各个RDD分区的部分统计,最后再由reduceByKey合并起来,变成一个充分统计。示意如下:

因为这个技巧需要综合之前所有技巧,并且为了效率,实现上没有过多抽象,读起源码来难度会比较大。所以读一两遍读不懂不要气馁-:)。在真正分裂节点的时候,Continuous Feature和Categorical Feature是在计算信息增益的形式是有所不同的,并且都运用了Cumulative sum的技巧,但是这已经不是为了实现分布式决策树的技巧,这里就不再赘述。
结语
其实单单靠文字很难表达清楚整个实现过程,但是本文也差不多点出了MLlib中DecisionTree的核心要点,我并不希冀读者通过阅读本文就可以完全理解,但是可以根据本文点出的概念,再阅读源码,读5遍左右(我就是读了5遍),应该可以完全理解了-:)。决策树是随机森林和梯度提升树的基础,理解了决策树,再看其他两种模型,都是可以秒懂的-:)。
参考引用
《Scalable Distributed Decision Trees in Spark MLlib》
《PLANET: Massively Parallel Learning of Tree Ensembles with MapReduce》
官方文档Decision Trees - spark.mllib