分割网络损失函数总结！交叉熵，Focal loss，Dice，iou，TverskyLoss！

---

前言

在实际训练分割网络任务过程中，损失函数的选择尤为重要。对于语义分割而言，极有可能存在着正负样本不均衡，或者说类别不平衡的问题，因此选择一个合适的损失函数对于模型收敛以及准确预测有着至关重要的作用。

---

一、交叉熵loss

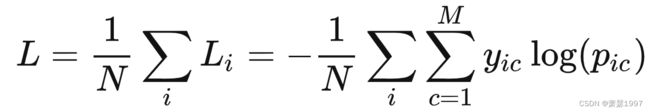
M为类别数；
yic为示性函数，指出该元素属于哪个类别；
pic为预测概率，观测样本属于类别c的预测概率，预测概率需要事先估计计算；

缺点：
交叉熵Loss可以用在大多数语义分割场景中，但它有一个明显的缺点，那就是对于只用分割前景和背景的时候，当前景像素的数量远远小于背景像素的数量时，即背景元素的数量远大于前景元素的数量，背景元素损失函数中的成分就会占据主导，使得模型严重偏向背景，导致模型训练预测效果不好。

同理BCEloss同样面临着这个问题，BCEloss如下。

对所有N个类别都做一次二分类损失计算。

  #二值交叉熵，这里输入要经过sigmoid处理
import torch
import torch.nn as nn
import torch.nn.functional as F
nn.BCELoss(F.sigmoid(input), target)
#多分类交叉熵, 用这个 loss 前面不需要加 Softmax 层
nn.CrossEntropyLoss(input, target)

---

二、Focal loss

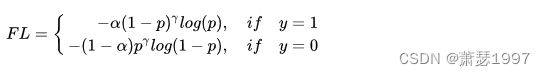
何凯明团队在RetinaNet论文中引入了Focal Loss来解决难易样本数量不平衡，我们来回顾一下。
对样本数和置信度做惩罚，认为大样本的损失权重和高置信度样本损失权重较低。

class FocalLoss(nn.Module):
   """
   copy from: https://github.com/Hsuxu/Loss_ToolBox-PyTorch/blob/master/FocalLoss/FocalLoss.py
   This is a implementation of Focal Loss with smooth label cross entropy supported which is proposed in
   'Focal Loss for Dense Object Detection. (https://arxiv.org/abs/1708.02002)'
       Focal_Loss= -1*alpha*(1-pt)*log(pt)
   :param num_class:
   :param alpha: (tensor) 3D or 4D the scalar factor for this criterion
   :param gamma: (float,double) gamma > 0 reduces the relative loss for well-classified examples (p>0.5) putting more
                   focus on hard misclassified example
   :param smooth: (float,double) smooth value when cross entropy
   :param balance_index: (int) balance class index, should be specific when alpha is float
   :param size_average: (bool, optional) By default, the losses are averaged over each loss element in the batch.
   """

   def __init__(self, apply_nonlin=None, alpha=None, gamma=2, balance_index=0, smooth=1e-5, size_average=True):
       super(FocalLoss, self).__init__()
       self.apply_nonlin = apply_nonlin
       self.alpha = alpha
       self.gamma = gamma
       self.balance_index = balance_index
       self.smooth = smooth
       self.size_average = size_average

       if self.smooth is not None:
           if self.smooth < 0 or self.smooth > 1.0:
               raise ValueError('smooth value should be in [0,1]')

   def forward(self, logit, target):
       if self.apply_nonlin is not None:
           logit = self.apply_nonlin(logit)
       num_class = logit.shape[1]

       if logit.dim() > 2:
           # N,C,d1,d2 -> N,C,m (m=d1*d2*...)
           logit = logit.view(logit.size(0), logit.size(1), -1)
           logit = logit.permute(0, 2, 1).contiguous()
           logit = logit.view(-1, logit.size(-1))
       target = torch.squeeze(target, 1)
       target = target.view(-1, 1)
       # print(logit.shape, target.shape)
       # 
       alpha = self.alpha

       if alpha is None:
           alpha = torch.ones(num_class, 1)
       elif isinstance(alpha, (list, np.ndarray)):
           assert len(alpha) == num_class
           alpha = torch.FloatTensor(alpha).view(num_class, 1)
           alpha = alpha / alpha.sum()
       elif isinstance(alpha, float):
           alpha = torch.ones(num_class, 1)
           alpha = alpha * (1 - self.alpha)
           alpha[self.balance_index] = self.alpha

       else:
           raise TypeError('Not support alpha type')
       
       if alpha.device != logit.device:
           alpha = alpha.to(logit.device)

       idx = target.cpu().long()

       one_hot_key = torch.FloatTensor(target.size(0), num_class).zero_()
       one_hot_key = one_hot_key.scatter_(1, idx, 1)
       if one_hot_key.device != logit.device:
           one_hot_key = one_hot_key.to(logit.device)

       if self.smooth:
           one_hot_key = torch.clamp(
               one_hot_key, self.smooth/(num_class-1), 1.0 - self.smooth)
       pt = (one_hot_key * logit).sum(1) + self.smooth
       logpt = pt.log()

       gamma = self.gamma

       alpha = alpha[idx]
       alpha = torch.squeeze(alpha)
       loss = -1 * alpha * torch.pow((1 - pt), gamma) * logpt

       if self.size_average:
           loss = loss.mean()
       else:
           loss = loss.sum()
       return loss

---

一、Dice损失函数

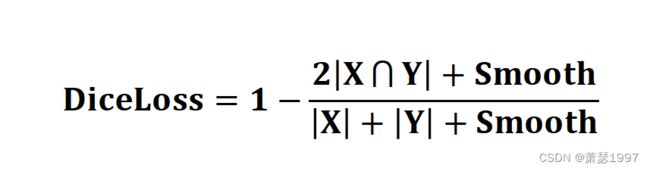
集合相似度度量函数。通常用于计算两个样本的相似度,属于metric learning。X为真实目标mask，Y为预测目标mask，我们总是希望X和Y交集尽可能大，占比尽可能大，但是loss需要逐渐变小，所以在比值前面添加负号。
可以缓解样本中前景背景（面积）不平衡带来的消极影响，前景背景不平衡也就是说图像中大部分区域是不包含目标的，只有一小部分区域包含目标。Dice Loss训练更关注对前景区域的挖掘，即保证有较低的FN，但会存在损失饱和问题，而CE Loss是平等地计算每个像素点的损失。因此单独使用Dice Loss往往并不能取得较好的结果，需要进行组合使用，比如Dice Loss+CE Loss或者Dice Loss+Focal Loss等。

该处说明原文链接：https://blog.csdn.net/Mike_honor/article/details/125871091

def dice_loss(prediction, target):
    """Calculating the dice loss
    Args:
        prediction = predicted image
        target = Targeted image
    Output:
        dice_loss"""

    smooth = 1.0

    i_flat = prediction.view(-1)
    t_flat = target.view(-1)

    intersection = (i_flat * t_flat).sum()

    return 1 - ((2. * intersection + smooth) / (i_flat.sum() + t_flat.sum() + smooth))

def calc_loss(prediction, target, bce_weight=0.5):
    """Calculating the loss and metrics
    Args:
        prediction = predicted image
        target = Targeted image
        metrics = Metrics printed
        bce_weight = 0.5 (default)
    Output:
        loss : dice loss of the epoch """
    bce = F.binary_cross_entropy_with_logits(prediction, target)
    prediction = F.sigmoid(prediction)
    dice = dice_loss(prediction, target)

    loss = bce * bce_weight + dice * (1 - bce_weight)

    return loss

---

一、IOU损失

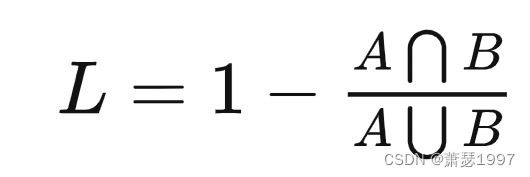
该损失函数与Dice损失函数类似，都是metric learning衡量，在实验中都可以尝试，在小目标分割收敛中有奇效！

def SoftIoULoss( pred, target):
        # Old One
        pred = torch.sigmoid(pred)
        smooth = 1

        # print("pred.shape: ", pred.shape)
        # print("target.shape: ", target.shape)

        intersection = pred * target
        loss = (intersection.sum() + smooth) / (pred.sum() + target.sum() -intersection.sum() + smooth)

        # loss = (intersection.sum(axis=(1, 2, 3)) + smooth) / \
        #        (pred.sum(axis=(1, 2, 3)) + target.sum(axis=(1, 2, 3))
        #         - intersection.sum(axis=(1, 2, 3)) + smooth)

        loss = 1 - loss.mean()
        # loss = (1 - loss).mean()

        return loss

---

一、TverskyLoss

分割任务也有不同侧重点，如医学分割更加关注召回率（高灵敏度），即真实mask尽可能都被预测出来，不太关注预测mask有没有多预测。B为真实mask,A为预测mask。|A-B|为假阳，|B-A|为假阴，alpha和beta可以控制假阳和假阴之间的权衡。若我们更加关注召回，则放大|B-A|的影响。

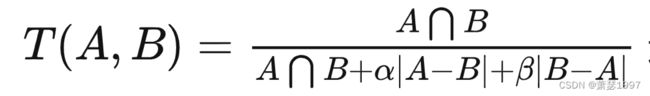
其中alpha和beta可以影响找回率和准确率，若想目标有较高的召回率，那么我们可以选择较高的beta。

class TverskyLoss(nn.Module):
   def __init__(self, apply_nonlin=None, batch_dice=False, do_bg=True, smooth=1.,
                square=False):
       """
       paper: https://arxiv.org/pdf/1706.05721.pdf
       """
       super(TverskyLoss, self).__init__()

       self.square = square
       self.do_bg = do_bg
       self.batch_dice = batch_dice
       self.apply_nonlin = apply_nonlin
       self.smooth = smooth
       self.alpha = 0.3
       self.beta = 0.7

   def forward(self, x, y, loss_mask=None):
       shp_x = x.shape

       if self.batch_dice:
           axes = [0] + list(range(2, len(shp_x)))
       else:
           axes = list(range(2, len(shp_x)))

       if self.apply_nonlin is not None:
           x = self.apply_nonlin(x)

       tp, fp, fn = get_tp_fp_fn(x, y, axes, loss_mask, self.square)


       tversky = (tp + self.smooth) / (tp + self.alpha*fp + self.beta*fn + self.smooth)

       if not self.do_bg:
           if self.batch_dice:
               tversky = tversky[1:]
           else:
               tversky = tversky[:, 1:]
       tversky = tversky.mean()

       return -tversky

---

总结

在经过一系列实验后，发现后四种损失函数更加适合小目标分割网络训练。但是每个任务都有差异，如果时间很充裕的话，可以挨个尝试一下。