java数据结构与算法(一)--排序
java数据结构与算法(一)排序算法
- 简单排序
-
- 冒泡排序
- 选择排序
- 插入排序
- 高级排序
-
- 希尔排序
- 归并排序
- 快速排序
引言:本文来自于黑马教程的总结与记录, 视频链接。学习数据结构与算法不要死记结果,而是分析问题,分析过程,动手实现,实现方式并不唯一,思想才是正解。
简单排序
冒泡排序
思路:

1.比较相邻的元素,如果前一个元素比后一个元素大,就交换两个元素的位置。
2.每一对比较完成后,最后一个数字就是最大值
3.每次比较的最后(0,1,2,3…)个数字已经比较完成,不需要再进行比较
方式一:
public class BubbleTest {
static int arr[] = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
//循环arr.length次,从索引0处开始
for (int i = 0; i < arr.length; i++) {
//内存循环比较,从0开始,每次比较[x]与[x+1]的值,并且内循环的次数需要减去已确定次数
for (int j = 0; j < arr.length - i-1; j++) {
if (arr[j]>arr[j+1]){
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
System.out.println(Arrays.toString(arr));
}
}
方式二:
public class BubbleTest {
static int arr[] = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
for(int i=arr.length-1; i>=0 ;i--){
for (int j=0; j<i ;j++){
if (arr[j]>arr[j+1]){
int temp=arr[j+1];
arr[j+1]=arr[j];
arr[j]=temp;
}
}
}
System.out.println(Arrays.toString(arr));
}
}
实现方法并不固定,解题思想是一致的。
选择排序
思路:
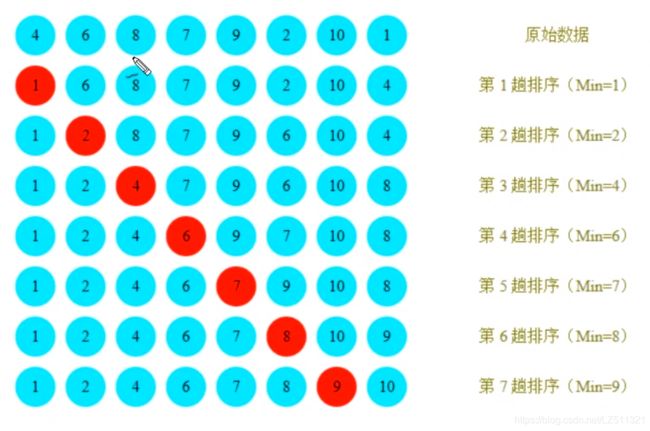
1.每一次遍历的过程中,都假定第一个索引处的元素是最小值,和其他索引处的值进行比较,如果当前索引处的值大于其他索引值,则假定其他索引值为最小值,最终可以找到最小值所在的索引
2.交换第一个索引处和最小值所在的索引处的值
3.每次循环都会确定出一个最小值
4.循环进行到最后一次时,当前索引一定为最小值,因此外层循环次数为数组长度-1次
public class SelectTest {
static int arr[] = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
for(int i=0; i<arr.length-1; i++){
int minIndex=i;
//默认第一个索引值为最小值,所以从i+1处开始比较
for(int j=i+1; j<arr.length;j++){
//发现假设索引值比当前循环索引值大时,将最小索引换成当前循环索引
if (arr[minIndex]>arr[j]){
minIndex=j;
}
}
//第一个索引值真的就是最小的值时,不再需要交换值
if (arr[minIndex]<arr[i]){
//交换最小索引值与索引起始值
int temp=arr[minIndex];
arr[minIndex]=arr[i];
arr[i]=temp;
}
}
System.out.println(Arrays.toString(arr));
}
}
插入排序
思路:
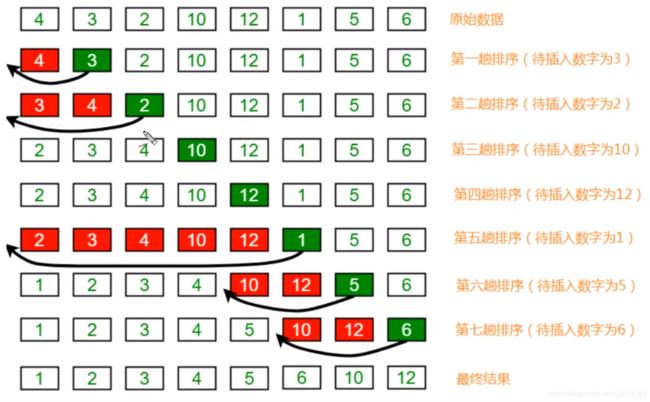
1.将元素分为两组,已排序和未排序
2.第一个元素默认为已排序,所以完成循环从1开始
3.内存循环进行倒序比较,当前值小于下一个值时,交换位置,当大于下一个值时,认为已经找到了插入地方,结束内循环,开始下一次外循环
public class InsertTest {
static int arr[] = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
//默认第一个为已排序数组,从1开始外循环
for (int i=1; i<arr.length; i++){
//倒序开始排列,j为待插入元素,j-1~0为已排序数组
for(int j=i; j>0; j--){
if (arr[j]<arr[j-1]){
//当前值小于下一个值,则交换位置
int temp=arr[j];
arr[j]=arr[j-1];
arr[j-1]=temp;
}else{
//找到了插入的地方,结束内循环
break;
}
}
}
System.out.println(Arrays.toString(arr));
}
}
以上排序算法,时间复杂度都是O(n^2) ,随着问题规模增长,时间消耗急剧增长。
高级排序
当数据量太多时,简单排序的时间复杂度是指数级增长,耗费时间过长,因此需要学习高级排序
希尔排序
思路:
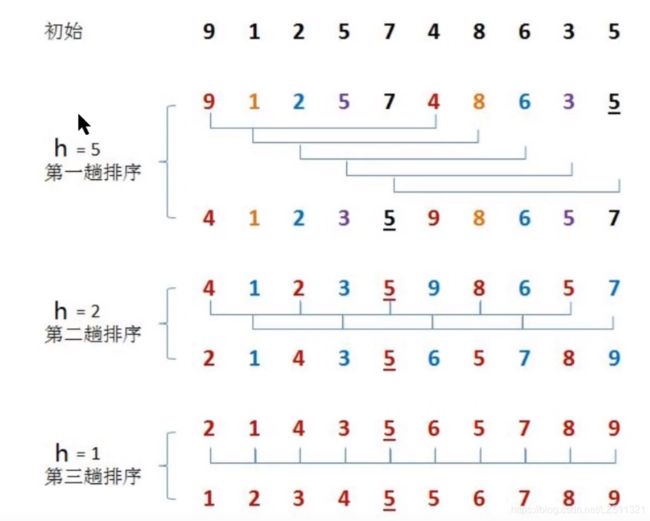
1.希尔排序其实可以看做插入排序的进阶版
2.选定一个增长量h,按照增长量h作为数据分组的依据,对数据进行分组(例如:h为5时。元数据被分为5组-[9,4],[1,8]…[7,5],h为5时,分为两组[4,2,5,8,5],[1,3,9,6,7])
3.对分组好的每一组数据完成插入排序
4.减小增长量,重新分组,然后完成插入排序,直到h变为1
public class ShellTest {
static int arr[] = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
//按增量循环,使用希尔增量,即arr.length/2定义为初始增量
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
//进行分组
for (int i = gap; i < arr.length; i++) {
//(gap=5,按gap分组为5,6,7,8,9,由图推断,下标5应和0为一组,6和1为一组。。。)
for (int j = i; j >= gap; j -= gap) {
//按照插入排序的思想,当待插入数据小于比较数据,则交换位置,否则认为找到了合适的位置,结束循环
if (arr[j] < arr[j - gap]) {
int temp = arr[j - gap];
arr[j - gap] = arr[j];
arr[j] = temp;
} else {
break;
}
}
}
}
System.out.println(Arrays.toString(arr));
}
}
对代码进行分析解释:
1.最外层for循环负责进行gap增长量的变换
2.内层两个for循环进行插入排序
3.以图中数据为例,当gap=5时,i取值范围为5,6,7,8,9,内层for循环比较内容为[5,0],[6,1],[7,2],[8,3],[9,4],按照插入排序,两组数据直接替换
4.当gap=2时,i的取值为2,3,4,5,6,7,8,9, 内层循环依次进行比较为[2,0],[3,1],[4,2,0],[5,3,1],…[8,6,4,2,0],[9,7,5,3,1],由此分析可发现 i取值为偶数时,数据可为一组,i取值为奇数时,数据为另一组,即[0,2,4,6,8] ,[1,3,5,7,9]这两组数据,然后对他们进行了插入排序
总结:希尔排序为插入排序的进阶版,宏观上分组调控,采用算法的事前分析法较为麻烦,且因为gap的取值问题,导致更难分析,因此采用事后分析法,以10w的逆序数据进行排序,并进行时间总结会发现希尔排序的时间消耗量远小于任何简单排序
事后分析:
希尔排序耗时:结果为10~15毫秒
public class ShellTest {
static Integer arr[];
static ArrayList<Integer> arrayList=new ArrayList<>();
public static void main(String[] args) {
for (int i=100000; i>=0 ;i--){
arrayList.add(i);
}
arr= arrayList.toArray(new Integer[]{});
long startTime=System.currentTimeMillis();
//按增量循环,使用希尔增量,即arr.length/2定义为初始增量
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
//进行分组
for (int i = gap; i < arr.length; i++) {
//(gap=5,按gap分组为5,6,7,8,9,由图推断,下标5应和0为一组,6和1为一组。。。)
for (int j = i; j >= gap; j -= gap) {
//按照插入排序的思想,当待插入数据小于比较数据,则交换位置,否则认为找到了合适的位置,结束循环
if (arr[j] < arr[j - gap]) {
int temp = arr[j - gap];
arr[j - gap] = arr[j];
arr[j] = temp;
} else {
break;
}
}
}
}
System.out.println(System.currentTimeMillis()-startTime);
System.out.println(Arrays.toString(arr));
}
}
插入排序耗时:用同样的数据进行分析,结果为21528毫秒
归并排序
思路:
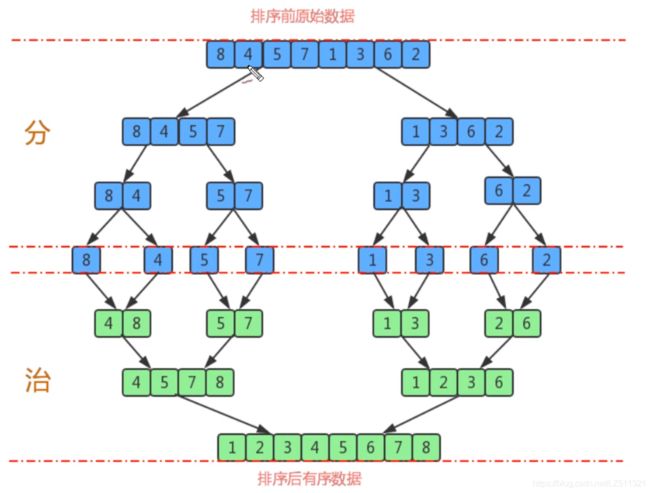
1.尽可能的将一个数组分为两个元素相等的子组,并对子组继续进行拆分,直到拆分后每个子元组的元素个数是1为止
2,将相邻的两个子组进行合并,成为一个有序的大组
3.不断重复2步骤
前排提示:归并排序较为复杂,看不懂的话,可以去看一看视频,讲解的更清楚
public class MergeTest {
//辅助数组
static Integer arrs[]={10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static Integer[] assist=new Integer[arrs.length];
public static void main(String[] args) {
long startTime=System.currentTimeMillis();
//归并开始
grouping(arrs, 0, arrs.length - 1);
System.out.println(System.currentTimeMillis()-startTime);
// System.out.println(Arrays.toString(arrs));
}
//对数据进行分组
public static void grouping(Integer[] a, int start, int end) {
//递归终止条件
if (start >= end) {
return;
}
//寻找中间值
int mid = start + (end - start) / 2;
//进行递归分组
grouping(a, start, mid);
grouping(a, mid + 1, end);
//分组完毕,递归出栈,进行合并
merge(a, start, mid, end);
}
public static void merge(Integer[] a, int start, int mid, int end) {
int pAssist = start;
int pLeft = start;
int pRight = mid + 1;
//左组的指针执行区间为start-mid,右组为mid+1-end
while (pLeft <= mid && pRight <= end) {
if (a[pLeft] < a[pRight]) {
assist[pAssist++] = a[pLeft++];
} else {
assist[pAssist++] = a[pRight++];
}
}
//存在一组指针已经走到某尾,而另一侧指针未走完的情况,因此将剩余值直接放入辅助数组中
while (pLeft <= mid) {
assist[pAssist++] = a[pLeft++];
}
while (pRight <= end) {
assist[pAssist++] = a[pRight++];
}
//辅助数组中的值已排序,重新放入初始数组中
for (int i = start; i <= end; i++) {
a[i] = assist[i];
}
}
}
对代码进行分析解释:
1.归并采用递归的方式进行,因此需要先设置一个终止条件,即分组的开始索引必须小于结束索引
2.对一个数组分组,可以从数组中间的索引开始,则中间位置的索引为mid=start+(end-start)/2,数组是奇数还是偶数都没有关系,尽可能的分组就好
3.一个数组分为两个,则分别为[start,mid] ,[mid+1,end],继续对这两个数组分组,直到数组中只有一个元素为止
4.当分组完成后,虚拟机栈的方法帧开始出栈,进行合并运算,即代码中的merge方法
打印日志对递归分组进行分析
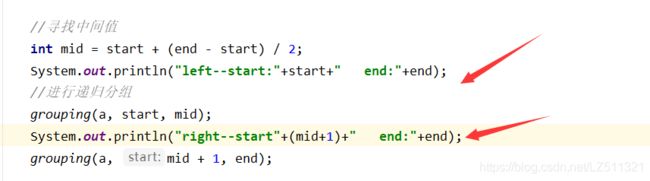
得出结果:

对结果进行分析,按grouping调用进行说明,此处只说明start与end两个变量
(1).首先是group方法中,第一次调用自己,每次对数组分割的起始为start->mid,理解为数组的左半部分,即:
group(0,9) ->group(0,4)->group(0,2)->group(0,1) -> group(0,0) 最后一个满足start>=end,因此return。
(2).group方法第二次调用自己,每次对数组分割起始为mid+1->end,理解为数组的右半部分,由于栈的特性(先入后出,后入先出),因此第二次调用group方法时的start、mid、end应该为第一次方法栈调用的逆序,即:
group(1,1) ->满足start>=end,则方法进行下一步调用一次归并方法
group(2,2)->满足start>=end,则方法进行下一步调用一次归并方法
group(3,4)->因为不满足start>=end,因此会再次进入方法循环,即在方法中的第一次调用自己处会再调用一次自己,反应在结果出也就是left --start:3 end:4
依照递归的方法,即可完成对所有的数据分组
5.合并排序算法
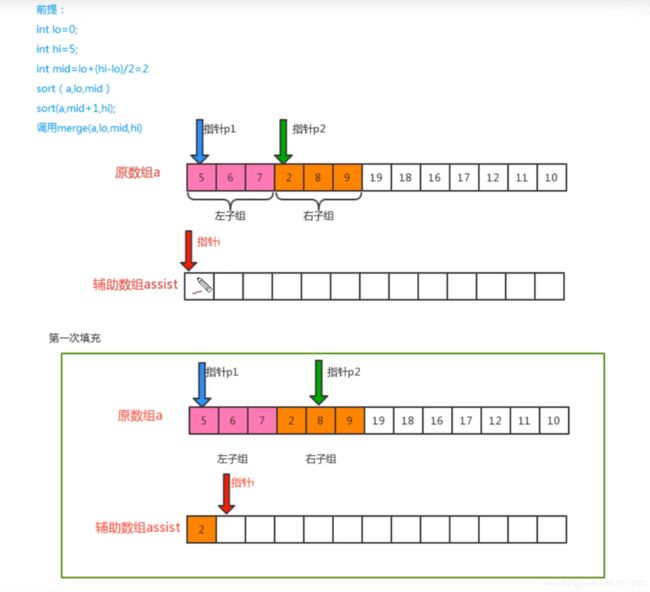
(1)传入的数组,依靠mid中间量,分为左右两个数组,并分别按照指针进行大小比较,值小的放入辅助数组中,并将小的指针位置进行后移,当有一个全部移动完成后终止循环,并将数组剩余填充到辅助数组中,最后将辅助数组的值覆盖到原数组中
(2)从宏观上来说,因为两个组都是从最小的分组开始排列,因此左右两个数组在自己的范围内总是有序的,因此可以进行这样的比较。
总结:归并排序因为需要使用一个辅助数组来进行排序,并且递归意味着虚拟机栈内将会大量的存储方法帧,当数量过多时,存在OOM和栈溢出的风险,是典型的用空间来减少时间复杂度的算法。
后排提示:看不懂的还是去看看视频吧
快速排序
思路:

1.快速排序算法采用分治法,不同于归并排序,它没有合并的过程
2. 采用数组的第一个元素值作为分界值,遍历数组,将比分界值小的元素放在左边,比元素小的放在右边
3. 将数组从分界值分为左右两个组,再分别对它们进行步骤2的操作
public class QuickTest {
static int[] arrs = {10, 5, 6, 8, 9, 7, 3, 4, 1, 2};
public static void main(String[] args) {
sort(arrs, 0, arrs.length - 1);
System.out.println(Arrays.toString(arrs));
}
public static void sort(int[] a, int start, int end) {
if (start >= end) {
return;
}
//拿到处理后的分界值,分界值左边全比它小,右边全比它大
int par = partition(a, start, end);
//继续处理分开的左边的数组
sort(a, start, par - 1);
//继续处理分开的右边的数组
sort(a, par + 1, end);
}
//返回分界值对应的索引
public static int partition(int[] a, int start, int end) {
//以数组第一个值为界限值,
int splitNum = a[start];
//在剩余的数组start-end中,将值小于界限值的放在左边,值大于界限值的放在右边,使用left与right作为指针
int left = start;
int right = end + 1;
while (left < right) {
//先从right开始,当找到一个值比分界值小的元素,停止
while (splitNum < a[--right] && left < right) {
//意味着右指针指向了头索引也没有找到合适的值,则停止循环
if (right == start) {
break;
}
}
//从left开始,当找到一个值比分界值大的元素,停止
while (splitNum > a[++left] && left < right) {
//意味着左指针指向了尾索引也没有找到合适的值,则停止循环
if (left == end) {
break;
}
}
//当左指针依旧小于右指针时,交换两个指针指向的值,目的是为了让左侧的值上小于右侧
if (left < right) {
int temp = a[left];
a[left] = a[right];
a[right] = temp;
}
}
//排序完成,最终交换start与right的值,因right向左侧的值全部小于a[start]界限值,right向右侧的值,全部大于a[start]
//并且将right最终指向的值一定是比a[start]小的,交换a[start]与a[right]则实现分组排序,且right就是处理后分界值的索引
int temp = a[start];
a[start] = a[right];
a[right] = temp;
return right;
}
}
代码解释:
1.sort方法中,首先去对当前数组进行排序,将分界值左侧的分割为一个数组(左侧的值比分界值小),将分界值右侧的分割为一个数组(右侧的值比分界值的大),然后进行递归
2.partition方法解析 :
(1).以数组a={5, 6, 8, 9, 7, 3, 4, 1, 2}为例,数组第一个值设定为分界值,即splitNum=a[0]=5;
(2).定义两个指针,一个left指向5的位置(start),一个right指向a.length的位置(end+1),即需要对{6, 8, 9, 7, 3, 4, 1, 2}数组进行遍历排序,将比5大的元素放在数组右边,比5小的元素放在数组左边
(3).进入while循环,当left>=right时,代表数组遍历完毕,终止循环
(4).首先让right指针开始递减,寻找比分界值5小的元素(比5大的元素在右侧,不需要动位置),然后让left指针开始递加,寻找比分界值5大的元素(比5小的元素在左侧,不需要动位置),当完成一次寻找后,交换left指针与right指针指向的值,即完成了一次比5小的值和比5大的值的排序。
(5).当left指针与right指针交错时,停止遍历,此时将原先5与right指针最后一次指向的值进行互换,则完成了将分界值放在合适的地方(它左侧的值小于它,它右侧的值大于它),且right指针就为最终分界值5所在的索引
调用partitiond方法对数组{5, 6, 8, 9, 7, 3, 4, 1, 2}处理,进行过程跟踪以证明思路:

①.–right=2,小于5,停止right指针移动,++left=6,大于5,停止left指针移动,此时left为1,right为8,交换a[1]=6与a[8]=2,得到数组{5,2,8,7,3,4,1,6}
…
②.当指针移动完成后,right指针此时为4,交换初始值与right指向的值,得到{3,2,1,4,5,7,8,6},可以观察到,5左侧的值都小于它,右侧的值都大于它,且5的索引为right的值4
以上实现方式,便于理解,还有更多的优化版实现方式,感兴趣的可自行百度。