读《贝叶斯的博弈》1-7章

贝叶斯定理不再是一套枯燥的数学理论或认识论，他变成可应用广泛。无所不及的知识宝库，催生了众多数学定理以及令人称道的实践成果。

上面是翻译者对于本书的评价，我在看本书之前，大学期间学习概率论和机器学习课程的时候对贝叶斯定理有一定的了解，公式的简洁让我觉得贝叶斯定理不过是概率中注入条件概率、全概率公式的应用，开始读这本书后我才对贝叶斯定理有了更深刻的理解。贝叶斯主义知识哲学，是我从这本书学习接触到的。

第一章 初始

两个有趣的例子，解释了贝叶斯定理存在与否带来不一样的结果。小男孩和克拉克审判，现在看来可以使用贝叶斯定理清晰算出概率，做出正确答案。未曾想到，如果没有贝叶斯定理，答案很有可能走向另一个方向。

作者黄黎原(输入法竟然没有弹出词条)在本章极力地表现了对贝叶斯主义的热情，能够看出作者在学习贝叶斯主义时所获得的收获和这种哲学上通透开朗的喜悦。对真理的追求，是科研工作者的底色。

统一的知识哲学，贝叶斯主义的定义：第一，任何理论都是错误的，众多理论是一种诗歌、幻想；第二，实际数据体现理论的置信度；第三，调整置信度要通过贝叶斯公式。

第二章 贝叶斯定理

这章主要讲贝叶斯定理，结合了第一章的例子，给出了贝叶斯定理运用计算过程。

贝叶斯定理 由英国数学家贝叶斯 (Thomas Bayes 1702-1761) 发展，用来描述两个条件 概率 之间的关系，比如 P (A|B) 和 P (B|A)。 按照乘法法则，可以立刻导出：P (A∩B) = P (A)*P (B|A)=P (B)*P (A|B)。 如上公式也可变形为：P (A|B)=P (B|A)*P (A)/P (B)

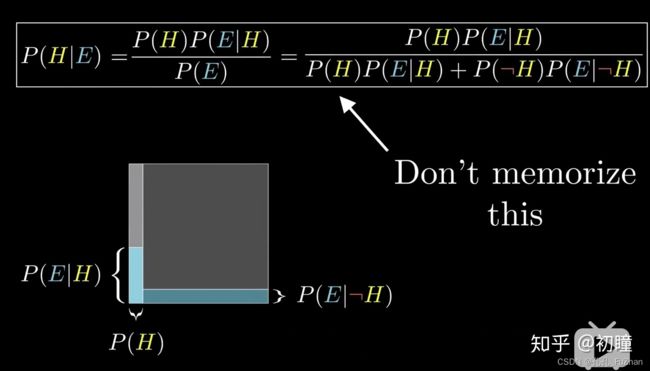简单的公式，留给了很大的应用空间。脱离概率论课堂，用哲学眼光来看待这个公式便会发现这个公式的美妙之处：在现有数据（data or situation），在做决策的语境下（选择、赌局），如何计算概率做出决策？

贝叶斯定理给出答案：近似计算先验概率P（H），全概率公式P(E)，以及后验概率P(E|H)。白话说，从历史中找经验。

但是这种历史并不是单纯的频率主义。

按照考研成功率来讲，严格的频率主义者会这样预测，拿到今年的报考人数以及预测的录取人数，这样就算得自己被录取的概率。

这样非常简单粗暴，实用贝叶斯主义者会不屑一顾。换做是贝叶斯主义者，除了考虑这些，还会考虑其他更多因素。也就是思考更多思考实验项，比如P(报考|性别=“男”)，P(报考|地域=“北京”)。P(上岸|今年) 会考虑先验概率P(上岸)，后验概率P(今年|上岸)，以及众多思想实验项组成的P(今年)。
感觉“今年”这个并不是多么合适，改成P(今年考研情况)。

（这是我对频率主义的偏见，读这本书已经让我对贝叶斯定理更有好感，也对频率主义的置信度下降。当然，我认为频率主义也有用武之地，我举的例子也非常不恰当，只是为了说明频率主义会失灵。）

得到一些看起来朴素又通过贝叶斯定理加深的道理：信息（也就是数据）是做决策所必要的。从第五章还可以得出更多的结论：对数据的偏见也是贝叶斯主义者做决策所需要的。

“从不害怕暴露偏见”

第三章 从逻辑上来说

没什么好写的，布尔变量、逻辑量词、蕴含关系之类的内容。离散数学中学习到过。其中最难理解的，逆否命题和原命题的真值相同，当时大一初学觉得非常难懂，现在来看也易如反掌了。（可见认知是在递进的）

第四章 必须正确泛化

没太理解泛化的含义（机器学习小白），先给出一段定义。
定义来源：深入理解泛化

机器学习（深度学习）的根本问题是优化和泛化之间的对立。
优化（optimization）是指调节模型以在训练数据上得到最佳性能（即机器学习中的学习），而泛化（generalization）是指训练好的模型在前所未见的数据上的性能好坏。

所以这里的泛化是指，在已知道的模型或者定理（比如牛顿运动定律），面对新数据，应该正确泛化，也就是应该按照模型对新数据做出预测的方法应该是科学且正确的。

这一章的内容逻辑性不强，我看到的前七章逻辑性都不强，比较诟病的一点

始终没太理解波普尔的可证伪性原则 的字面解释，给段定义吧

波普尔提出的Falsifiability被译为“可证伪性”。什么是伪？伪装吗？这个词语在字面上不太好理解。

张五常在《经济解释》中用了一章来说明，被陈述为：

“可能被事实推翻”。

一个科学的理论、假说，要做到“可能被事实推翻”，这说的就很到位。

现在明白了，可证伪性是这个意思。

频率主义哲学的核心p值

这个p值就是在数理统计当中学习到的p值

关于P值，教科书会告诉你“它是在零假设成立的条件下，出现统计量目前值及更不利于零假设数值的概率。也就是当零假设成立时，我们凭借样本中所见去拒绝零假设（下阳性结论），有可能犯假阳性错误，犯假阳性错误的概率就是P。当P值较小，表明“不大可能”犯假阳性错误，于是拒绝零假设”。

而在这一章节，贝叶斯主义者通过实例证明频率主义也会犯很荒谬的错误，比如xkcd的太阳。

真的是精彩，我到现在才把概率论中学习到的p值和书中的p值联系起来，跟我学习到的东西联系起来了。

这篇博客先更新到这里，要去吃饭。