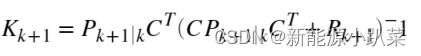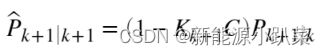基于自适应扩展卡尔曼滤波器（AEKF）的锂离子电池SOC估计（附MATLAB代码）

AEKF_SOC_Estimation函数使用二阶RC等效电路模型（ECM）和自适应扩展卡尔曼滤波器（AEKF）估计电池的端电压（Vt）和充电状态（SOC）。该函数将以下内容作为输入： 

· 电流(A)
· 电压(V)
· 温度(℃)

该函数的输出为：

· 估计SOC

· 估计电压Vt

· 电压Vt误差

function [SOC_Estimated, Vt_Estimated, Vt_Error] =AEKF_SOC_Estimation(Current, Vt_Actual, Temperature)

加载电池模型参数以及不同温度的SOC-OCV关系数据库。如果没有可用的温度数据或使用单一温度，建议使用25℃作为参考。用户应调整变量Cn，即在特定温度下的最大测量容量。 

默认情况下，该函数加载提供的“BatteryModel\_Sample”.mat’文件，它是一个带标签的表格。该表分别在第1列至第7列中包含OCV、SOC、、R0、R1、C1、R2、C2数据。SOC的范围为0%至100%，间隔约为10%，但用户可以根据需要增加或减少SOC。

load 'BatteryModel.mat'; % Load the battery parameters and SOC-OCV
curve

SOC-OCV曲线由电池单元的脉冲特性测试产生。通常这是C/20放电和充电测试，每个放电和充电曲线的平均值为每个温度的一个SOC-OCV。重要的是确保没有重复的SOC点（特别是如果这些点具有不同的OCV值），因为这将在函数运行时导致插值错误。通过HPPC或其他特性测试，使用Simulink和Simscape模拟对电池进行建模，以估计电池参数，其他可用方法包括优化算法，如GA遗传算法。T是在表征在驾驶循环测试时测得的电池温度。 

1.建模电池参数初始化

将初始SOC设置在0和1之间，其中0为0%，1为100%。可以将其设置为行驶循环初始SOC，或者设置为小于20%左右的值，以测试收敛性和鲁棒性。ΔT是电流矢量和Vt矢量中每个值之间的时间差，用于计算A和B矩阵。 

SOC_Init = 1; % intial SOC
X = [SOC_Init; 0; 0]; % state space x parameter intializations
DeltaT = 1; % sample time in seconds
Qn_rated = 4.81 * 3600; % Ah
% initialize scatteredInterpolant functions for battery parameters and
SOC-OCV curve
% this function also allows for extrapolation
F_R0 = scatteredInterpolant(param.T,param.SOC,param.R0);
F_R1 = scatteredInterpolant(param.T,param.SOC,param.R1);
F_R2 = scatteredInterpolant(param.T,param.SOC,param.R2);
F_C1 = scatteredInterpolant(param.T,param.SOC,param.C1);
F_C2 = scatteredInterpolant(param.T,param.SOC,param.C2);
F_OCV = scatteredInterpolant(param.T,param.SOC,param.OCV);

卡尔曼滤波器有3个参数可以调节：R、P和Q。这些参数需要手动或通过优化算法对每个电池进行调整/调谐。R应设置为用于测试电池单元的设备的误差的平方。一旦调整了Q的值，就不能更新R。 

n_x = size(X,1);
R_x = 2.5e-5;
P_x = diag(1e-10);
Q_x = [1.0000e-10 0 0;
0 1.0000e-10 0;
0 0 1.0000e-10];

初始化输出向量，并根据当前向量的大小设置for循环的长度。取消注释第25行，以测试0.1A的电流偏移。根据需要更新偏移。 

SOC_Estimated = [];
Vt_Estimated = [];
Vt_Error = [];
ik = length(Current);
% Current = Current+0.1;

2.卡尔曼滤波算法

这是自适应扩展卡尔曼滤波算法的开始。 循环基于当前输入电流数据长度。

for k=1:1:ik
T = Temperature(k); % C
U = Current(k); % A
SOC = X(1);
V1 = X(2);
V2 = X(3);
% Evaluate the battery parameter scatteredInterpolant
% functions for the current temperature & SOC
R0 = F_R0(T,SOC);
R1 = F_R1(T,SOC);
R2 = F_R2(T,SOC);
C1 = F_C1(T,SOC);
C2 = F_C2(T,SOC);
OCV = F_OCV(T,SOC);
% OCV = pchip(param.SOC,param.OCV,SOC); % pchip sample for unknown or
single temperature
The following is used to calculate the A and B matrices below on line 66 and 69.
Tao_1 = C1 * R1;
Tao_2 = C2 * R2;
a1 = exp(-DeltaT/Tao_1);
a2 = exp(-DeltaT/Tao_2);
b1 = R1 * (1 - exp(-DeltaT/Tao_1));
b2 = R2 * (1 - exp(-DeltaT/Tao_2));

3.运行更新模型

Vt方程基于：

TerminalVoltage = OCV - R0*U - V1 - V2;

当U（电流）为正时，电池正在放电，库仑效率（η）设置为0.99。当U（电压）为负时，电池在充电，库仑系数（η）。 

if U > 0
eta = 0.99; % eta for discharging
elseif U <= 0
eta = 1; % eta for charging
end

通过线性化C矩阵来线性化模型。该函数使用线性插值在特定查询点返回一维函数的插值。 

OCV = interp1(param.SOC,param.OCV,SOC,'linear','extrap');
C_x = [OCV -1 -1];
Calculate the Vt error.
Error_x = Vt_Actual(k) - TerminalVoltage;
if abs(Error_x) < 0.01
Error_x = 0.000;
end

保存/更新带有Vt误差的矢量中的SOC和电压估计值。这些是函数的输出向量。 

Vt_Estimated = [Vt_Estimated;TerminalVoltage];
SOC_Estimated = [SOC_Estimated;X(1)];
Vt_Error = [Vt_Error;Error_x];

4.EKF

EKF使用两步预测校正算法。使用上述变量计算A和B矩阵： 

 接下来，完成KF的预测（时间更新）部分。 

1.预测未来状态（先验）：

 2.预测误差协方差：

A = [1 0 0;
0 a1 0;
0 0 a2];
B = [-(eta * DeltaT/Qn_rated); b1; b2];
X = (A * X) + (B * U);
P_x = (A * P_x * A') + Q_x;

接下来，完成KF的校正（测量更新）部分。

1.计算卡尔曼增益：

 2.用测量值更新估计值Zk（后验）：

 3.更新误差协方差：

KalmanGain_x = (P_x) * (C_x') * (inv((C_x * P_x * C_x') + (R_x)));
X = X + (KalmanGain_x * Error_x);
P_x = (eye(n_x,n_x) - (KalmanGain_x * C_x)) * P_x;

5.自适应律协方差匹配（AEKF）

自适应律协方差匹配由下式给出： 

Q_x = KalmanGain_x * Error_x * KalmanGain_x';
end

6.下面给出自适应扩展卡尔曼滤波的绘图程序及结果：

% Terminal Voltage Measured vs. Estimated
figure
plot(LiPoly.RecordingTime_Hours,LiPoly.Measured_Voltage);
hold on
plot(LiPoly.RecordingTime_Hours,Vt_Estimated);
hold off;
legend('Measured','Estimated AEKF');
ylabel('Terminal Voltage[V]');xlabel('Time[hr]');
title('Measured vs. Estimated Terminal Voltage (V) at 40 Deg C')
grid minor
% Terminal Voltage Error
figure
plot(LiPoly.RecordingTime_Hours,Vt_Error);
legend('Terminal Voltage Error');
ylabel('Terminal Voltage Error');
xlabel('Time[hr]');
% SOC Coulomb Counting vs. Estimated
figure
plot (LiPoly.RecordingTime_Hours,LiPoly.Measured_SOC);
hold on
plot (LiPoly.RecordingTime_Hours,SOC_Estimated*100);
hold off;
legend('Coulomb Counting','Estimated AEKF');
ylabel('SOC[%]');xlabel('Time[hr]');
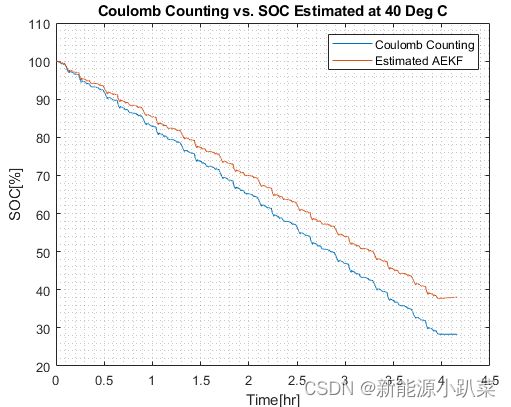
title('Coulomb Counting vs. SOC Estimated at 40 Deg C')
grid minor
% SOC Error
figure
plot(LiPoly.RecordingTime_Hours,(LiPoly.Measured_SOC - SOC_Estimated*100));
legend('SOC Error');
ylabel('SOC Error [%]');
xlabel('Time[hr]');
grid minor

1.仿真电压对比

 2.仿真电压误差

 3.SOC对比

 4.SOC误差